Содержание
- 2. Пример
- 3. Пример
- 4. Пример λ – собственное значение А ⬄
- 5. Пример λ – собственное значение А ⬄
- 6. Пример Канонический вид квадратичной формы: Собственные значения матрицы А: λ – собственное значение А ⬄
- 7. Пример Канонический вид квадратичной формы: Собственные значения матрицы А: λ – собственное значение А ⬄
- 10. – ФСР ОСЛУ свободные неизвестные)
- 11. где – ФСР ОСЛУ свободные неизвестные) Общий вид собственного вектора матрицы А при собственном значении
- 12. где – ФСР ОСЛУ свободные неизвестные) Выбранные векторы неортогональны, а нам нужен ортонормированный базис из собственных
- 13. Можно применить процесс ортогонализации:
- 14. Можно применить процесс ортогонализации:
- 15. Можно применить процесс ортогонализации: Нормируя эти векторы, получим первые два вектора искомого ортонормированного базиса:
- 16. Можно применить процесс ортогонализации: Нормируя эти векторы, получим первые два вектора искомого ортонормированного базиса: Третий вектор
- 17. Можно применить процесс ортогонализации: Нормируя эти векторы, получим первые два вектора искомого ортонормированного базиса: Третий вектор
- 18. ~ ~ С.з.
- 19. ~ ~ С.з. ~
- 20. ~ ~ С.з. ~ ~ ~
- 21. ~ ~ С.з. ~ ~ ~ Вектор – ФСР ОСЛУ
- 22. ~ ~ С.з. ~ ~ ~ Вектор – ФСР ОСЛУ ‒ единичный собственный вектор матрицы А
- 23. единичные собственные векторы матрицы А: Столбцами искомой ортогональной матрицы перехода Q (матрицы замены переменных) служат найденные
- 24. единичные собственные векторы матрицы А: Столбцами искомой ортогональной матрицы перехода Q (матрицы замены переменных) служат найденные
- 25. единичные собственные векторы матрицы А: Столбцами искомой ортогональной матрицы перехода Q (матрицы замены переменных) служат найденные
- 26. единичные собственные векторы матрицы А: Столбцами искомой ортогональной матрицы перехода Q (матрицы замены переменных) служат найденные
- 27. 34. Кривые второго порядка
- 28. 34.1. Общее уравнение – прямоугольная декартова система координат 34. Кривые второго порядка
- 29. 34.1. Общее уравнение Кривой второго порядка называется множество точек плоскости, задаваемое уравнением – прямоугольная декартова система
- 30. 34.1. Общее уравнение Кривой второго порядка называется множество точек плоскости, задаваемое уравнением – прямоугольная декартова система
- 32. выбирая на плоскости новый базис
- 33. выбирая на плоскости новый базис
- 34. квадратичной формы φ, выбирая на плоскости новый базис -- собственные векторы матрицы соответствующие собственным значениям λ1
- 35. Выбирая, если нужно, новое начало координат, 34.3. − заменой переменных
- 36. уравнение кривой приводят к каноническому виду − одному из девяти: Выбирая, если нужно, новое начало координат,
- 37. уравнение кривой приводят к каноническому виду − одному из девяти: Выбирая, если нужно, новое начало координат,
- 38. уравнение кривой приводят к каноническому виду − одному из девяти: Выбирая, если нужно, новое начало координат,
- 39. уравнение кривой приводят к каноническому виду − одному из девяти: Выбирая, если нужно, новое начало координат,
- 40. − пара действительных (−) мнимых (+) − пара совпавших прямых. − пара параллельных прямых действительных (+)
- 41. − пара 4) 5) пересекающихся прямых
- 42. − пара действительных (−) мнимых (+) 4) 5) пересекающихся прямых
- 43. − пара действительных (−) мнимых (+) 4) 5) 1−5 − уравнения центральных кривых второго порядка. пересекающихся
- 44. − пара действительных (−) мнимых (+) 4) 5) − парабола (p > 0); 6) 1−5 −
- 45. − пара действительных (−) мнимых (+) − пара параллельных прямых 4) 5) 7) 8) − парабола
- 46. − пара действительных (−) мнимых (+) − пара параллельных прямых действительных (+) мнимых (−) 4) 5)
- 47. − пара действительных (−) мнимых (+) − пара совпавших прямых. − пара параллельных прямых действительных (+)
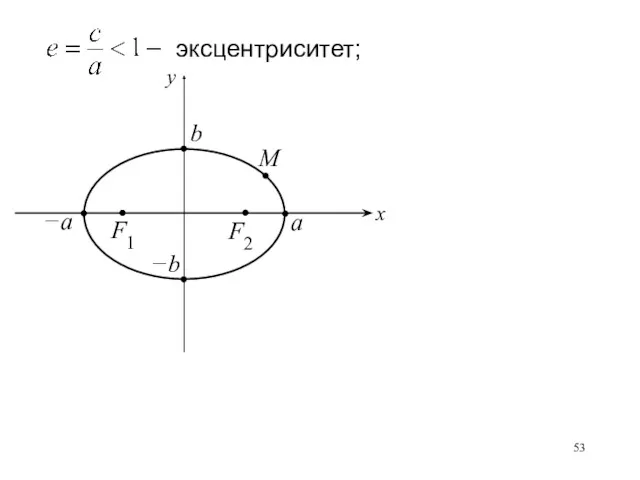
- 49. М (х; у) полуоси
- 50. М (х; у) полуоси (при a = b − окружность радиуса a);
- 51. М (х; у) полуоси фокусы; (при a = b − окружность радиуса a);
- 52. М (х; у) полуоси фокусы; (при a = b − окружность радиуса a);
- 53. эксцентриситет;
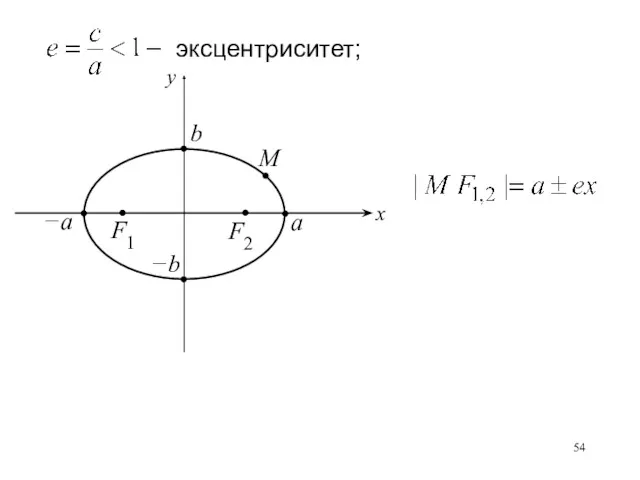
- 54. эксцентриситет;
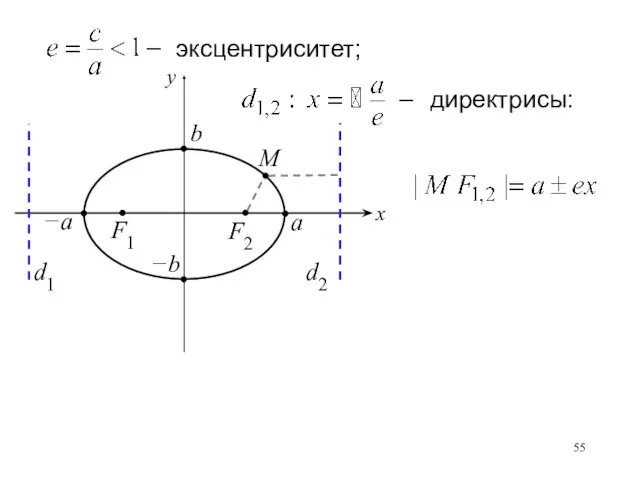
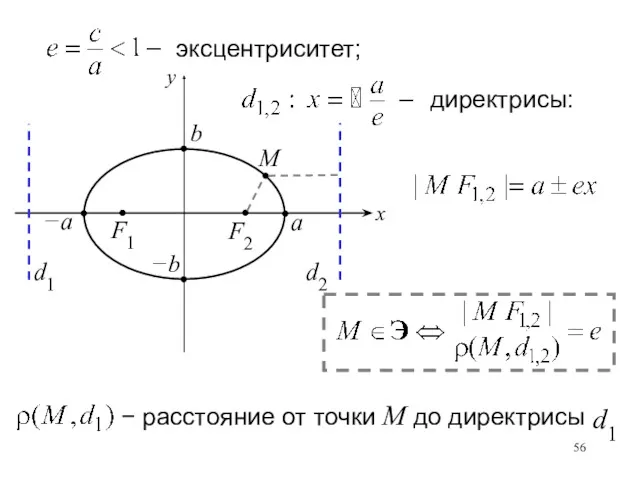
- 55. директрисы: эксцентриситет;
- 56. директрисы: эксцентриситет; − расстояние от точки М до директрисы d1
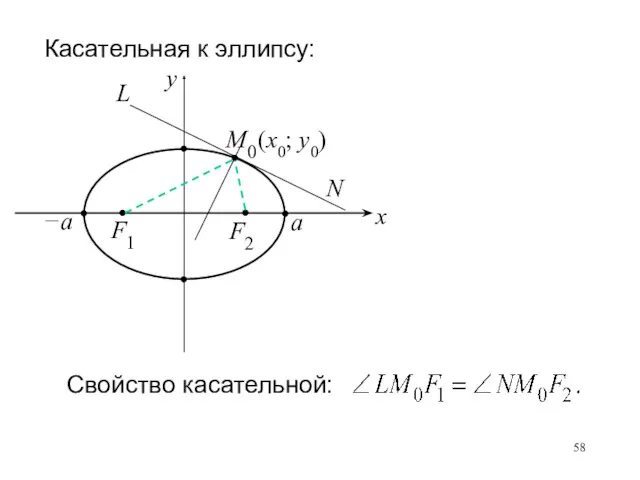
- 57. Касательная к эллипсу:
- 58. Свойство касательной: Касательная к эллипсу:
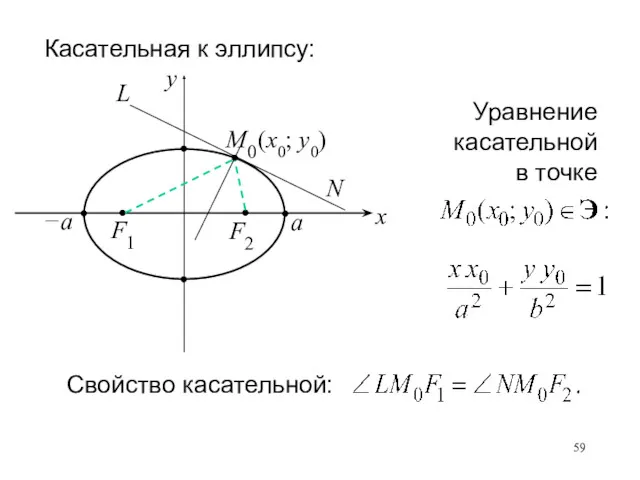
- 59. Уравнение касательной в точке Свойство касательной: Касательная к эллипсу:
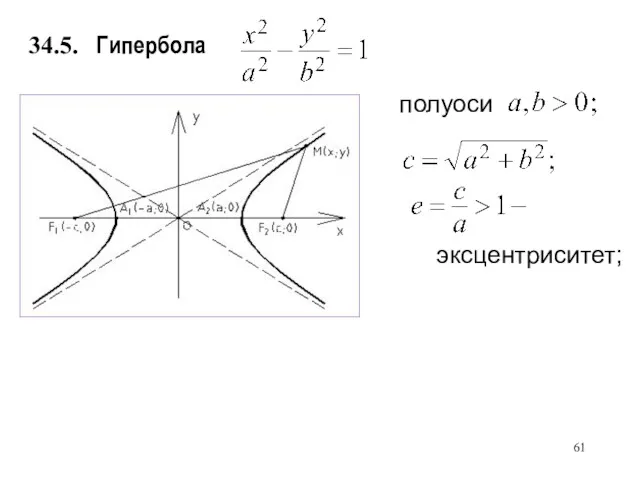
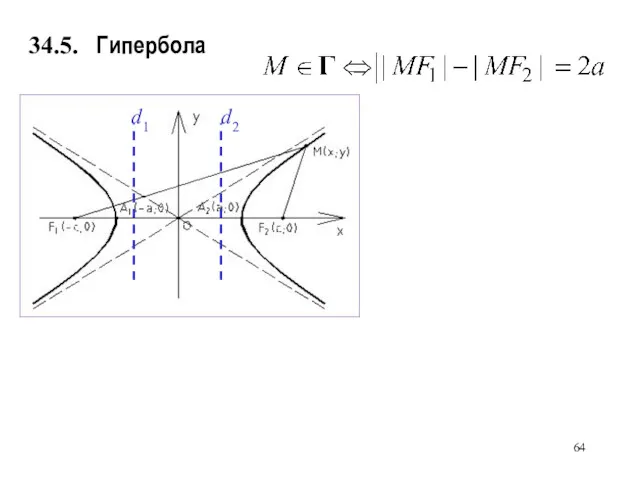
- 60. Гипербола 34.5. полуоси
- 61. Гипербола 34.5. полуоси эксцентриситет;
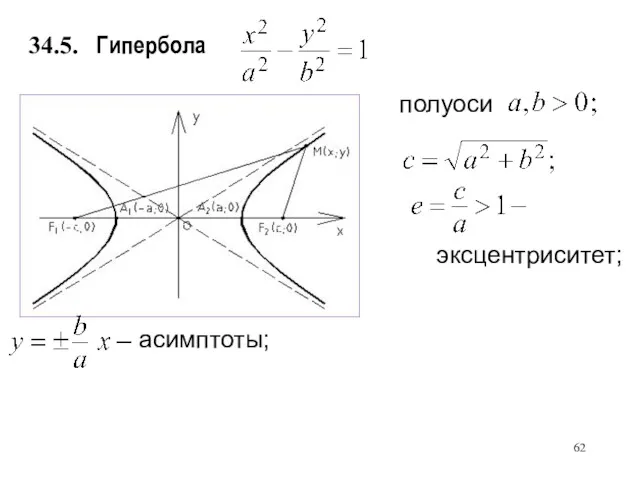
- 62. Гипербола 34.5. полуоси эксцентриситет; асимптоты;
- 63. Гипербола 34.5. полуоси фокусы; эксцентриситет; директрисы: асимптоты;
- 64. Гипербола d1 d2 34.5.
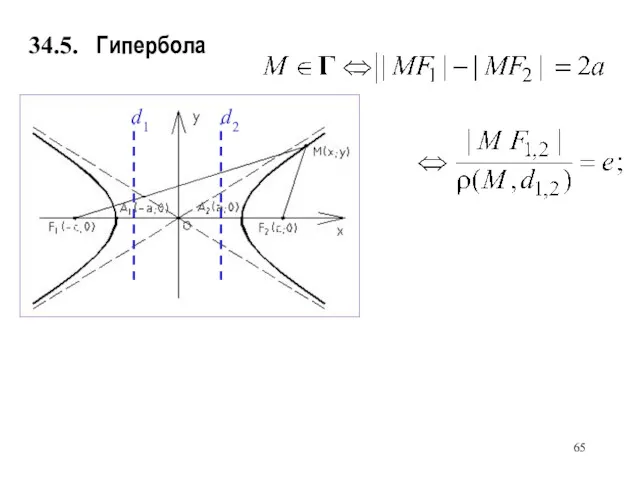
- 65. Гипербола d1 d2 34.5.
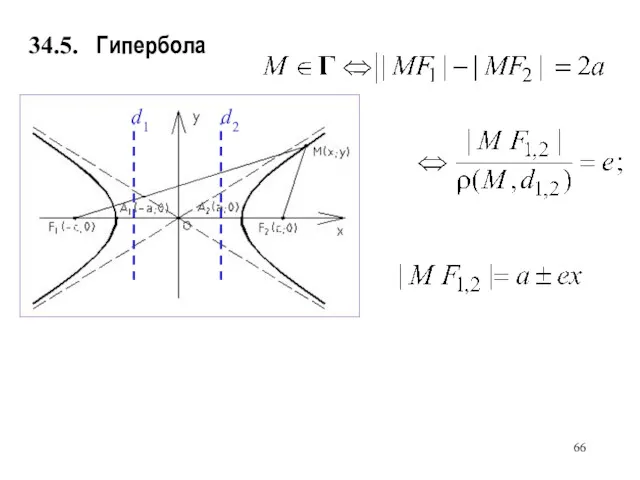
- 66. Гипербола d1 d2 34.5.
- 67. Гипербола Уравнение касательной в точке d1 d2 34.5.
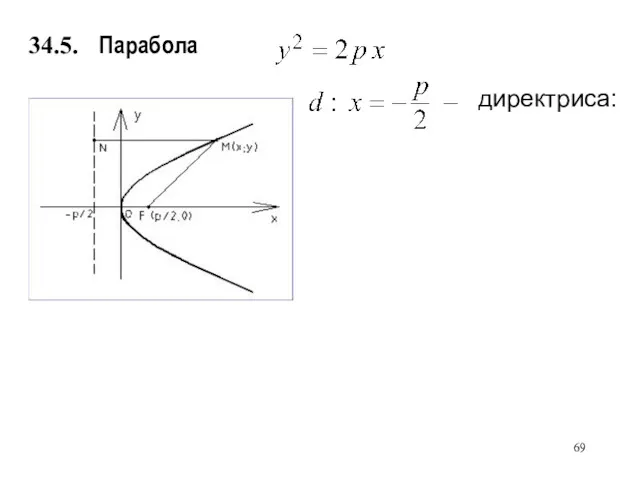
- 68. Парабола 34.5.
- 69. Парабола директриса: 34.5.
- 70. Парабола фокус; директриса: 34.5.
- 71. Парабола фокус; директриса: Уравнение касательной в точке 34.5.
- 72. уравнение кривой второго порядка имеет 34.6. в которой канонический вид, называется канонической. Система координат
- 73. Каноническая система координат определяется, вообще говоря, неоднозначно. уравнение кривой второго порядка имеет 34.6. в которой канонический
- 74. 35. Поверхности второго порядка
- 75. 35.1. Общее уравнение – п.д.с.к. 35. Поверхности второго порядка
- 76. 35.1. Общее уравнение – п.д.с.к. 35. Поверхности второго порядка Поверхностью второго порядка называется множество точек пространства,
- 77. 35.1. Общее уравнение Заменой переменных 35.2. – п.д.с.к. 35. Поверхности второго порядка (п. 33.6) (Q ‒
- 78. 35.1. Общее уравнение уравнение можно упростить, приведя квадратичную форму Заменой переменных 35.2. – п.д.с.к. 35. Поверхности
- 79. к главным осям, выбирая в пространстве новый базис Выбирая, если нужно, новое начало координат, 35.3. уравнение
- 80. к главным осям,
- 81. к главным осям, выбирая в пространстве новый базис
- 82. к главным осям, выбирая в пространстве новый базис Выбирая, если нужно, новое начало координат, 35.3.
- 83. к главным осям, выбирая в пространстве новый базис Выбирая, если нужно, новое начало координат, 35.3. уравнение
- 84. к главным осям, выбирая в пространстве новый базис Выбирая, если нужно, новое начало координат, 35.3. уравнение
- 85. Эллипсоиды: действительный (+) мнимый (−) ; 1) 2)
- 86. Эллипсоиды: действительный (+) мнимый (−) ; 1) 2) Гиперболоиды: 3) 4) однополостный (+) двуполостный (−);
- 87. Эллипсоиды: действительный (+) мнимый (−) ; 1) 2) Гиперболоиды: 3) 4) однополостный (+) двуполостный (−); Конусы:
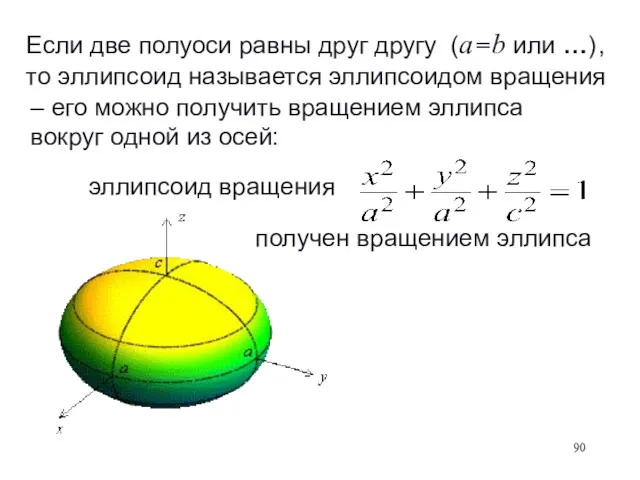
- 88. Если две полуоси равны друг другу (a = b или …) , то эллипсоид называется эллипсоидом
- 89. ‒ его можно получить вращением эллипса вокруг одной из осей: Если две полуоси равны друг другу
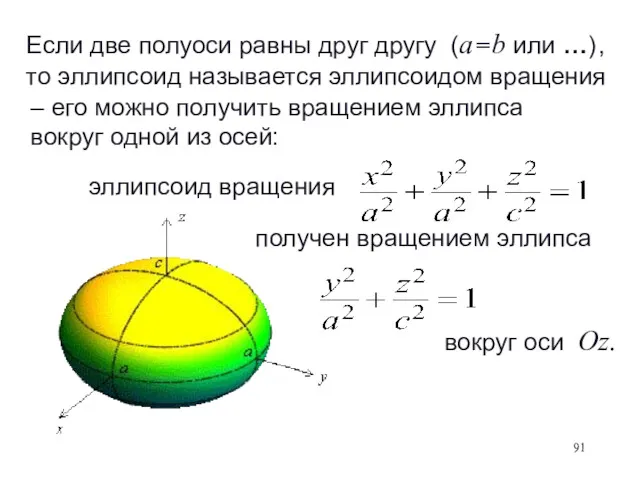
- 90. получен вращением эллипса эллипсоид вращения ‒ его можно получить вращением эллипса вокруг одной из осей: Если
- 91. получен вращением эллипса эллипсоид вращения вокруг оси Oz. ‒ его можно получить вращением эллипса вокруг одной
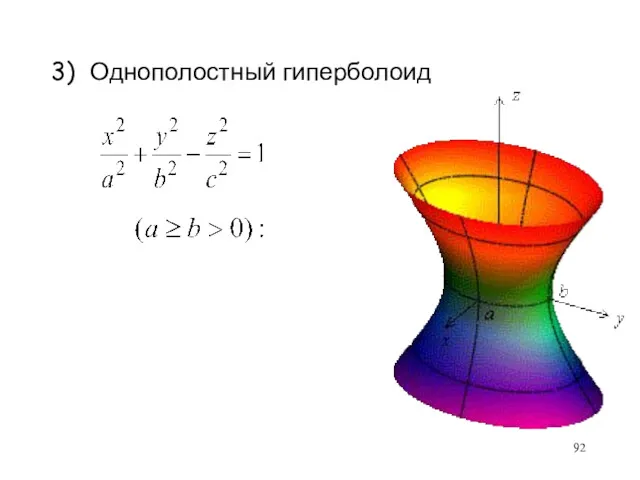
- 92. 3) Однополостный гиперболоид
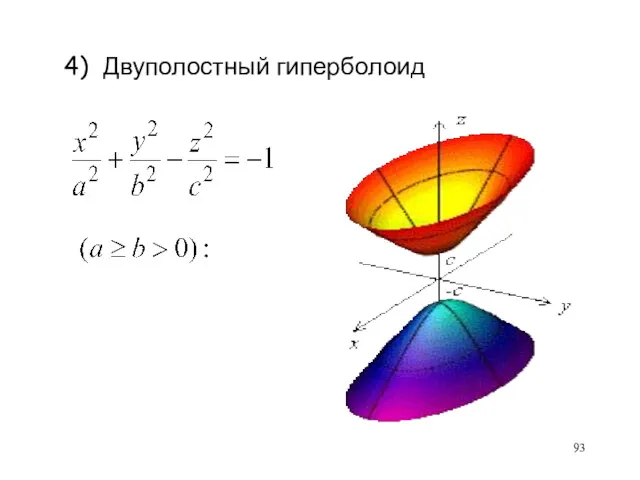
- 93. 4) Двуполостный гиперболоид
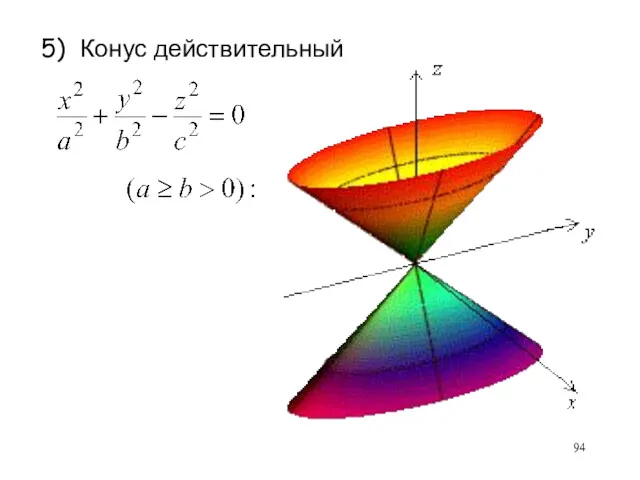
- 94. 5) Конус действительный
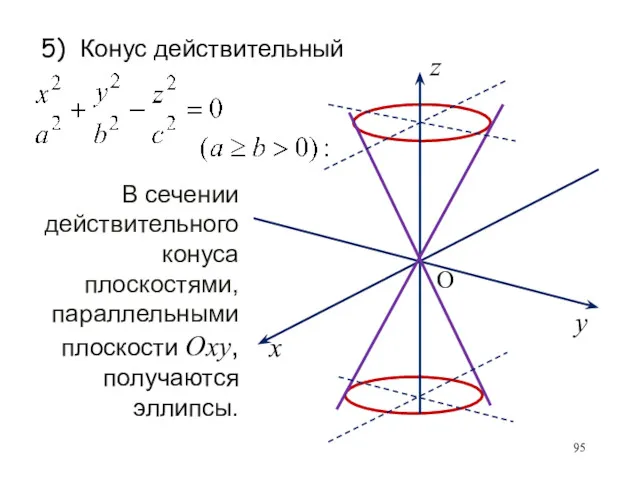
- 95. 5) Конус действительный O В сечении действительного конуса плоскостями, параллельными плоскости Охy, получаются эллипсы.
- 96. В сечении действительного конуса плоскостями, проходящими через ось Oz, получаются пары пересекающихся прямых. O
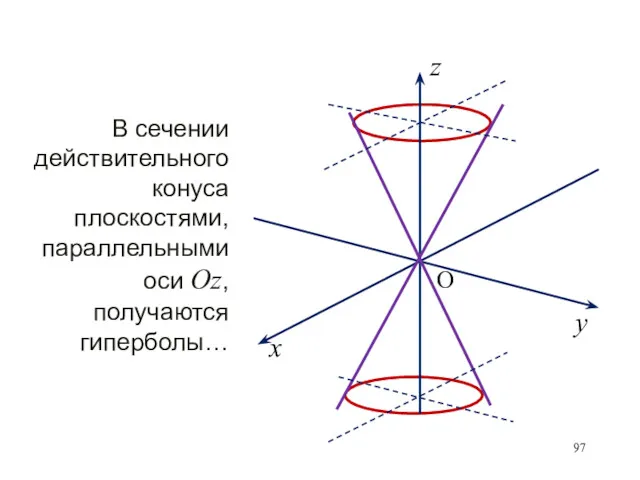
- 97. В сечении действительного конуса плоскостями, параллельными оси Oz, получаются гиперболы…
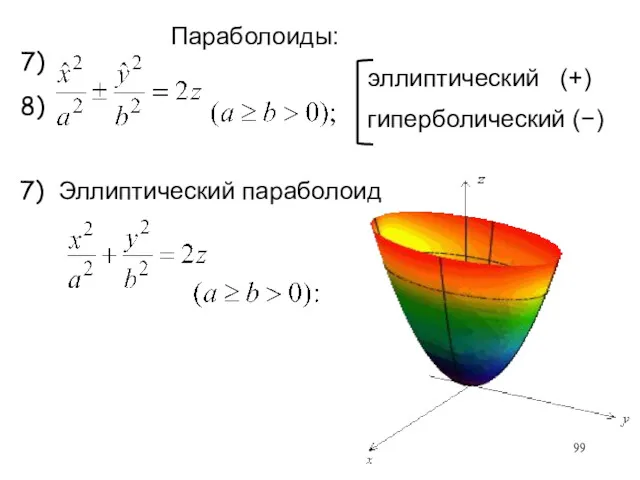
- 98. Параболоиды: эллиптический (+) гиперболический (−) 7) 8)
- 99. Параболоиды: эллиптический (+) гиперболический (−) 7) 8) 7) Эллиптический параболоид
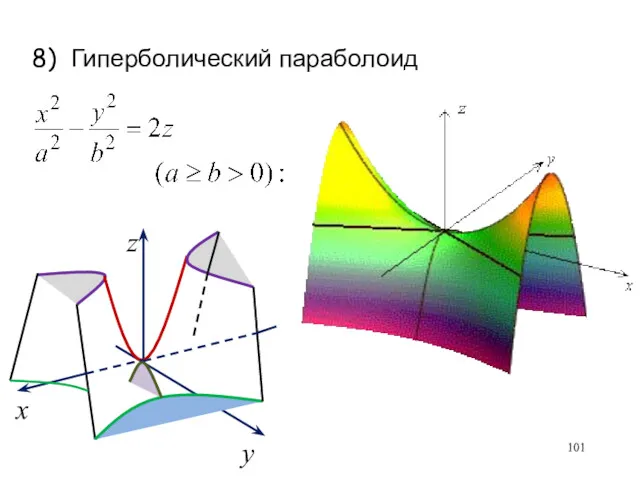
- 100. 8) Гиперболический параболоид
- 101. 8) Гиперболический параболоид
- 102. действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические
- 103. действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические 11) гиперболический:
- 104. действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические 14) − параболический; 11) гиперболический:
- 105. действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические 14) − параболический; пары плоскостей: 11) гиперболический:
- 106. пересекающихся действительных (−), мнимых (+); 12) 13) действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические 14)
- 107. пересекающихся действительных (−), мнимых (+); 12) 13) параллельных действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические
- 108. пересекающихся действительных (−), мнимых (+); 12) 13) параллельных действительный (−), мнимый (+) 9) 10) Цилиндры: эллиптические
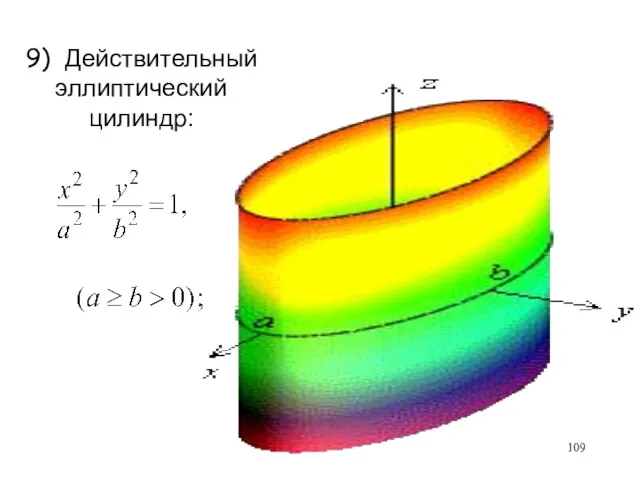
- 109. 9) Действительный эллиптический цилиндр:
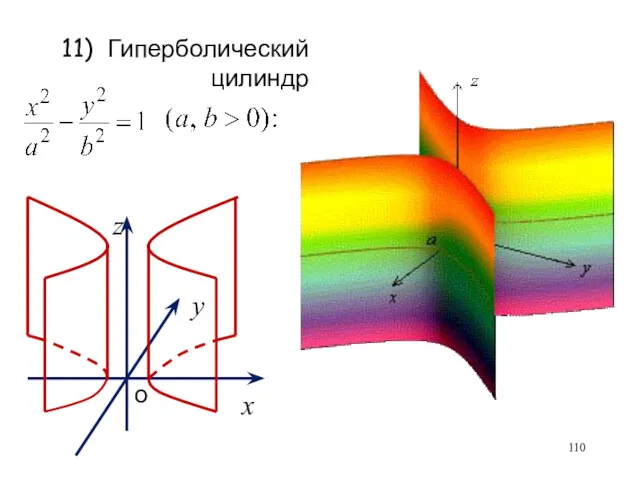
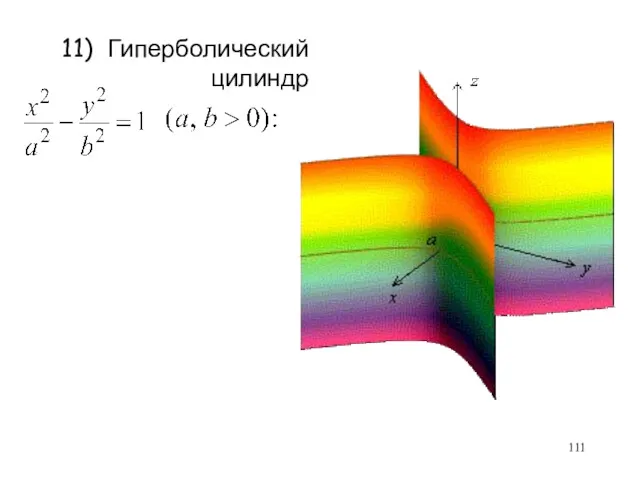
- 110. 11) Гиперболический цилиндр
- 111. 11) Гиперболический цилиндр
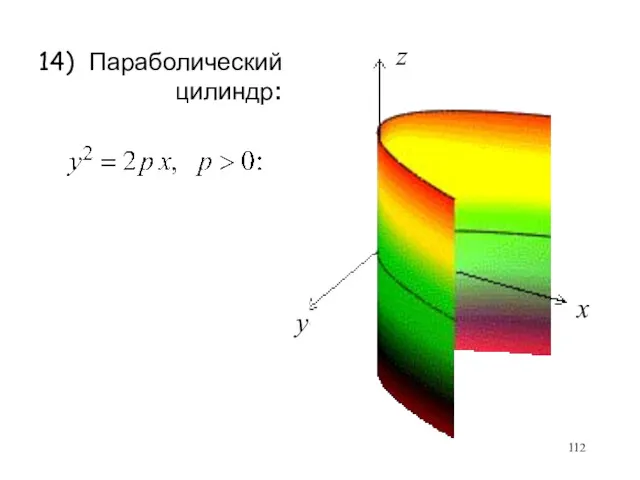
- 112. 14) Параболический цилиндр: x y z
- 113. Система координат в которой уравнение поверхности второго порядка имеет канонический вид, называется канонической. 35.4.
- 114. Система координат в которой уравнение поверхности второго порядка имеет канонический вид, называется канонической. 35.4. Каноническая система
- 115. 36.1. Общее уравнение и матрица Квадрикой в евклидовом пространстве называется 36. Квадрики в евклидовых пространствах множество
- 116. матрицу Уравнение квадрики можно переписать в матричном виде, а также в функциональной форме где ϕ и
- 117. пространстве можно привести к одному из трёх видов: 36.2. Уравнение всякой квадрики в евклидовом преобразованием неизвестных
- 118. Благодаря п. 33.6 можем считать, что квадратичная матрица перехода к ортонормированному базису форма приведена к главным
- 119. вид Выделяя полные квадраты, получаем уравнение и полагая и всё уравнение в новых неизвестных приобретает
- 121. Скачать презентацию
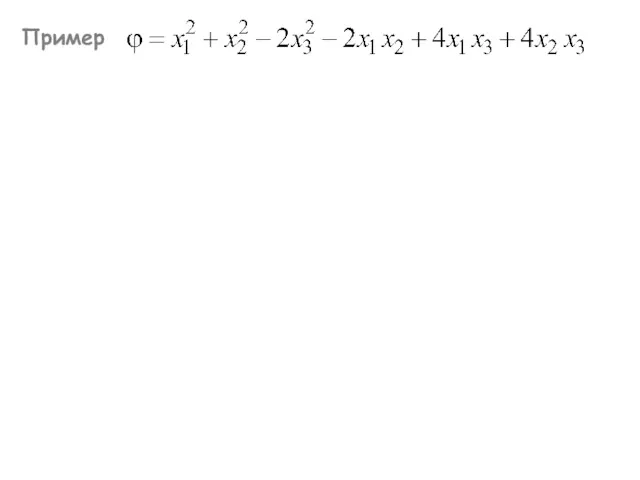
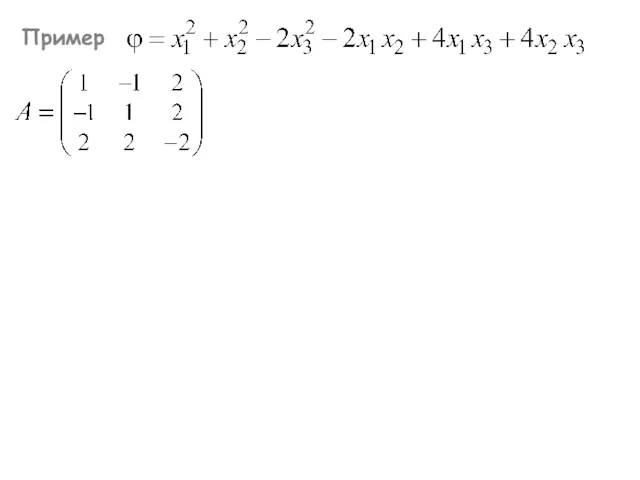




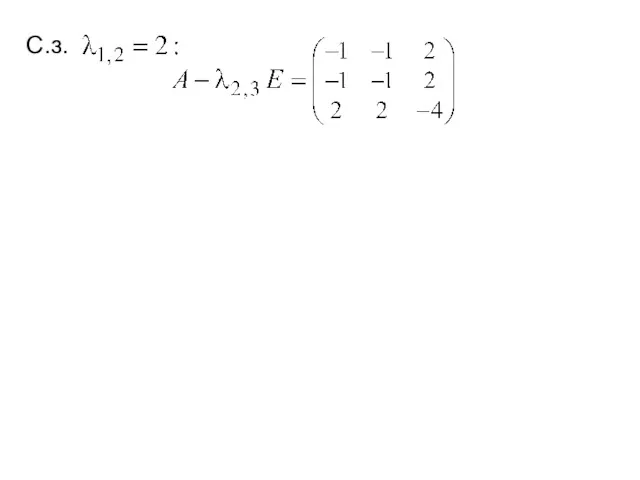
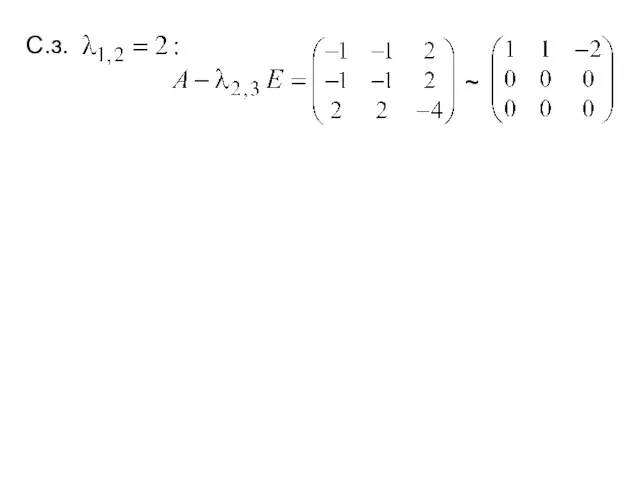
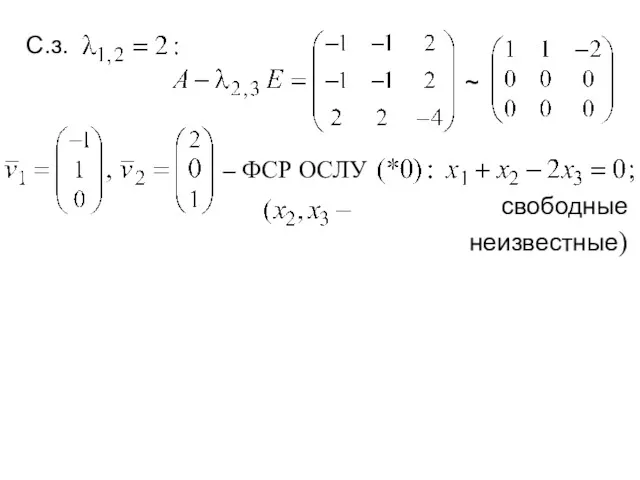







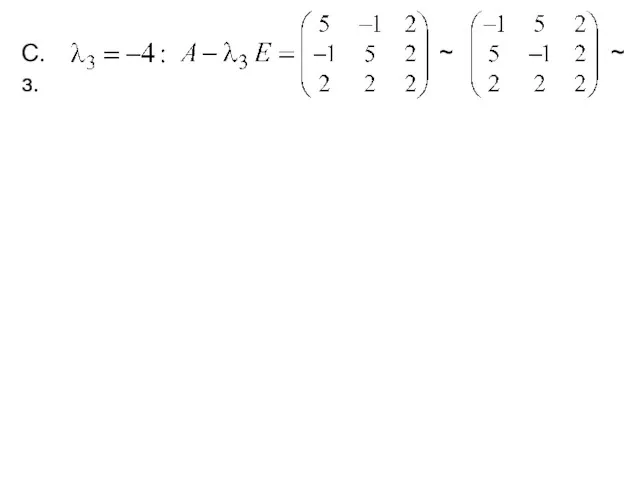
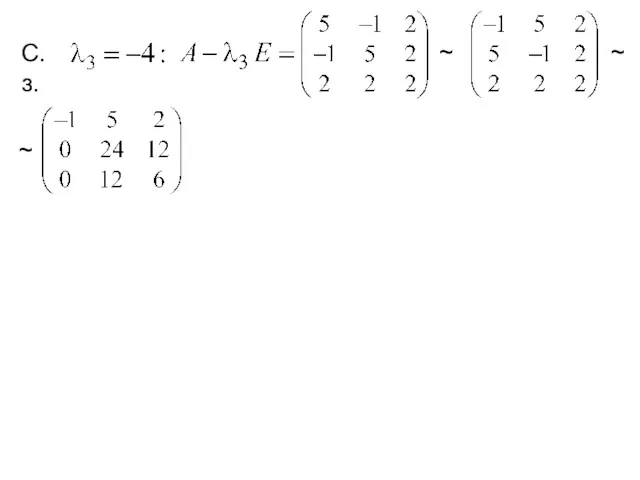
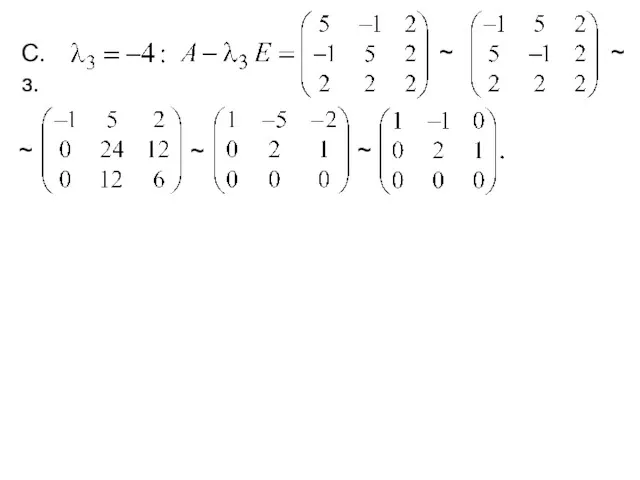










































































 Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла
Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла Корреляционный анализ данных. Лекция 9
Корреляционный анализ данных. Лекция 9 презентация по наглядной геометрии
презентация по наглядной геометрии Устный счет
Устный счет Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Диктанты на уроках геометрии в 8 классе
Диктанты на уроках геометрии в 8 классе Презентация к уроку математики 3 класс на тему Умножение трехзначного числа на однозначное
Презентация к уроку математики 3 класс на тему Умножение трехзначного числа на однозначное Предел функции
Предел функции Подобные треугольники. Пропорциональные отрезки
Подобные треугольники. Пропорциональные отрезки Свойства умножения натуральных чисел
Свойства умножения натуральных чисел Объем фигур
Объем фигур Кратчайшие пути из одной вершины в ориентированных ациклических графах. Алгоритм Дейкстры
Кратчайшие пути из одной вершины в ориентированных ациклических графах. Алгоритм Дейкстры Диференціальне числення. Похідна функції (лекція 1.2)
Диференціальне числення. Похідна функції (лекція 1.2) Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Математика в нашей жизни
Математика в нашей жизни Сетевые модели
Сетевые модели Неполные квадратные уравнения
Неполные квадратные уравнения Методики выполнения измерений, как основа метрологического обеспечения
Методики выполнения измерений, как основа метрологического обеспечения Математическая игра Поле чудес
Математическая игра Поле чудес Презентация Правильные и неправильные дроби
Презентация Правильные и неправильные дроби Формула корней квадратного уравнения
Формула корней квадратного уравнения компоненты сложения
компоненты сложения Сфера и шар
Сфера и шар Презентация к уроку математики Волшебные цифры Диск
Презентация к уроку математики Волшебные цифры Диск Методы проецирования. Проекции точки, проекции прямой (1 лекция)
Методы проецирования. Проекции точки, проекции прямой (1 лекция) Решение задач, с помощью квадратных уравнений
Решение задач, с помощью квадратных уравнений Из опыта работы Развитие математических представлений средствами фольклора и художественного слова
Из опыта работы Развитие математических представлений средствами фольклора и художественного слова Параллельность в пространстве. (Графическая работа 2)
Параллельность в пространстве. (Графическая работа 2)