Содержание
- 2. Понятие производной Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b),
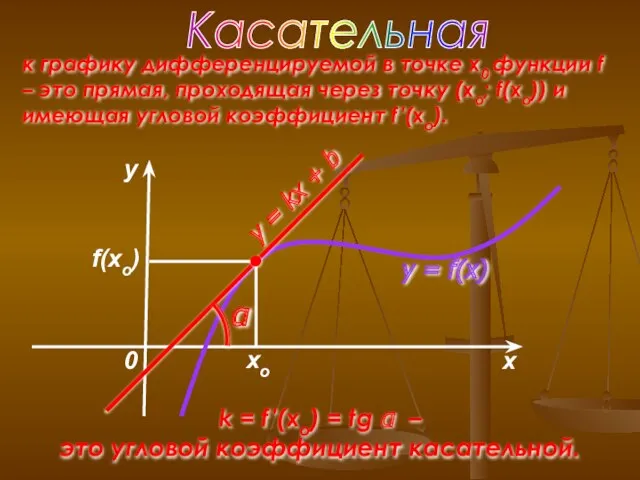
- 3. k = f ′(xo) = tg α – это угловой коэффициент касательной. f(xo) Касательная к графику
- 5. Приближенные вычисления f(x) ≈ f(xo) + f ′(xo)∆x (1) (2) (1 + ∆x)n ≈ 1 +
- 6. Общий вид уравнения касательной y = f ′(xo)(x – xo) + f(xo) Алгоритм составления уравнения касательной
- 7. Правила дифференцирования и таблица производных
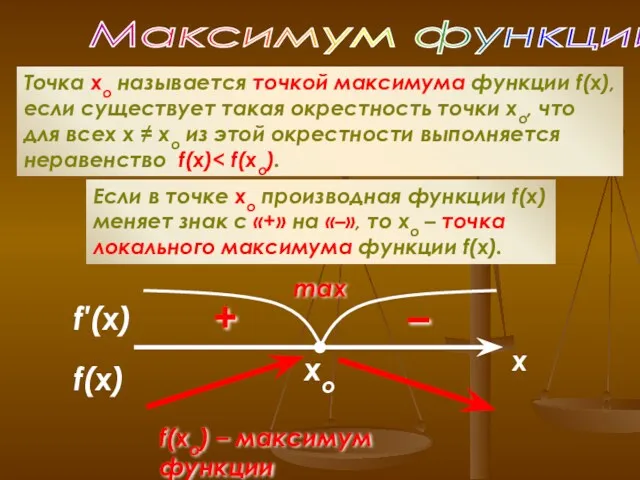
- 10. xo Максимум функции Точка хо называется точкой максимума функции f(x), если существует такая окрестность точки хо,
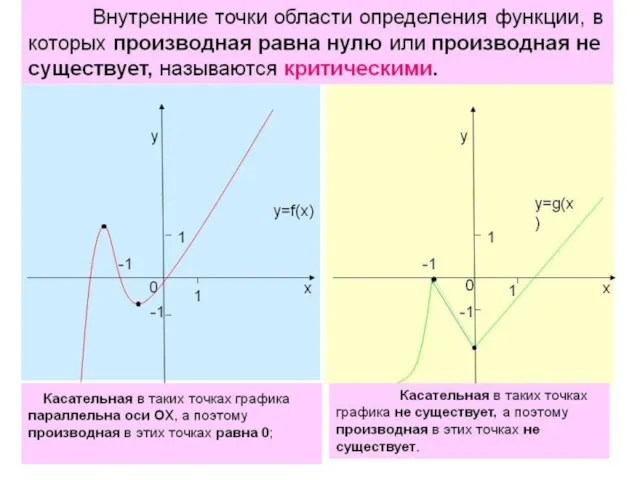
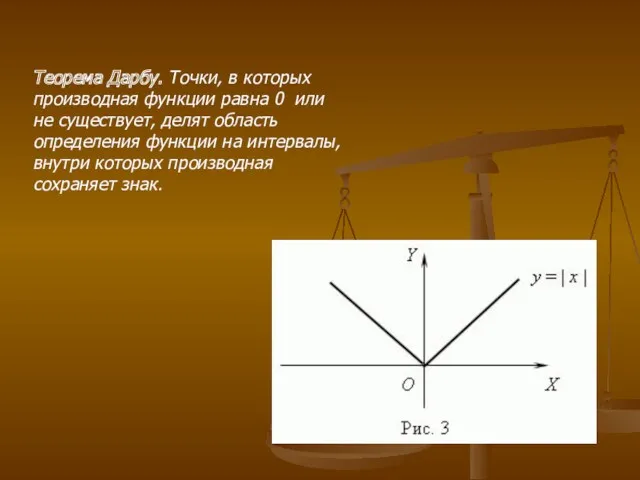
- 12. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции
- 13. Монотонность функций 1) Если f′(x) > 0 внутри промежутка I, то функция f возрастает на этом
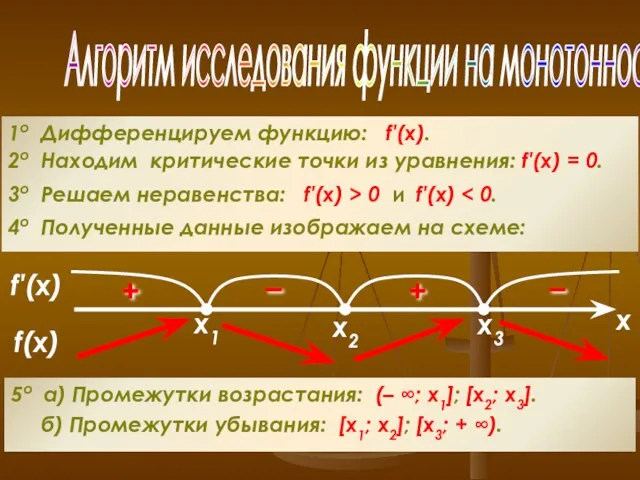
- 14. Алгоритм исследования функции на монотонность 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
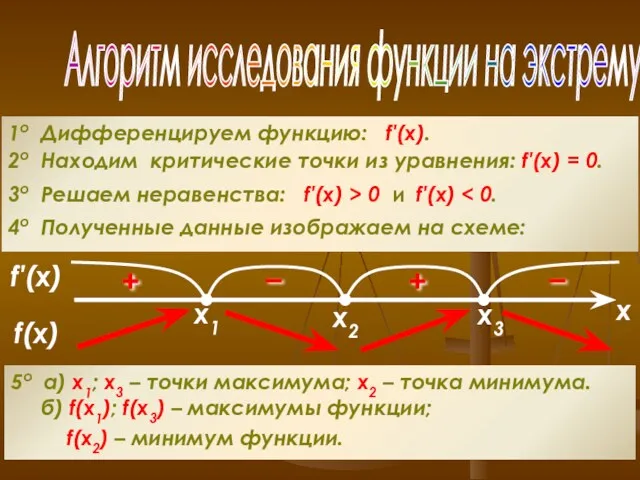
- 15. Алгоритм исследования функции на экстремумы 1о Дифференцируем функцию: f′(x). 2о Находим критические точки из уравнения: f′(x)
- 18. Скачать презентацию


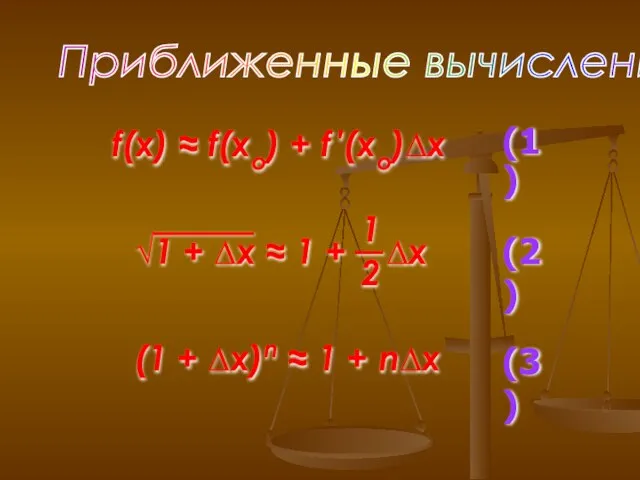






 Discrete Probability Distributions: Binomial and Poisson Distribution. Week 7 (2)
Discrete Probability Distributions: Binomial and Poisson Distribution. Week 7 (2) Многоугольник
Многоугольник Повторение курса алгебры
Повторение курса алгебры О чём расскажут старинные задачи?
О чём расскажут старинные задачи? Решение тригонометрических уравнений с отбором корней на заданном промежутке
Решение тригонометрических уравнений с отбором корней на заданном промежутке Геометрические тела
Геометрические тела Математика 2 кл. Презентация к уроку Меры длины УМК Перспектива
Математика 2 кл. Презентация к уроку Меры длины УМК Перспектива Увеличение и уменьшение числа в 10 и 100 раз
Увеличение и уменьшение числа в 10 и 100 раз Функция y=sinx и её график
Функция y=sinx и её график Прямоугольный параллелепипед
Прямоугольный параллелепипед Деление десятичных дробей на 10, 100,1000
Деление десятичных дробей на 10, 100,1000 Теория абстрактных автоматов
Теория абстрактных автоматов Быстрее, сильнее и правильнее. Пусть ум победит силу
Быстрее, сильнее и правильнее. Пусть ум победит силу Числовые промежутки
Числовые промежутки Графический диктант. Математика. 5 класс
Графический диктант. Математика. 5 класс Умножение чисел
Умножение чисел Расшифровка ребусов
Расшифровка ребусов Задачи на разностное сравнение. ! класс.
Задачи на разностное сравнение. ! класс. Числовые функции. Понятие функции
Числовые функции. Понятие функции Урок-игра Морской бой. 6 класс
Урок-игра Морской бой. 6 класс Урок математики в 1 классе Число и цифра семь
Урок математики в 1 классе Число и цифра семь Математика в филологии. Криптография и расшифровка древних текстов
Математика в филологии. Криптография и расшифровка древних текстов Частинні похідні вищих порядків. Змішані похідні. Теорема Шварца. Повний приріст і повний диференціал функції кількох змінних
Частинні похідні вищих порядків. Змішані похідні. Теорема Шварца. Повний приріст і повний диференціал функції кількох змінних Задачи на построение сечений
Задачи на построение сечений Презентация ТАНГРАМ Животные
Презентация ТАНГРАМ Животные Занимательный математический материал во всестороннем развитии дошкольников
Занимательный математический материал во всестороннем развитии дошкольников Многоугольники. Четырехугольники
Многоугольники. Четырехугольники Треугольник. Виды треугольников
Треугольник. Виды треугольников