Содержание
- 2. Mid-term exam 23/03/2017 11:45 – 13:00 hours Bring: Calculator Pen Eraser
- 3. Probability and cumulative probability distribution of a discrete random variable
- 4. The binomial distribution is used to find the probability of a specific or cumulative number of
- 5. Probability and cumulative probability distribution of a discrete random variable
- 6. Ch. 4- DR SUSANNE HANSEN SARAL Shape of Binomial Distribution The shape of the binomial distribution
- 7. Binomial Distribution shapes When P = .5 the shape of the distribution is perfectly symmetrical and
- 8. Using Binomial Tables instead of to calculating Binomial probabilities manually DR SUSANNE HANSEN SARAL Ch. 4-
- 9. Solving Problems with Binomial Tables MSA Electronics is experimenting with the manufacture of a new USB-stick
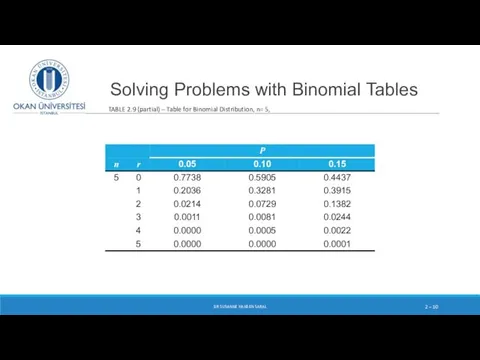
- 10. Solving Problems with Binomial Tables DR SUSANNE HANSEN SARAL 2 – TABLE 2.9 (partial) – Table
- 11. Solving Problems with Binomial Tables DR SUSANNE HANSEN SARAL 2 – n = 5, p =
- 12. Solving Problems with Binomial Tables Cumulative probability DR SUSANNE HANSEN SARAL 2 – TABLE 2.9 (partial)
- 13. Solving Problems with Binomial Tables Cumulative probabilities DR SUSANNE HANSEN SARAL 2 – TABLE 2.9 (partial)
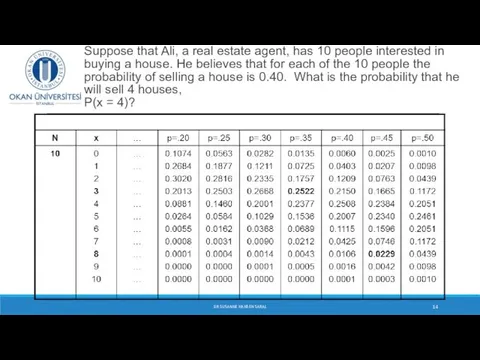
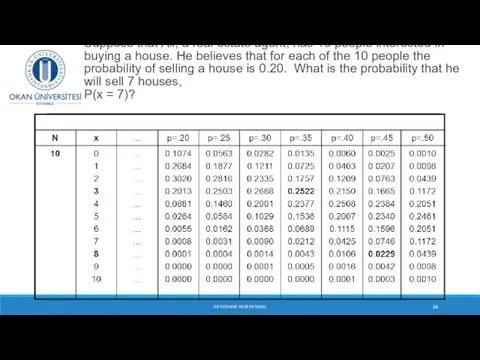
- 14. Suppose that Ali, a real estate agent, has 10 people interested in buying a house. He
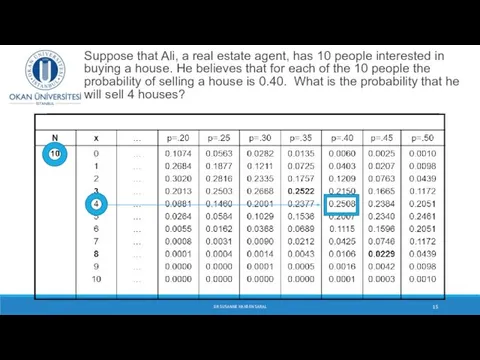
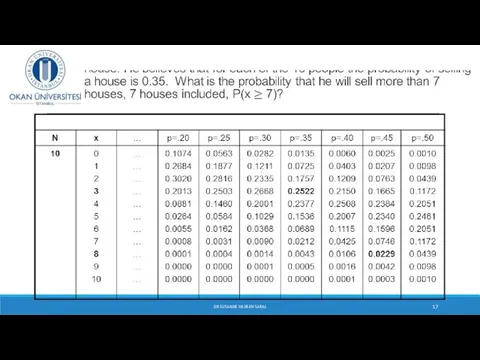
- 15. Suppose that Ali, a real estate agent, has 10 people interested in buying a house. He
- 16. Suppose that Ali, a real estate agent, has 10 people interested in buying a house. He
- 17. DR SUSANNE HANSEN SARAL
- 18. Probability Distributions Continuous Probability Distributions Binomial Probability Distributions Discrete Probability Distributions Uniform Normal Exponential DR SUSANNE
- 19. Poisson random variable, first proposed by Frenchman Simeon Poisson (1781-1840) DR SUSANNE HANSEN SARAL A Poisson
- 20. Poisson Random Variable - three requirements 1. The number of expected outcomes in one interval of
- 21. Poisson Random Variable - three requirements (continued) 2.The expected (or mean) number of outcomes over any
- 22. Examples of a Poisson Random variable The number of cars arriving at a toll booth in
- 23. Situations where the Poisson distribution is widely used: Capacity planning – time interval Areas of capacity
- 24. Poisson Probability Distribution Poisson Probability Function where: f(x) = probability of x occurrences in an interval
- 25. Example: Drive-up ATM Window Poisson Probability Function: Time Interval Suppose that we are interested in the
- 26. Poisson Probability Function: Time Interval λ = 10/15-minutes, x = 5 We want to know the
- 27. Using Poisson ProbabilityTables DR SUSANNE HANSEN SARAL Ch. 4- Example: Find P(X = 2) if λ
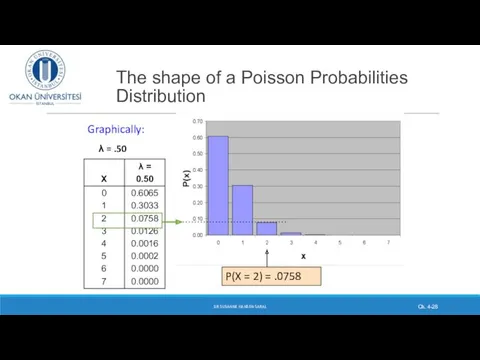
- 28. The shape of a Poisson Probabilities Distribution DR SUSANNE HANSEN SARAL Ch. 4- P(X = 2)
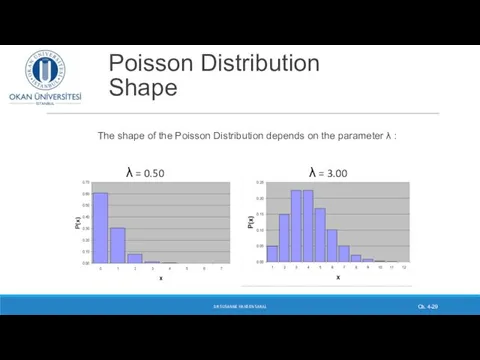
- 29. Poisson Distribution Shape The shape of the Poisson Distribution depends on the parameter λ : DR
- 30. Probability Distributions Continuous probability distributions Continuous Probability Distributions Binomial Probability Distributions Discrete Probability Distributions Uniform Normal
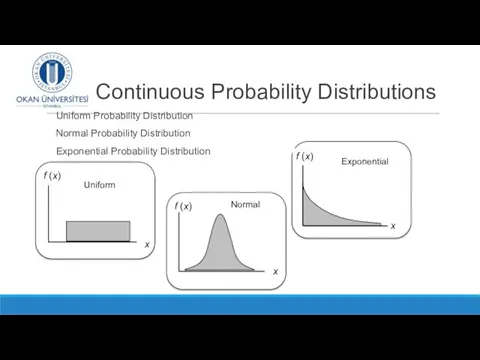
- 31. Continuous Probability Distributions Uniform Probability Distribution Normal Probability Distribution Exponential Probability Distribution f (x) x Uniform
- 32. Examples of continuous random variables include the following: The number of deciliters (dl) coca cola poured
- 33. Continuous random variable A continuous random variable can assume any value in an interval on the
- 34. f (x) x Uniform x f (x) Normal x f (x) Exponential Continuous Probability Distributions The
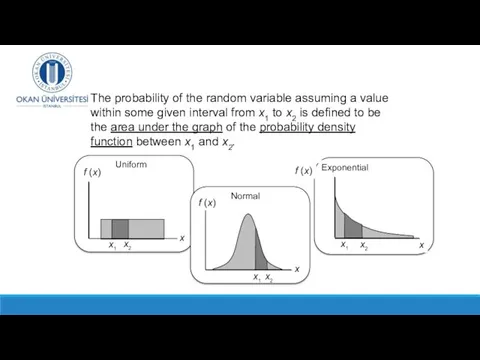
- 35. Probability Density Function The probability density function, f(x), of a continuous random variable X has the
- 36. Probability Density Function The probability density function, f(x), of random variable X has the following properties:
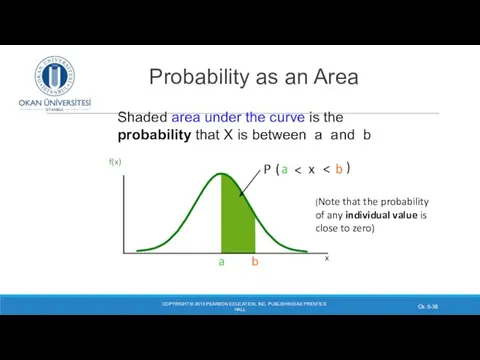
- 37. Probability as an Area COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch. 5-
- 38. Probability as an Area COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch. 5-
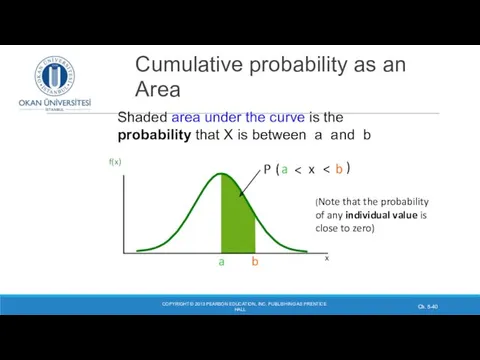
- 39. Cumulative Distribution Function, F(x) Let a and b be two possible values of X, with a
- 40. Cumulative probability as an Area COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch.
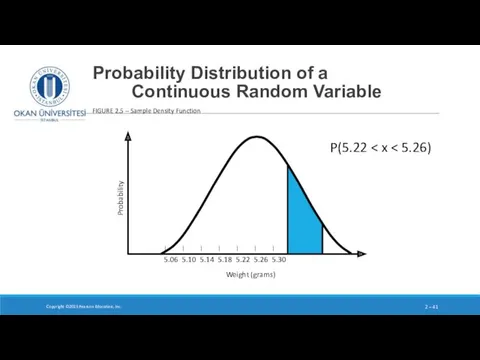
- 41. Probability Distribution of a Continuous Random Variable Copyright ©2015 Pearson Education, Inc. 2 – FIGURE 2.5
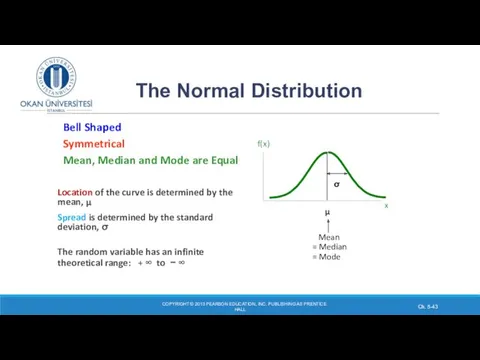
- 42. The Normal Distribution The Normal Distribution is one of the most popular and useful continuous probability
- 43. ‘Bell Shaped’ Symmetrical Mean, Median and Mode are Equal Location of the curve is determined by
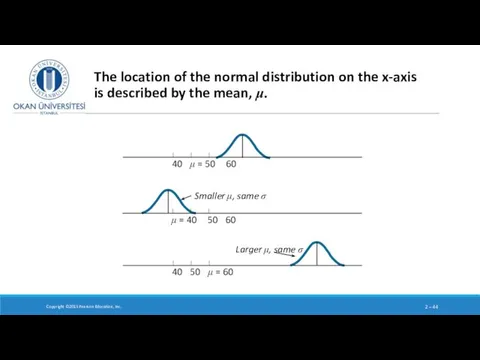
- 44. Copyright ©2015 Pearson Education, Inc. 2 – The location of the normal distribution on the x-axis
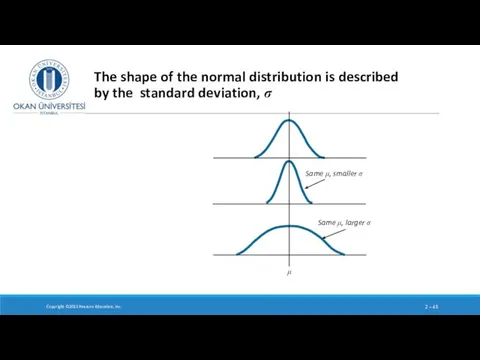
- 45. Copyright ©2015 Pearson Education, Inc. 2 – The shape of the normal distribution is described by
- 46. The Normal Distribution Copyright ©2015 Pearson Education, Inc. 2 –
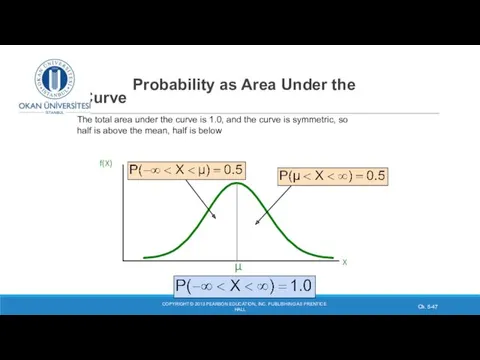
- 47. Probability as Area Under the Curve COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL
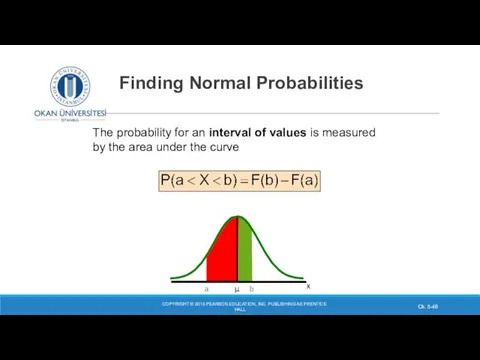
- 48. Finding Normal Probabilities COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch. 5- x
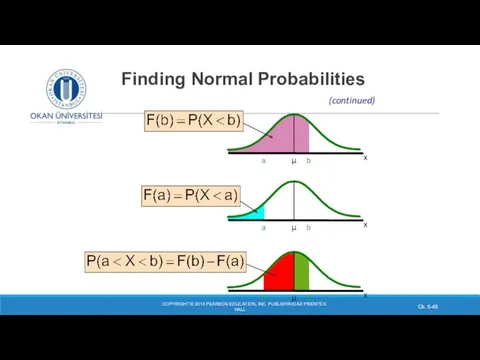
- 49. Finding Normal Probabilities COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch. 5- x
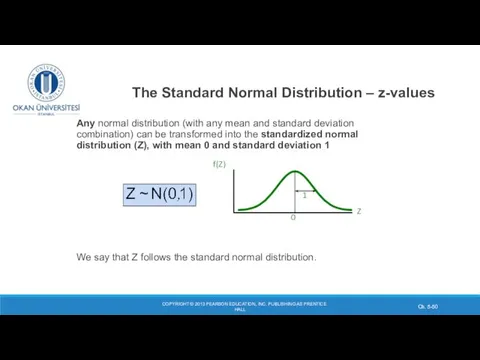
- 50. COPYRIGHT © 2013 PEARSON EDUCATION, INC. PUBLISHING AS PRENTICE HALL Ch. 5- The Standard Normal Distribution
- 51. Using the Standard Normal Table Step 1 Convert the normal distribution into a standard normal distribution
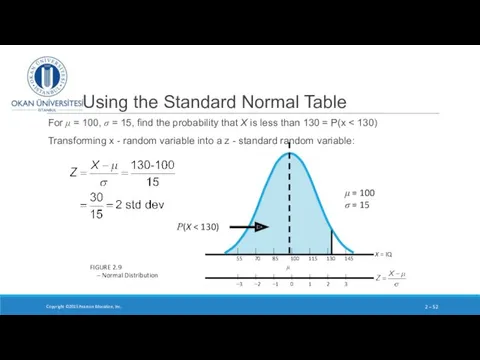
- 52. Using the Standard Normal Table For μ = 100, σ = 15, find the probability that
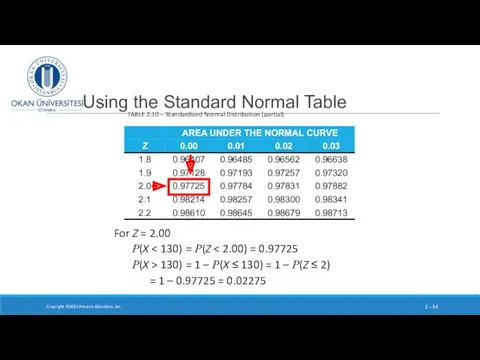
- 53. Using the Standard Normal Table Step 2 Look up the probability from the table of normal
- 54. Using the Standard Normal Table Copyright ©2015 Pearson Education, Inc. 2 – TABLE 2.10 – Standardized
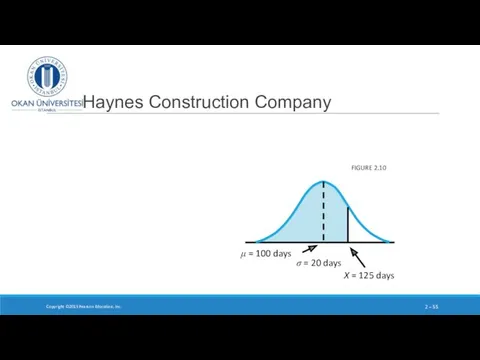
- 55. Haynes Construction Company Copyright ©2015 Pearson Education, Inc. 2 – FIGURE 2.10
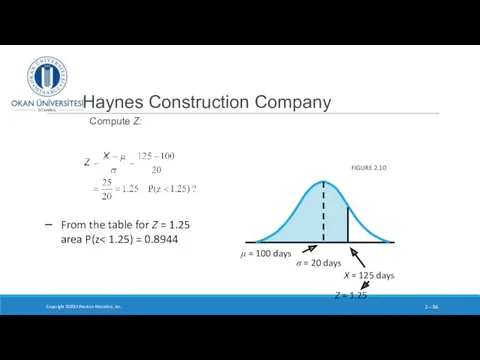
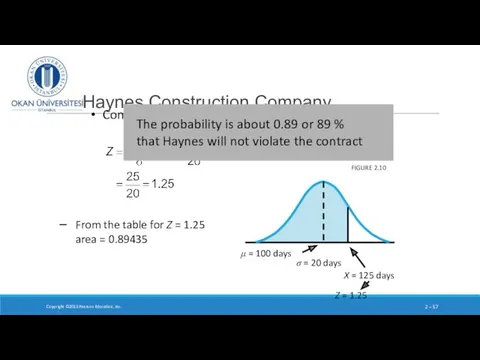
- 56. Haynes Construction Company Compute Z: Copyright ©2015 Pearson Education, Inc. 2 – FIGURE 2.10 From the
- 57. Compute Z Haynes Construction Company Copyright ©2015 Pearson Education, Inc. 2 – FIGURE 2.10 From the
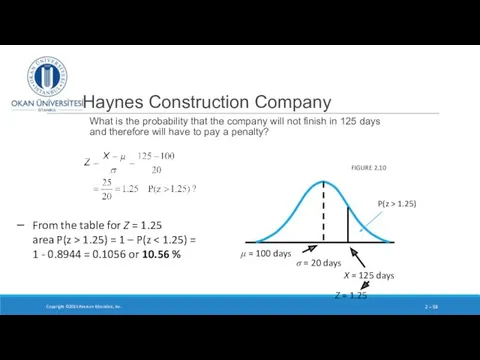
- 58. Haynes Construction Company What is the probability that the company will not finish in 125 days
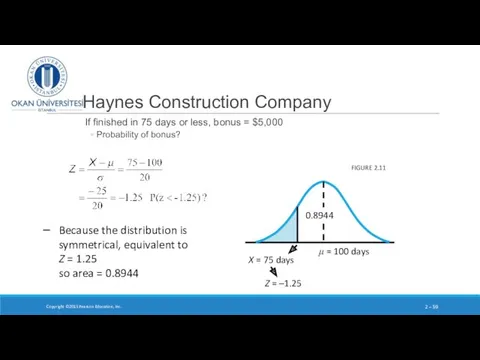
- 59. Haynes Construction Company If finished in 75 days or less, bonus = $5,000 Probability of bonus?
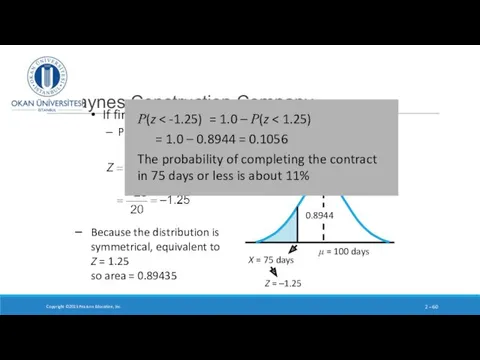
- 60. If finished in 75 days or less, bonus = $5,000 Probability of bonus? Haynes Construction Company
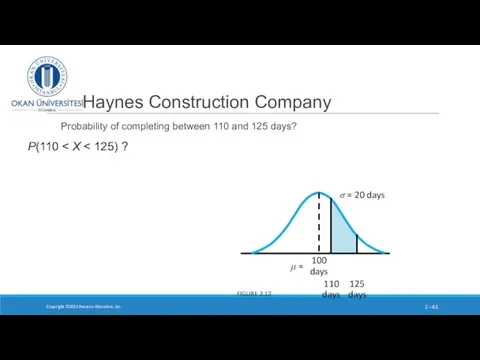
- 61. Haynes Construction Company Probability of completing between 110 and 125 days? Copyright ©2015 Pearson Education, Inc.
- 63. Скачать презентацию































 Методика обучения математике в начальной школе как педагогическая наука. Лекция 1
Методика обучения математике в начальной школе как педагогическая наука. Лекция 1 Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Решение задач с помощью систем уравнений
Решение задач с помощью систем уравнений Генеральная совокупность и частотное распределение. Измерение связи между качественными переменными
Генеральная совокупность и частотное распределение. Измерение связи между качественными переменными Измерение углов. Транспортир. 5 класс
Измерение углов. Транспортир. 5 класс Делимость чисел. Обобщение знаний
Делимость чисел. Обобщение знаний Математика. 1 класс. Урок 66. Решение задач - Презентация
Математика. 1 класс. Урок 66. Решение задач - Презентация Равнобедренный треугольник. Свойства равнобедренного треугольника. 7 класс
Равнобедренный треугольник. Свойства равнобедренного треугольника. 7 класс Множественный корреляционный анализ
Множественный корреляционный анализ Математические основы построения экспертной модели при расплывчатости границ между смежными рангами пожара
Математические основы построения экспертной модели при расплывчатости границ между смежными рангами пожара Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Конспект урока по математике 2 класс УМК Петерсон Л.Г. Свойства сложения + презентация
Конспект урока по математике 2 класс УМК Петерсон Л.Г. Свойства сложения + презентация Сложение и вычитание в пределах 10. Задачи в стихах.
Сложение и вычитание в пределах 10. Задачи в стихах. Закрепление навыков решения квадратных уравнений. Формирование у учащихся умения решать биквадратные уравнения. 8 класс
Закрепление навыков решения квадратных уравнений. Формирование у учащихся умения решать биквадратные уравнения. 8 класс Решение иррациональных уравнений
Решение иррациональных уравнений Решение примеров и задач на сложение и вычитание в пределах 20.
Решение примеров и задач на сложение и вычитание в пределах 20. Величины. Классная работа
Величины. Классная работа Призма, пирамида. Понятие и чертёж
Призма, пирамида. Понятие и чертёж Площадь фигур. Сравнение площадей
Площадь фигур. Сравнение площадей Критерии для принятия решений. Теория игр
Критерии для принятия решений. Теория игр Геометрические фигуры. Отрезок. Длина отрезка
Геометрические фигуры. Отрезок. Длина отрезка Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Уравнение окружности
Уравнение окружности Прикладная статистика. Меры центральной тенденции. Меры разброса. Нормальное распределение
Прикладная статистика. Меры центральной тенденции. Меры разброса. Нормальное распределение Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Архитектурная комбинаторика. Курс лекций
Архитектурная комбинаторика. Курс лекций Зачет по теме Квадратные уравнения
Зачет по теме Квадратные уравнения Длина окружности и площадь круга
Длина окружности и площадь круга