Слайд 2

Простые числа!
Простое число – не имеет делителей, кроме себя и 1,
и не равно 1:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, …
Слайд 3

Простые числа!
Простое число – не имеет делителей, кроме себя и 1,
и не равно 1:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, …
Основная теорема арифметики: каждое натуральное число единственным образом раскладывается в произведение простых.
Слайд 4

Слайд 5

Простых чисел бесконечно много
Евклид: предположим, что это не так, и что
всего есть n простых чисел p1, …, pn.
p1·…·pn + 1
Слайд 6

Простых чисел бесконечно много
Евклид: предположим, что это не так, и что
всего есть n простых чисел p1, …, pn.
p1·…·pn + 1
Нет делимости ни на одно из чисел p1, …, pn, т.к. в остатке получается 1.
Вывод: есть еще какие-то простые числа, кроме этих n. Противоречие.
Слайд 7

Промежутки между соседними простыми
1, 2, 2, 4, 2, 4, 2, 4,
6, 2, 6, 4, 2, 4, 6, 6, ...
Слайд 8
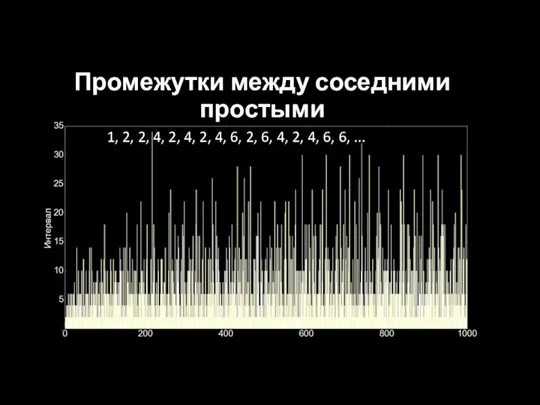
Промежутки между соседними простыми
1, 2, 2, 4, 2, 4, 2, 4,
6, 2, 6, 4, 2, 4, 6, 6, ...
Слайд 9

Проблема простых-близнецов
Простые-близнецы – пары простых чисел, отличающихся на 2:
3 и 5,
5 и 7, 11 и 13, …, 41 и 43, …, 1’000’000’007 и 1’000’000’009…
Бесконечно ли много таких пар?
Слайд 10

Проблема простых-близнецов
Простые-близнецы – пары простых чисел, отличающихся на 2:
3 и 5,
5 и 7, 11 и 13, …, 41 и 43, …, 1’000’000’007 и 1’000’000’009…
Бесконечно ли много таких пар?
Апрель 2013: пар, отличающихся не более чем на 70’000’000, бесконечно много.
Апрель 2014: пар, отличающихся не более чем на 246, бесконечно много.
Слайд 11

Проблема простых-близнецов
Простые-близнецы – пары простых чисел, отличающихся на 2:
3 и 5,
5 и 7, 11 и 13, …, 41 и 43, …, 1’000’000’007 и 1’000’000’009…
Бесконечно ли много таких пар? – нерешенная проблема.
Апрель 2013: пар, отличающихся не более чем на 70’000’000, бесконечно много.
Апрель 2014: пар, отличающихся не более чем на 246, бесконечно много.
Слайд 12

Насколько большими бывают промежутки?
Легкое упражнение: промежутки между соседними простыми могут быть
сколь угодно большими.
Слайд 13

Насколько большими бывают промежутки?
Легкое упражнение: промежутки между соседними простыми могут быть
сколь угодно большими.
Обозначение: n! = 1·2 ·3 ·… ·n.
100! + 2
100! + 3
100! + 4 99 подряд идущих непростых чисел.
…
100! + 100
Слайд 14

Насколько большими бывают промежутки?
Легкое упражнение: промежутки между соседними простыми могут быть
сколь угодно большими.
Обозначение: n! = 1·2 ·3 ·… ·n.
100! + 2
100! + 3
100! + 4 99 подряд идущих непростых чисел.
…
100! + 100
Вместо 100 можно было взять 1000000, 1000000000…
Слайд 15
![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-14.jpg)
Постулат Бертрана
На отрезке [n; 2n] всегда есть простое число.
Слайд 16
![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-15.jpg)
Постулат Бертрана
На отрезке [n; 2n] всегда есть простое число.
Первое доказательство: П.Л.Чебышёв,
1850 г.
Самое простое доказательство:
П. Эрдёш, 1932 г. (несколько страниц)
Слайд 17
![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-16.jpg)
Постулат Бертрана
На отрезке [n; 2n] всегда есть простое число.
Вопрос: Насколько малым
можно взять f (n), чтобы
на отрезке [n; n + n·f (n)] всегда было простое число?
Наилучший результат на сегодня: f (n) = n –19/40.
Слайд 18

Как часто встречаются простые числа?
Слайд 19
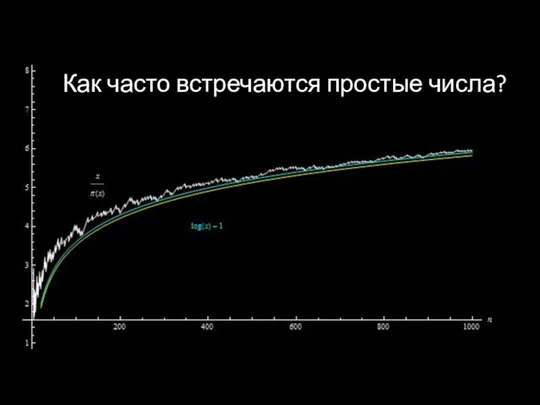
Как часто встречаются простые числа?
Слайд 20

Как часто встречаются простые числа?
ln x – натуральный логарифм: степень, в
которую нужно возвести число e, чтобы получить x
ln x = a ⇔ ea = x
e ≈ 2,718281828459045…
Слайд 21
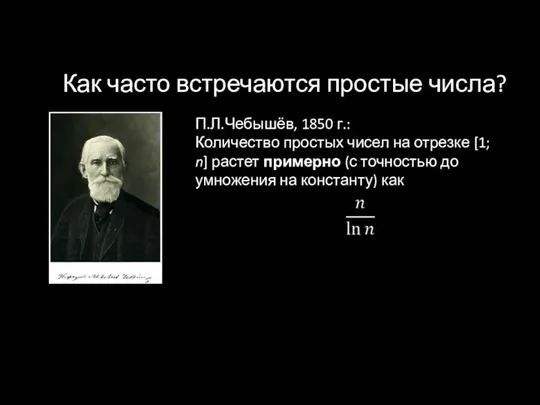
Как часто встречаются простые числа?
П.Л.Чебышёв, 1850 г.:
Количество простых чисел на отрезке
[1; n] растет примерно (с точностью до умножения на константу) как
Слайд 22

Как часто встречаются простые числа?
П.Л.Чебышёв, 1850 г.:
Количество простых чисел на отрезке
[1; n] растет примерно (с точностью до умножения на константу) как
Адамар, Валле-Пуссен, 1896 г.:
Константа равна 1.
Слайд 23

Как часто встречаются простые числа?
Пример: сколько простых чисел есть среди первых
10100 чисел?
Слайд 24

Слайд 25
Слайд 26














![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-14.jpg)
![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-15.jpg)
![Постулат Бертрана На отрезке [n; 2n] всегда есть простое число.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/236132/slide-16.jpg)









 Прибавление числа 3
Прибавление числа 3 Трикутники
Трикутники Возможности и использование системы компьютерной математики Scilab. Тема 3
Возможности и использование системы компьютерной математики Scilab. Тема 3 Действия с рациональными числами
Действия с рациональными числами Целые уравнения
Целые уравнения Умножение десятичных дробей на натуральное число
Умножение десятичных дробей на натуральное число Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Модуль числа. Классная работа
Модуль числа. Классная работа Презентация по математике 1 класс. Решение задач.
Презентация по математике 1 класс. Решение задач. Основы математической логики
Основы математической логики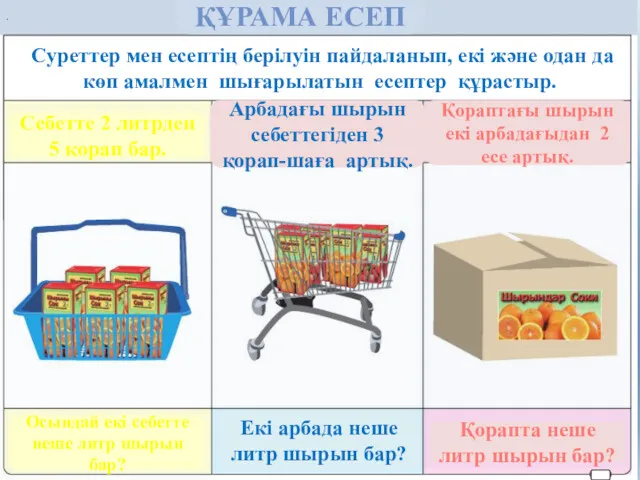 Құрама есеп
Құрама есеп Сумма углов треугольника
Сумма углов треугольника Ромб и квадрат
Ромб и квадрат Линейная модель парной регрессии. Лекция 4
Линейная модель парной регрессии. Лекция 4 Математический турнир. Презентация.
Математический турнир. Презентация. Повторення вивченого. Додаткові вправи. Урок №136
Повторення вивченого. Додаткові вправи. Урок №136 Теория графов. Дерево решений
Теория графов. Дерево решений Презентация к уроку Названия компонентов действий
Презентация к уроку Названия компонентов действий Игры с природой
Игры с природой Математико-статистическая обработка материалов научной и методической деятельности
Математико-статистическая обработка материалов научной и методической деятельности Состав числа 10
Состав числа 10 Свойства сложения. Формула и свойство
Свойства сложения. Формула и свойство Неопределенный интеграл. Основные понятия и определения
Неопределенный интеграл. Основные понятия и определения Аксиомы стереометрии
Аксиомы стереометрии Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости \арифметические действия. Сложение и вычитание. 4 класс
\арифметические действия. Сложение и вычитание. 4 класс Архимед. Іkaz.kz – ашық мәліметтер порталы
Архимед. Іkaz.kz – ашық мәліметтер порталы Умножение вектора на число
Умножение вектора на число