Содержание
- 2. Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников. Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.
- 3. Прямоугольный треугольник Прямоугольный треугольник
- 4. Треугольник называется прямоугольным, если у него есть прямой угол. ABC – прямоугольный ∠ C = 90°
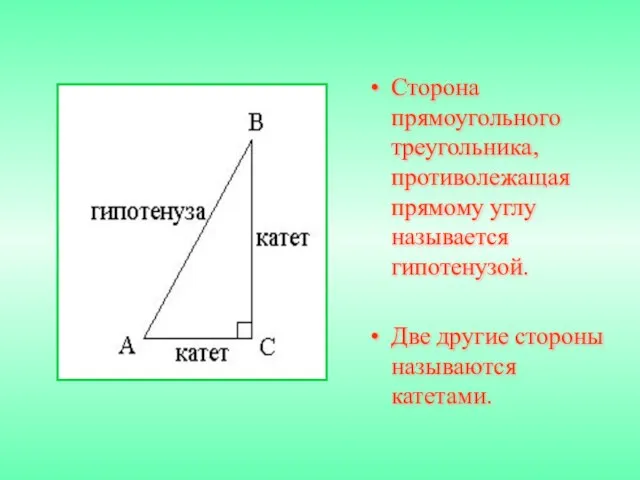
- 5. Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой. Две другие стороны называются катетами.
- 6. Признаки равенства прямоугольных треугольников Признаки равенства прямоугольных треугольников
- 7. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники
- 8. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного
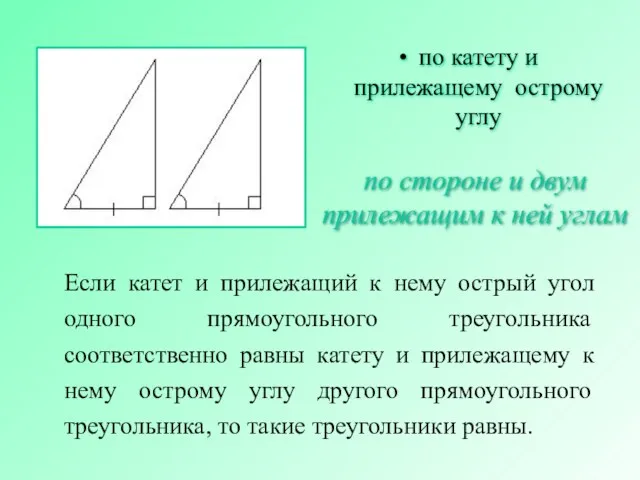
- 9. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему
- 10. Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу
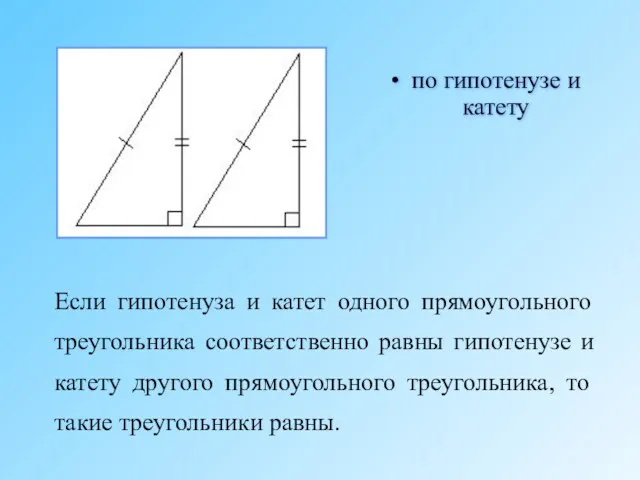
- 11. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то
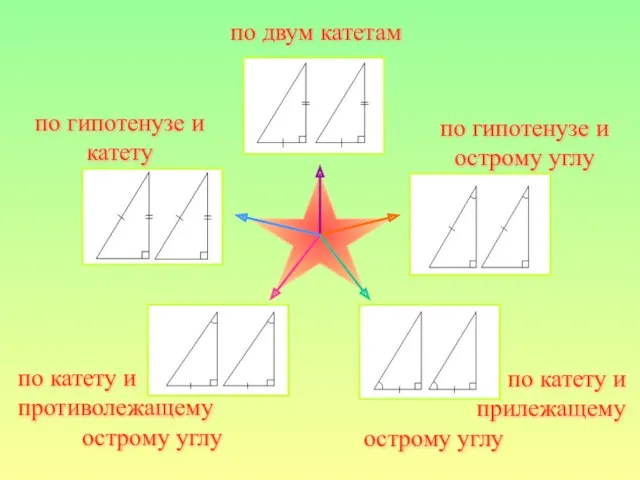
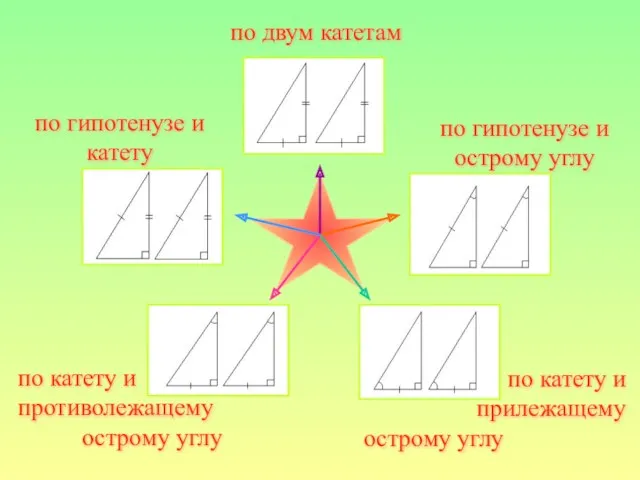
- 12. по двум катетам по гипотенузе и острому углу по катету и прилежащему острому углу по катету
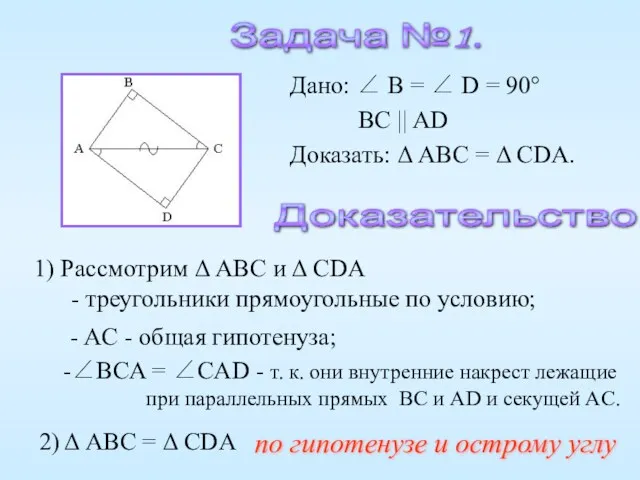
- 13. Задача №1. Доказательство. 1) Рассмотрим Δ ABC и Δ CDA - треугольники прямоугольные по условию;
- 14. Из точки D, лежащей на биссектрисе ∠ A, опущены перпендикуляры DB и DC на стороны угла.
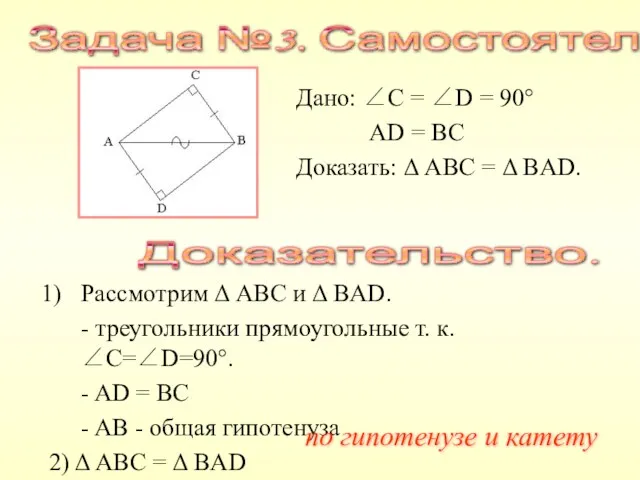
- 15. Дано: ∠C = ∠D = 90° AD = BC Доказать: Δ ABC = Δ BAD. Задача
- 16. Задача №4. Решение. 1) Рассмотрим ΔABO и ΔDCO. 2) ΔABO = ΔDCO по гипотенузе и острому
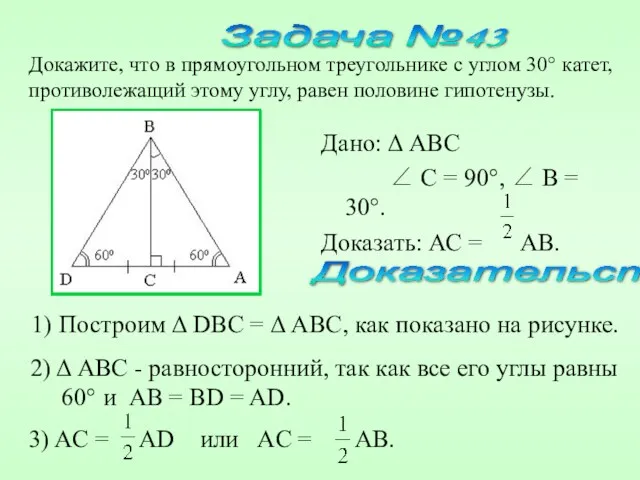
- 17. BC = AB Катет, лежащий против угла в 30°, равен половине гипотенузы. Свойство катета, лежащего против
- 18. Дано: Δ ABC ∠ C = 90°, ∠ B = 30°. Доказать: АС = АВ. Докажите,
- 19. Дано: Δ ABC - равнобедренный с основанием AC; ∠ B =120°; BD - медиана; BD =
- 20. Решение. Δ ABC – равнобедренный по условию. BD - медиана, биссектриса и высота. 3) Δ ABD
- 21. по двум катетам по гипотенузе и острому углу по катету и прилежащему острому углу по катету
- 23. Скачать презентацию












 Числовые выражения. 7 класс
Числовые выражения. 7 класс Формулы. Геометрия. (5 класс)
Формулы. Геометрия. (5 класс) мастер-класс для учителей начальной школы Магические квадраты
мастер-класс для учителей начальной школы Магические квадраты Формулы приведения
Формулы приведения Расположите однозначные ответы в порядке убывания. Доли. Обыкновенные дроби
Расположите однозначные ответы в порядке убывания. Доли. Обыкновенные дроби Перпендикулярность прямых и плоскостей. Повторение
Перпендикулярность прямых и плоскостей. Повторение Своя игра. Алгебра
Своя игра. Алгебра Действия с отрицательными и положительными числами на уроках математики и географии
Действия с отрицательными и положительными числами на уроках математики и географии Вектор. Определение. Длина (модуль) вектора
Вектор. Определение. Длина (модуль) вектора Множества и операции над множествами
Множества и операции над множествами Урок математики 3 класс Виды треугольников М.И. Моро
Урок математики 3 класс Виды треугольников М.И. Моро Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12)
Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12) Статистические ряды распределения и их виды
Статистические ряды распределения и их виды Презентация Как люди научились считать
Презентация Как люди научились считать Деление с остатком
Деление с остатком Симметрия относительно плоскости
Симметрия относительно плоскости Деление и дроби
Деление и дроби Осевая и центральная симметрия. Урок геометрии в 8 классе
Осевая и центральная симметрия. Урок геометрии в 8 классе Признаки делимости
Признаки делимости Раскрытие скобок. Математика. 6 класс
Раскрытие скобок. Математика. 6 класс Алгебраические дроби, сокращение дробей. 7 класс
Алгебраические дроби, сокращение дробей. 7 класс Прямая и обратная пропорциональные зависимости. (6 класс)
Прямая и обратная пропорциональные зависимости. (6 класс) Случаи сложения вида +7
Случаи сложения вида +7 Дециметр и метр
Дециметр и метр Решение уравнений и систем уравнений в рамках подготовки к ЕГЭ
Решение уравнений и систем уравнений в рамках подготовки к ЕГЭ Выбор рационального принципа структурного построения объектов наземной космической инфраструктуры. Лекция 21
Выбор рационального принципа структурного построения объектов наземной космической инфраструктуры. Лекция 21 Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Вычисление площадей фигур на клетчатой бумаге. Формула Пика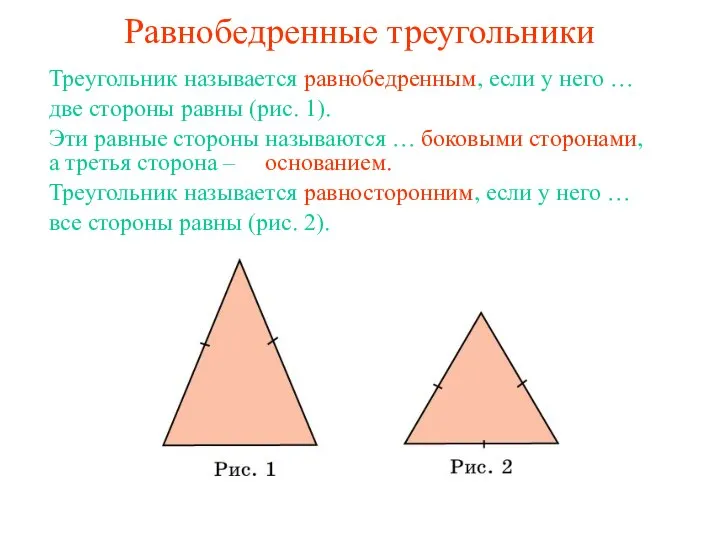 Равнобедренные треугольники
Равнобедренные треугольники