Содержание
- 2. Верите ли вы: - что число -5 - натуральное? - что натуральные числа использовали для счета
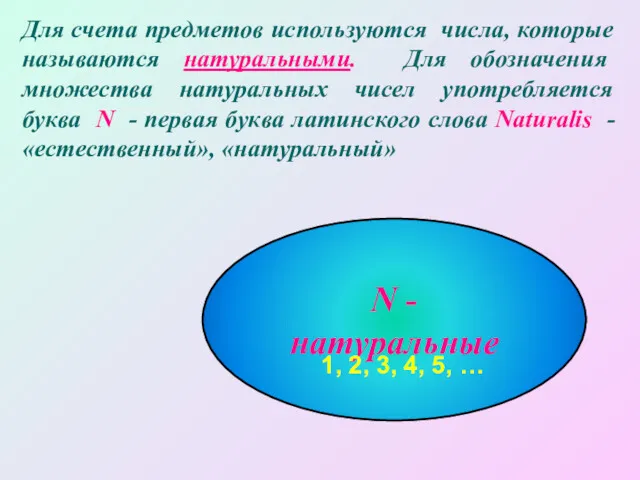
- 3. Для счета предметов используются числа, которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква N
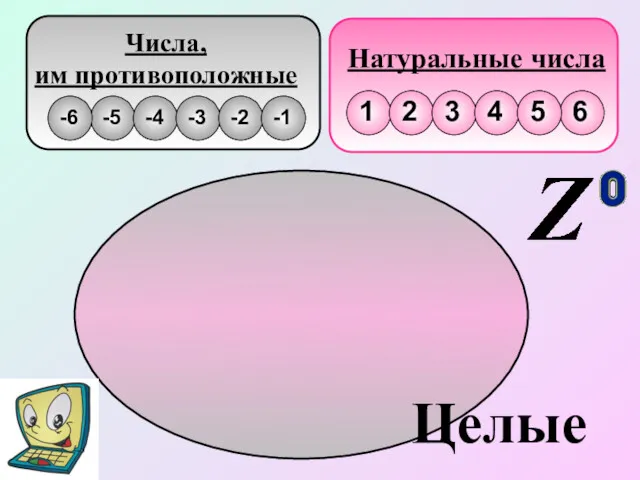
- 4. Натуральные числа Числа, им противоположные Целые
- 5. Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z -
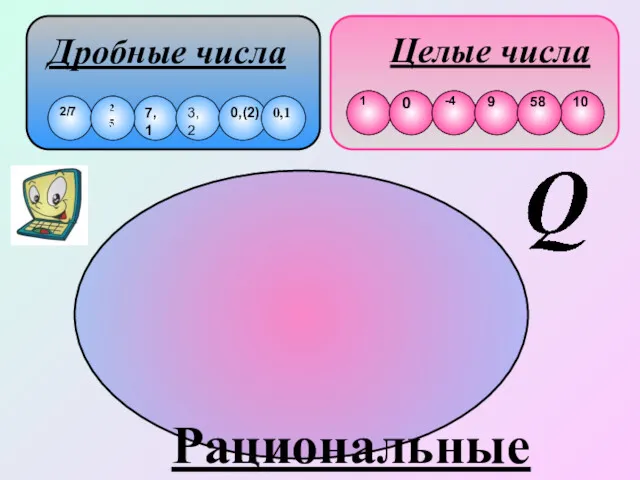
- 6. Целые числа Дробные числа Рациональные
- 7. Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q
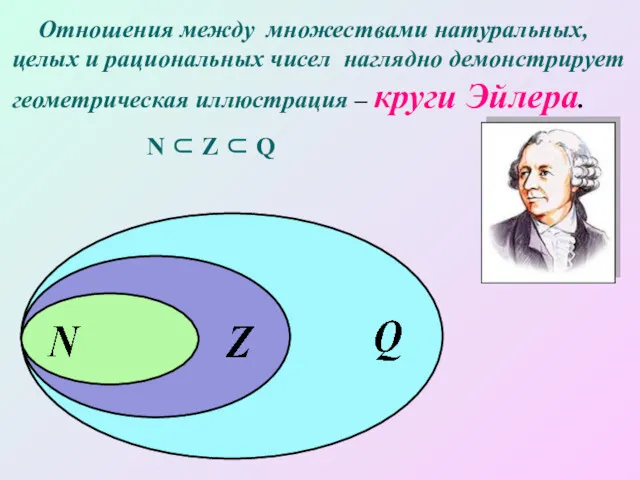
- 8. Отношения между множествами натуральных, целых и рациональных чисел наглядно демонстрирует геометрическая иллюстрация – круги Эйлера. N
- 9. Математический символ ∈ называют знаком принадлежности (элемент принадлежит множеству). «n - натуральное число» можно писать n
- 10. Математический символ ⊂ называют знаком включения (одно множество содержится в другом). «N - часть множества Z»
- 11. Множества обозначают большими буквами, элементы множества - маленькими буквами. «x не принадлежит множеству X» можно писать
- 12. N ⊂ Z ⊂ Q Число 5 - ? N, Z, Q Число -7 - ?
- 13. 1. нет 2. да 3. нет 4. да 5. да 6. нет 7. да 8. да
- 14. Критерии оценки: «5» - 15 «4» - 13-14 «3» - 10-12
- 15. Переведите обыкновенные дроби в десятичные: = 0,375 – конечная десятичная дробь Если в знаменателе стоят 2,
- 16. = 0,272727272727272727… - бесконечная периодическая десятичная дробь Для краткости написания – ПЕРИОД (круглые скобки) 0,272727272727272727…= 0,(27)
- 17. 0,(2) 2) 2,(21) 3) 1,(1) 4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
- 18. Рациональные числа Q Конечные десятичные дроби Бесконечные периодические десятичные дроби
- 19. Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби? N ⊂ Z ⊂ Q
- 20. Алгоритмы перевода рациональных чисел в бесконечную десятичную периодическую дробь = 0,375 = 0,375(0) = 0,272727… =
- 21. Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби? Наоборот, бесконечную периодическую десятичную дробь
- 22. Пусть х = 0,(2) 10х = 2,(2) х = 0,(2) 10х = 2,(2) 10х – х
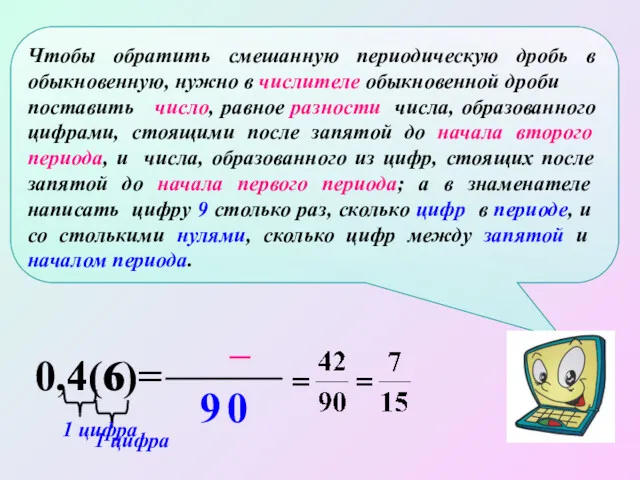
- 23. Пусть х = 0,4(6) 10х = 4,(6) 10х = 4,(6) 100х = 46,(6) 100х – 10х
- 24. Еще один интересный вариант перевода ...
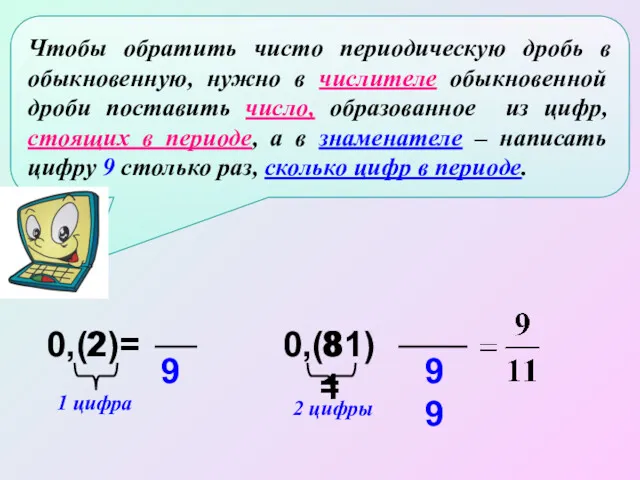
- 25. 0,(2)= 2 9 1 цифра 0,(81)= 81 2 цифры 99
- 26. Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, равное разности
- 27. на «3»: В А А4; Б3; В1; Г2 а) - 72 - 35,13 6 106,4
- 28. на «4»: 6. 0,(63) 7. Х = = = на «5»: 8. Х = = =
- 29. - Знаю (умею, научился), как определить вид числа, его принадлежность к числовым множествам; - Знаю (умею,
- 30. Домашнее задание: 1. Дана фраза: «28 - рациональное число». Как можно записать иначе? а) 28 ∈
- 32. Скачать презентацию






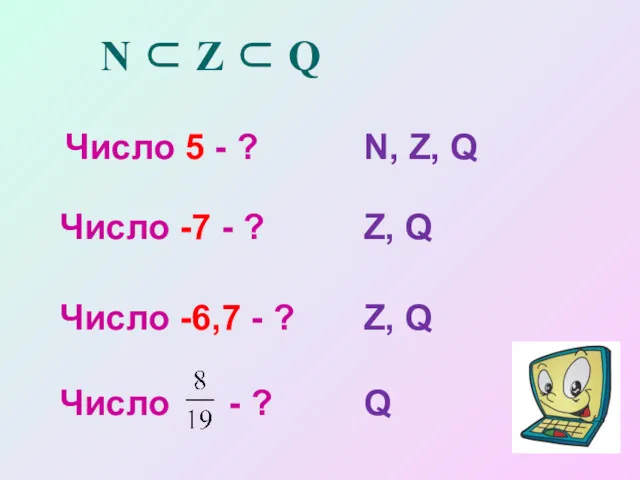













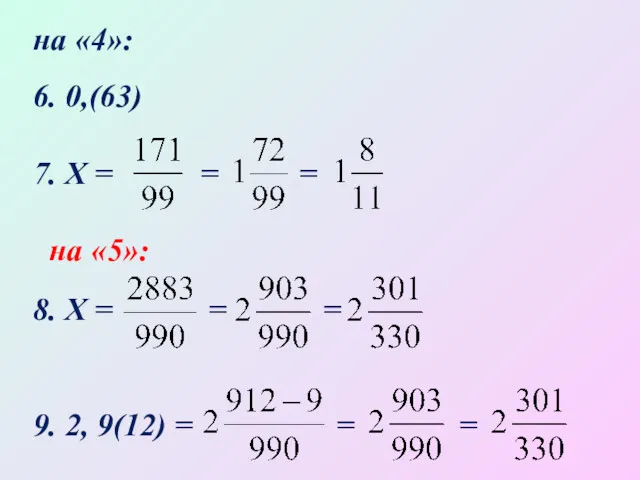


 Фигуры вращения
Фигуры вращения Движения
Движения Проект Камчатка в числах
Проект Камчатка в числах Развитие познавательных способностей через игры математической направленности Опыт работы воспитателя ГБДОУ №68 Калининского района Остроуховой Натальи Васильевны Диск
Развитие познавательных способностей через игры математической направленности Опыт работы воспитателя ГБДОУ №68 Калининского района Остроуховой Натальи Васильевны Диск Числовая последовательность
Числовая последовательность Презентация к уроку математики в 1 классе Решение простых задач
Презентация к уроку математики в 1 классе Решение простых задач Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100.
Методическая разработка урока математики во 2 классе на тему: Периметр. Программа Школа 2100. Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса
Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса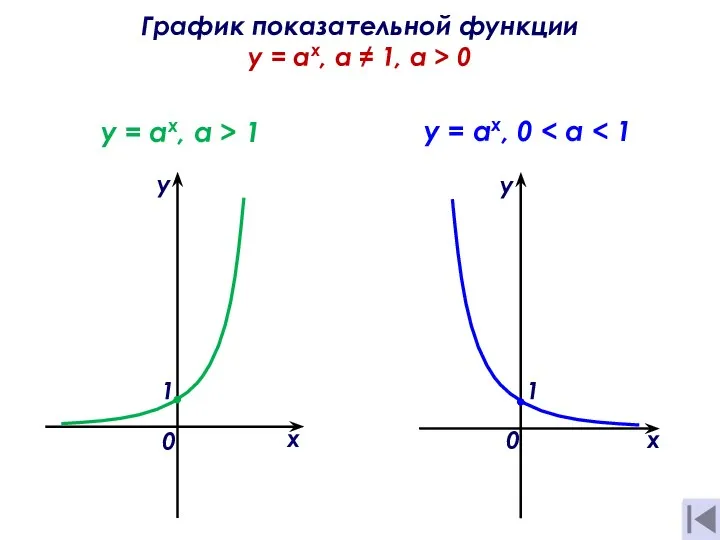 Показательные уравнения и неравенства с графиками
Показательные уравнения и неравенства с графиками Минимизация классических функций в классе ДНФ
Минимизация классических функций в классе ДНФ Квадратичная функция. Ее свойства и график
Квадратичная функция. Ее свойства и график Дискриминантный анализ
Дискриминантный анализ Множества. Элементы множества
Множества. Элементы множества Использование подобия треугольников при решении задач практического содержания
Использование подобия треугольников при решении задач практического содержания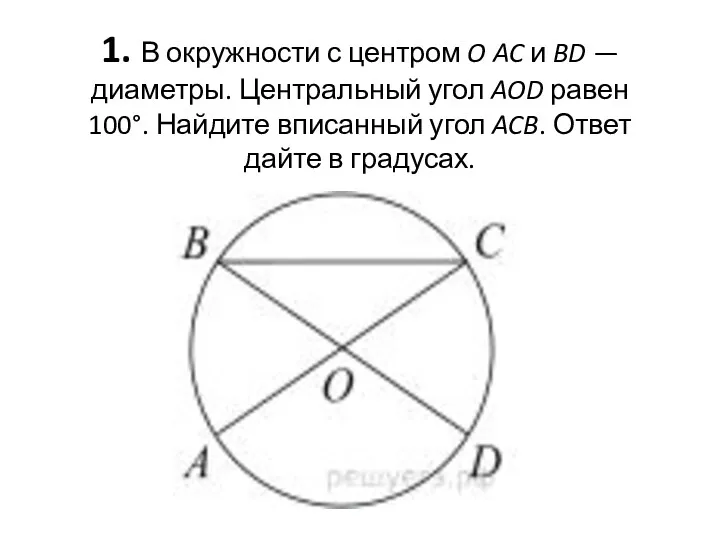 Окружности с центром O
Окружности с центром O Множества и операции над ними. Решение задач с помощью кругов Эйлера
Множества и операции над ними. Решение задач с помощью кругов Эйлера Свойства прямоугольного треугольника. Геометрия 7 класс
Свойства прямоугольного треугольника. Геометрия 7 класс Верно/неверно. Математические примеры
Верно/неверно. Математические примеры в гости к звездочету
в гости к звездочету Решение задач №19. Проценты
Решение задач №19. Проценты Воображаемая геометрия Н.И. Лобачевского
Воображаемая геометрия Н.И. Лобачевского Измерение углов
Измерение углов Литературная математика
Литературная математика Вписанная окружность. 8 класс
Вписанная окружность. 8 класс Критерий согласия. Практический пример применения критерия согласия. Закон Менделя
Критерий согласия. Практический пример применения критерия согласия. Закон Менделя Система подготовки к ЕГЭ
Система подготовки к ЕГЭ Математические модели
Математические модели Площадь (тест для учащихся 3-4 классов)
Площадь (тест для учащихся 3-4 классов)