Содержание
- 2. Дифференциальные уравнения устанавливают связь между независимыми переменными, искомыми функциями и их производными. Если искомая функция зависит
- 3. Постановка задачи Например, условие равновесия упругой среды описывается обыкновенным дифференциальным уравнением: Здесь искомая функция (механическое напряжени)
- 4. Постановка задачи В том случае, если искомая функция зависит от нескольких переменных, дифференциальное уравнение будет уравнением
- 5. Постановка задачи Обыкновенными дифференциальными уравнениями (ОДУ) называются уравнения, которые содержат одну или несколько производных от искомой
- 6. Постановка задачи Из общей записи дифференциального уравнения можно выразить производную в явном виде: Уравнение для производных
- 7. Постановка задачи В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование
- 8. Постановка задачи Второй тип задач – это, так называемые, граничные, или краевые, в которых дополнительные условия
- 9. Постановка задачи Сформулируем задачу Коши. Найти решение обыкновенного дифференциального уравнение (ОДУ) первого порядка, разрешенное относительно производной
- 10. Постановка задачи Необходимо найти на отрезке [x0,xn] такую непрерывную функцию y = y(x), которая удовлетворяет дифференциальному
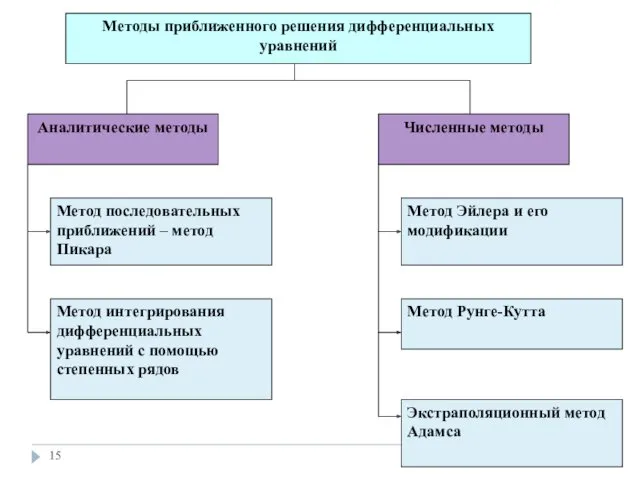
- 11. * y’=x2 xdy=y3dx Обыкновенные дифференциальные уравнений Уравнения в частных производных
- 12. * y′=x2 xdy=y3dx Уравнения первого порядка Уравнения второго порядка
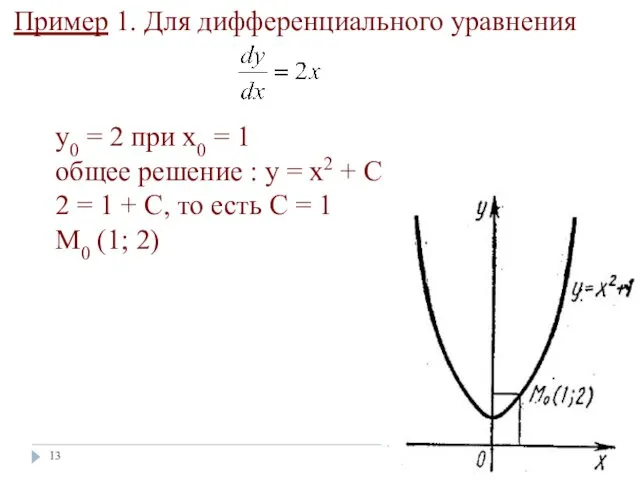
- 13. * Пример 1. Для дифференциального уравнения y0 = 2 при х0 = 1 общее решение :
- 14. * Условие Липшица
- 15. *
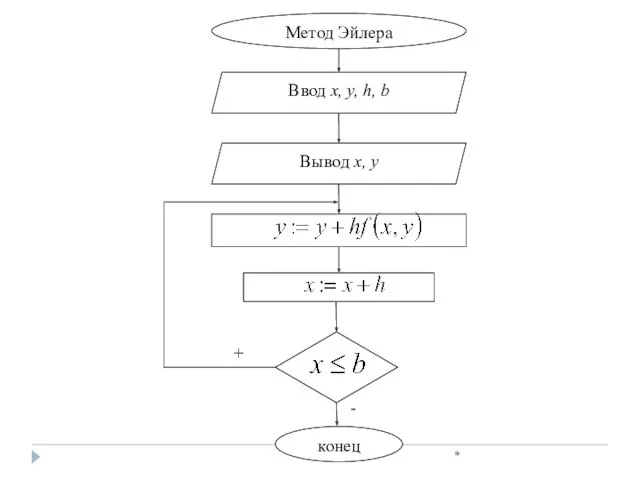
- 16. * Метод Эйлера
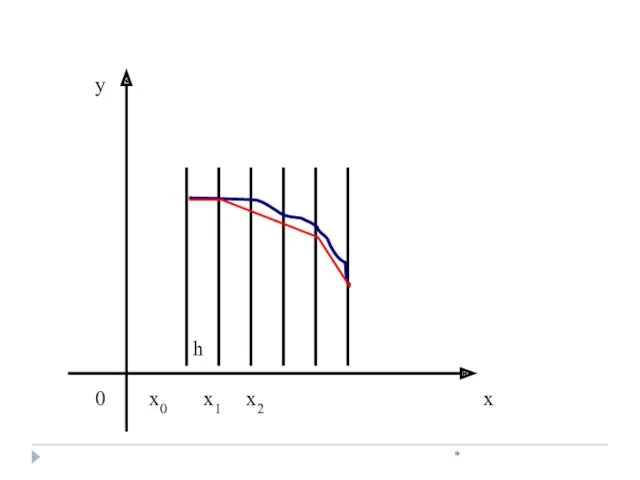
- 17. * Решить дифференциальное уравнение у′=f(x, y) численным методом – это значит для заданной последовательности аргументов х0,
- 18. * Пусть дано дифференциальное уравнение первого порядка y’= f (x, y) с начальным условием x=x0, y(x0)=y0
- 19. *
- 20. * то есть
- 21. * Обозначим
- 22. *
- 23. * Погрешность метода где
- 24. * Пример 1. Решить у’=у-x с начальным условием х0=0, у0=1.5 на отрезке [0;1.5], h=0.25 Решение
- 25. *
- 26. * Усовершенствованный метод Эйлера yn+1 = yn + h·[f(tn, yn) + f(tn+1 , y*n+1 )]/2 вернемся
- 27. * МЕТОД РУНГЕ-КУТТЫ
- 28. * Задача. Пусть дано дифференциальное уравнение первого порядка y’= f(x, y) с начальным условием x=x0, y(x0)=y0
- 29. *
- 30. *
- 31. *
- 32. * Погрешность метода Rn(h5)
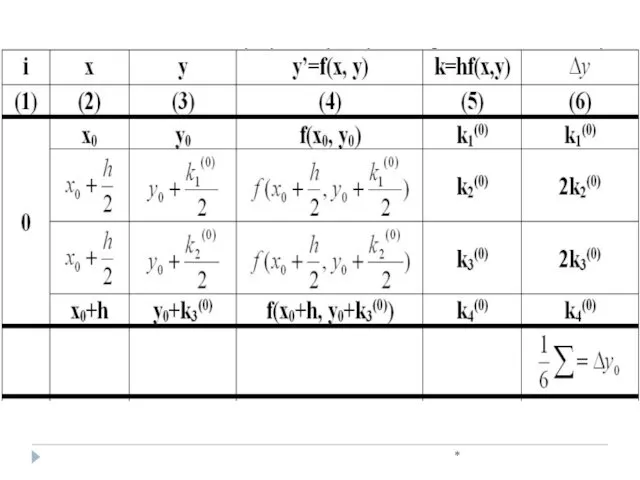
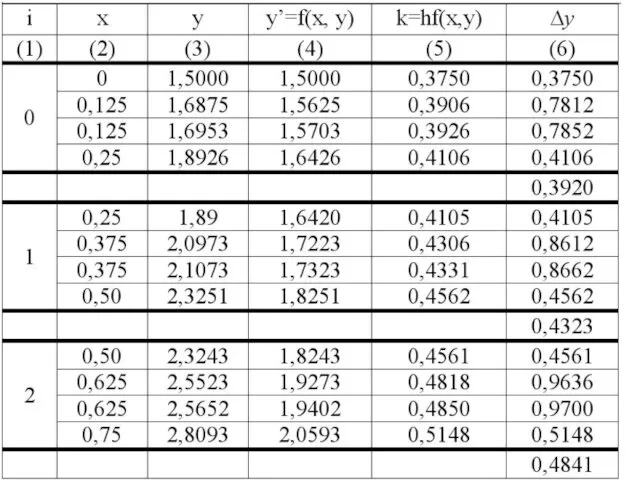
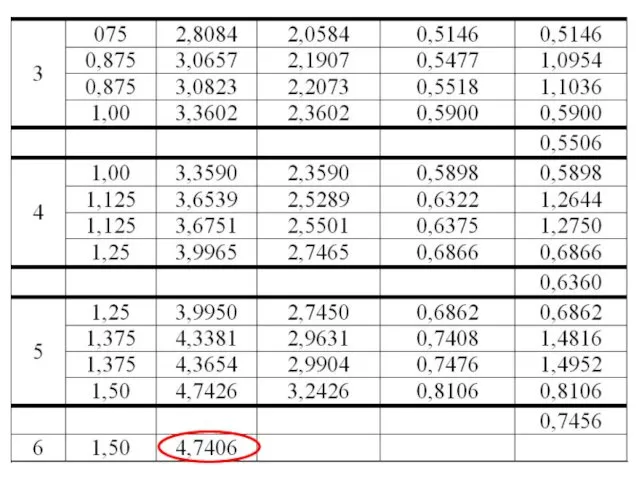
- 33. * Пример 1. Решить дифференциальное уравнение у′= у-x с начальным условием х0=0, у(х0)=у0=1.5 методом Рунге-Кутта. Вычислить
- 34. * k4(0)=[(y0+k3(0))-(x0+h)]h=[(1.5000+0.3926)- 0.125]*0.25=0.4106 =0,3920 y1=1.50000+0.3920=1.8920
- 35. *
- 36. *
- 37. * , Метод Рунге-Кутта при решении систем дифференциальных уравнений
- 38. * , где
- 39. *
- 40. *
- 41. *
- 42. * ,
- 43. * Метод последовательных приближений
- 44. * Первое приближение: Второе приближение: Третье приближение: … n-е приближение:
- 45. * Теорема. Пусть в окрестности точки (х0; у0) функция f(х, у) непрерывна и имеет ограниченную частную
- 46. * Оценка погрешности метода Пикара где М = mах |f(х, у)| N = mах |f ’y(х,
- 47. Метод Пикара последовательных приближений Дифференциальное уравнение n-ого порядка Рассмотрим дифференциальное уравнение первого порядка y’ = f(x,
- 48. Будем строить искомое решение y = y(x) для значений x ≥ x0. Случай x ≤ x0
- 49. Заменяя в равенстве (3) неизвестную функцию y данным значением y0, получим первое приближение Так как искомая
- 50. Далее подставив в равенстве (3) вместо неизвестной функции y найденную функцию y1, будем иметь второе приближение
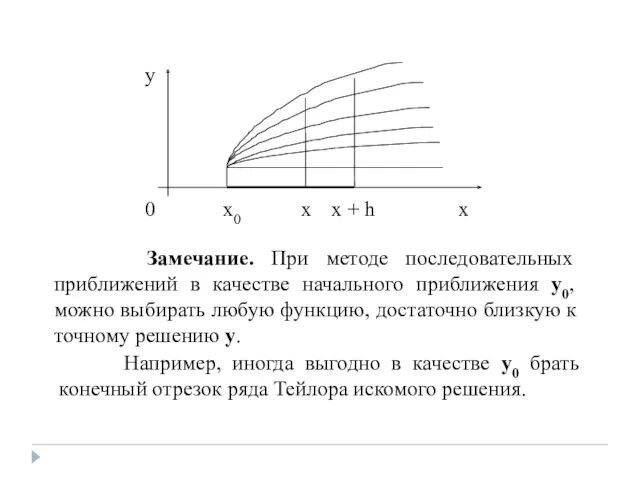
- 51. Замечание. При методе последовательных приближений в качестве начального приближения y0, можно выбирать любую функцию, достаточно близкую
- 52. Заметим, что при пользовании методом последовательных приближений аналитичность правой части дифференциального уравнения необязательна, поэтому этот метод
- 53. Решение. В качестве начального приближения возьмем y0(x) = 1. Так как то будем иметь Аналогично
- 54. Подобным же образом получим и т.д.
- 55. Система дифференциальных уравнений (метод Пикара) Дана система дифференциальных уравнений (4) где (5) Записывая векторное уравнение (4)
- 56. (6)
- 57. Этот метод годится также для дифференциального уравнения n-го порядка, если его записать в виде системы.
- 58. Пример 2. Построить несколько последовательных приближений для решения системы удовлетворяющего начальным условиям y1(0) = 1; y2(0)
- 59. Решение. Имеем: Отсюда, полагая получаем y1(0) = 1; y2(0) = 0
- 60. и т.д.
- 62. Скачать презентацию








![Постановка задачи Необходимо найти на отрезке [x0,xn] такую непрерывную функцию](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/111225/slide-9.jpg)






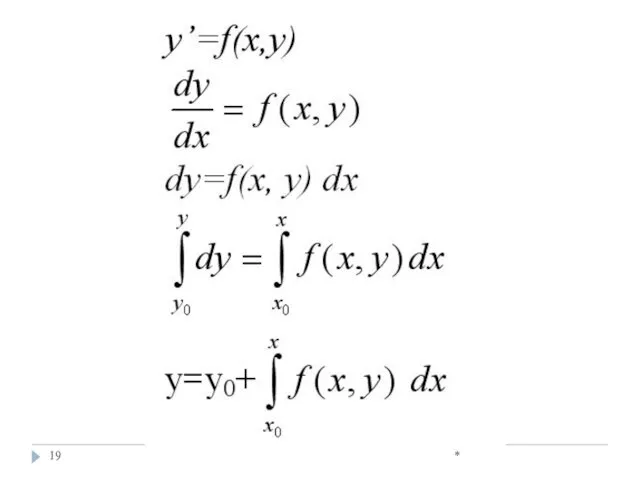
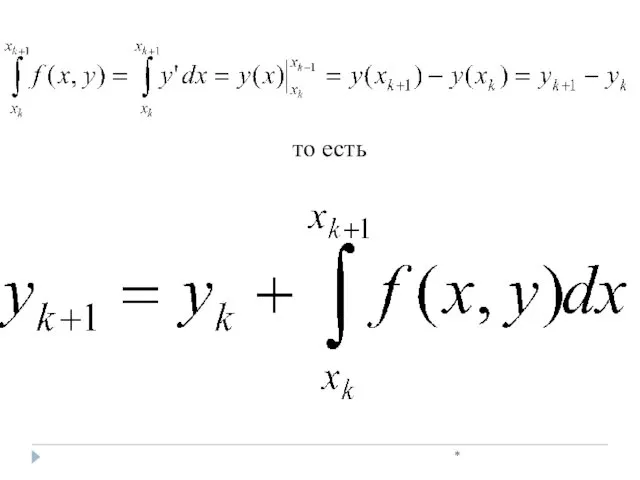
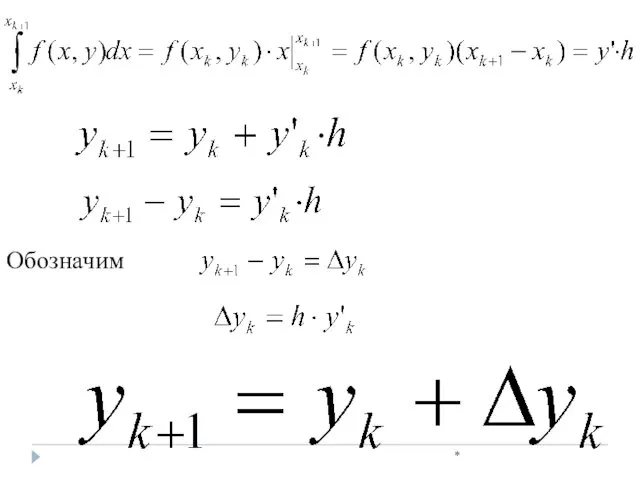

![* Пример 1. Решить у’=у-x с начальным условием х0=0, у0=1.5 на отрезке [0;1.5], h=0.25 Решение](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/111225/slide-23.jpg)



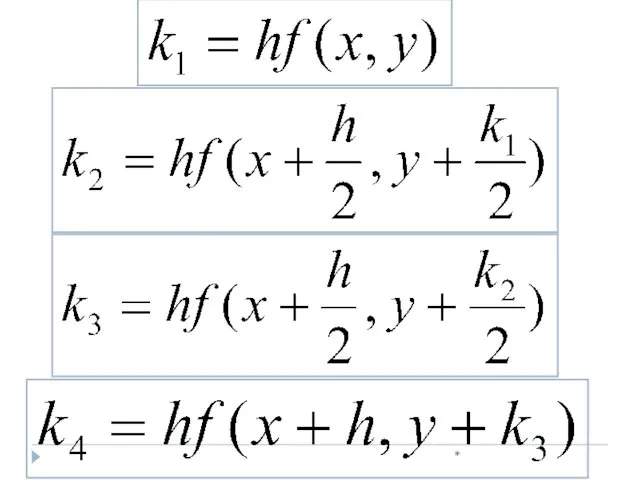
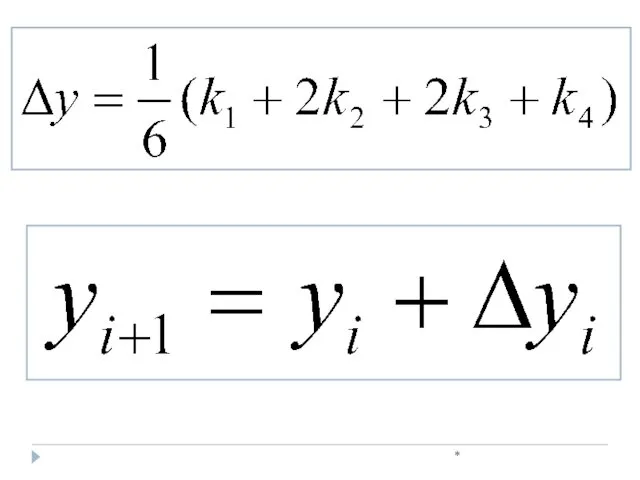


![* k4(0)=[(y0+k3(0))-(x0+h)]h=[(1.5000+0.3926)- 0.125]*0.25=0.4106 =0,3920 y1=1.50000+0.3920=1.8920](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/111225/slide-33.jpg)

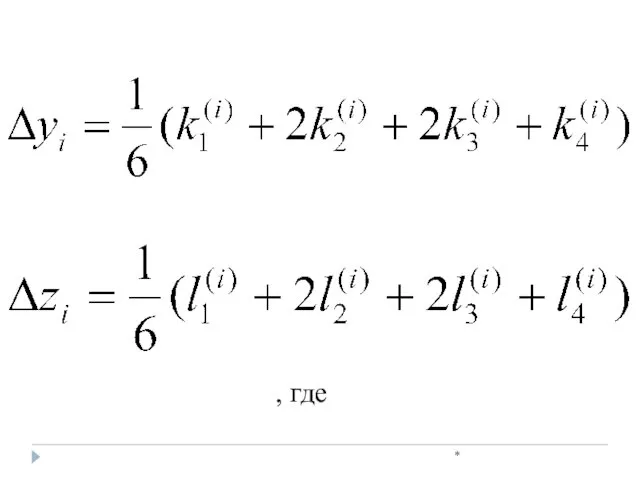
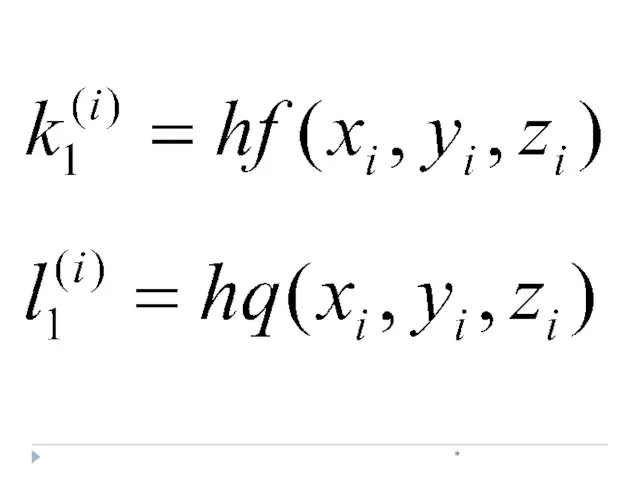
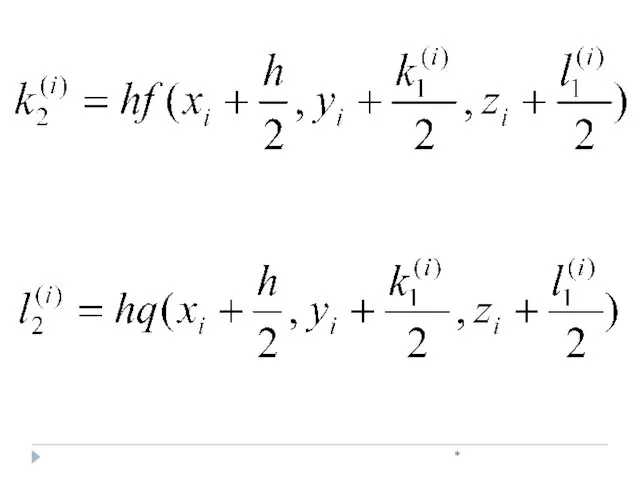
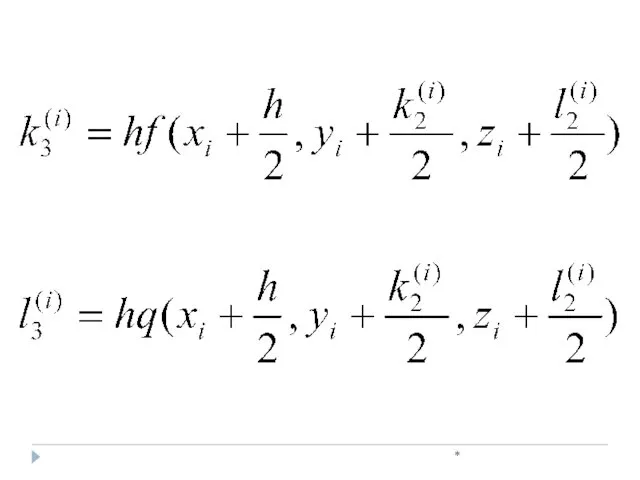
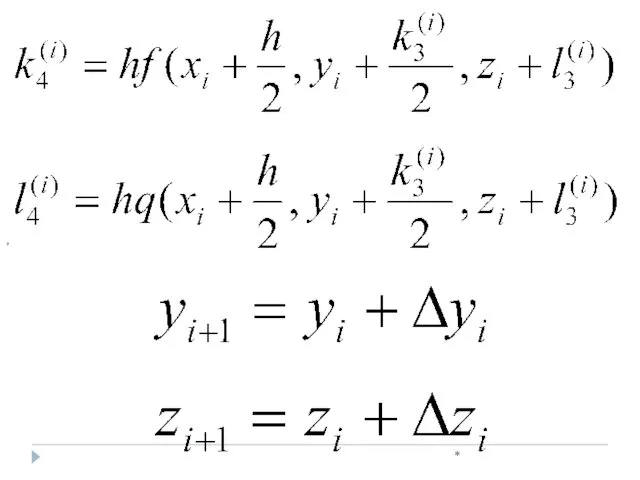
















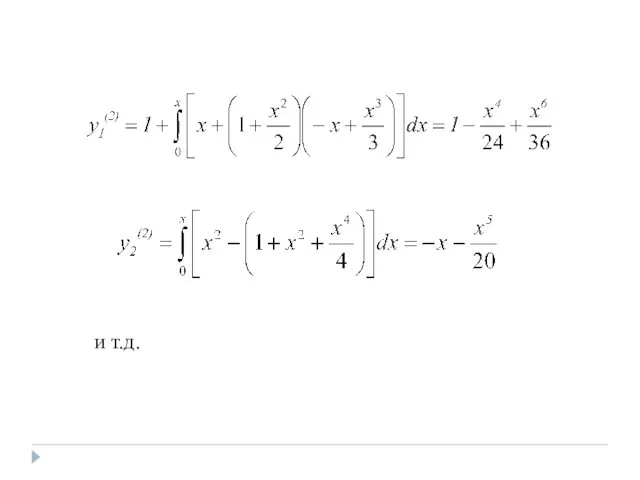
 Әй, осы математика
Әй, осы математика Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС
Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС Суміжні та вертикальні кути. Розв’язування задач
Суміжні та вертикальні кути. Розв’язування задач Конспект совместной деятельности педагога с детьми по математике во 2 младшей группе Путешествие в волшебную страну
Конспект совместной деятельности педагога с детьми по математике во 2 младшей группе Путешествие в волшебную страну Подобные слагаемые
Подобные слагаемые Линейная множественная регрессия
Линейная множественная регрессия Математика и здоровье
Математика и здоровье Пифагор Самосский
Пифагор Самосский Метод мажорант
Метод мажорант Устный счет. Задачи в стихах
Устный счет. Задачи в стихах Многочлен и его стандартный вид
Многочлен и его стандартный вид Презентация дидактических игр по математическомe развитию(младший дошкольный возраст)
Презентация дидактических игр по математическомe развитию(младший дошкольный возраст) Статистика. Основные этапы статистического анализа
Статистика. Основные этапы статистического анализа Информационные модели. Использование графов для решения задач
Информационные модели. Использование графов для решения задач Случаи вычитания 11-
Случаи вычитания 11- Система подготовки к ЕГЭ по математике
Система подготовки к ЕГЭ по математике Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Основные понятия теории графов. Тема 3
Основные понятия теории графов. Тема 3 Основы теории измерений. (Лекция 4)
Основы теории измерений. (Лекция 4) Дидактическая игра на уроке математики в 1 классе
Дидактическая игра на уроке математики в 1 классе Презентация Задачи с улыбкой
Презентация Задачи с улыбкой Устный счет в пределах 100 2 класс
Устный счет в пределах 100 2 класс Геометрическая интерпретация при решении уравнений, содержащих знак модуля
Геометрическая интерпретация при решении уравнений, содержащих знак модуля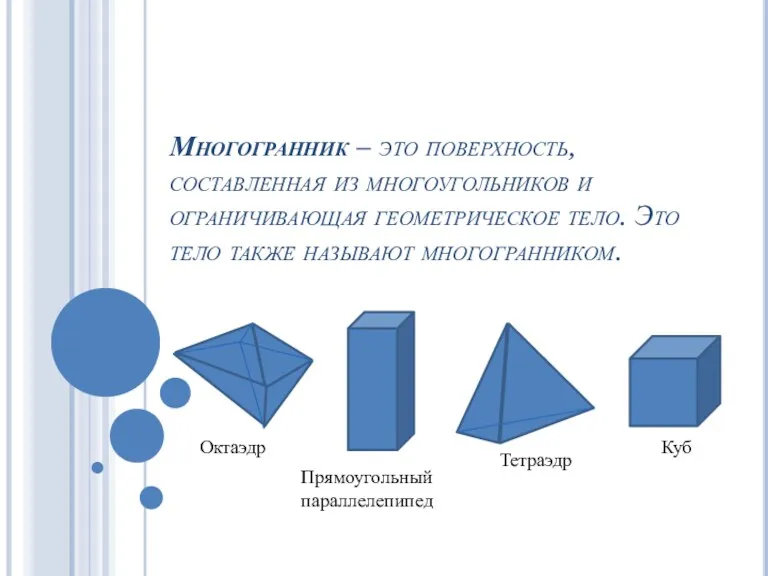 Многогранники и их виды
Многогранники и их виды О взаимосвязи начертательной геометрии и философии (презентация занятия для обучающихся в гр. №3)
О взаимосвязи начертательной геометрии и философии (презентация занятия для обучающихся в гр. №3) Аксиоматические системы и их свойства. Отношения между объектами
Аксиоматические системы и их свойства. Отношения между объектами Игра соревнование удачный выбор
Игра соревнование удачный выбор