Содержание
- 2. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют частным решением
- 3. Решить систему неравенств – значит найти все её частные решения, либо доказать , что у данной
- 4. Решение системы неравенств – это пересечение решений неравенств, входящих в систему. Запомните! Решение системы неравенств –
- 5. Алгоритм решения системы неравенств с одной переменной: 1. отдельно решить каждое неравенство; 2. найти пересечение найденных
- 6. Пример 1. Решить систему неравенств Решение. Отметим эти промежутки на координатной прямой. Решение первого неравенства помечено
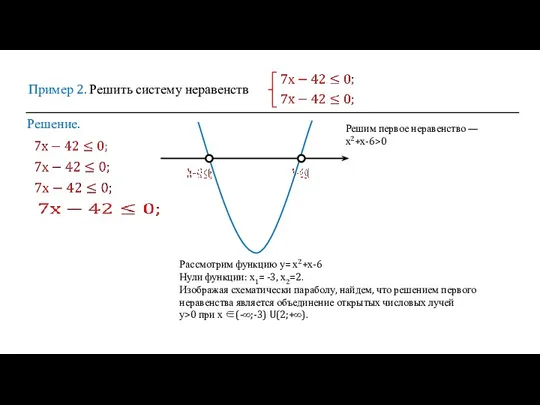
- 7. Пример 2. Решить систему неравенств Решение. Решим первое неравенство — х2+х-6>0 Рассмотрим функцию у= х2+х-6 Нули
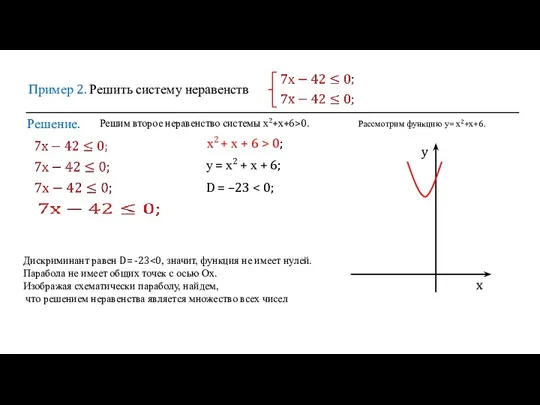
- 8. Пример 2. Решить систему неравенств Решение. х2 + х + 6 > 0; у = х2
- 9. Пример 2. Решить систему неравенств Решение. х2 + х + 6 > 0; у = х2
- 10. Пример 3. Решить систему неравенств log2(х2 – 13х + 42) ≥ 1. Решение. х2 – 13х
- 11. Говорят, что несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие
- 12. Каждое такое значение переменной называют частным решением совокупности неравенств.
- 13. Множество всех частных решений совокупности неравенств представляет собой общее решение совокупности неравенств. Запомните! Решение совокупности неравенств
- 14. Алгоритм решения совокупности неравенств: 1. отдельно решить каждое неравенство; 2. найти объединение найденных решений. Это объединение
- 15. Пример 4. Решить совокупность неравенств Решение. Решение Преобразуем каждое из неравенств. Получим равносильную совокупность неравенств Для
- 16. Пример 5. Решить совокупность неравенств Решение. (2; +∞); Ответ: (2; +∞). Преобразуем каждое из неравенств. Получим
- 17. Тема 12. Уравнения и неравенства 12.6. Решение неравенств с одной переменной. Иррациональные неравенства. Неравенства с модулем
- 18. Рассмотрим решение неравенства
- 19. 1. ОДЗ: f(х) ≥ 0; 2. g(х) > 0. При g(х) ≤ 0 неравенство не имеет
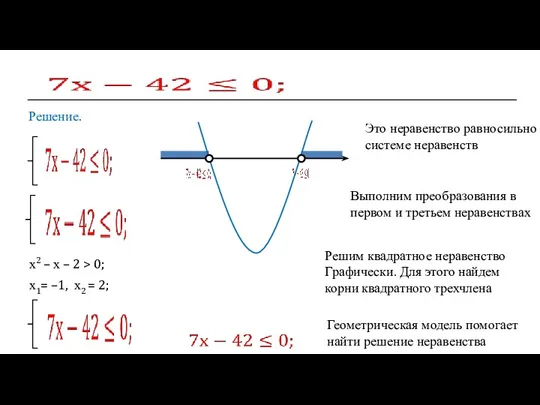
- 20. Решение. х2 – х – 2 > 0; х1= –1, х2 = 2; Это неравенство равносильно
- 21. Решение. х1= –2, х2 = 7; Это неравенство равносильно системе неравенств Выполним преобразования в каждом неравенстве
- 22. 3.
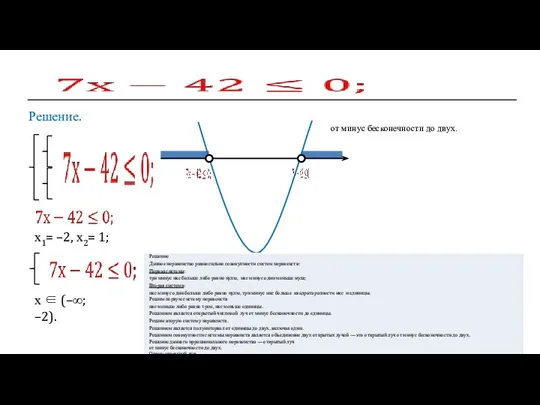
- 23. Решение. х ∈ (–∞; –2). х1= –2, х2= 1; от минус бесконечности до двух.
- 24. Решение. х ∈ (2; +∞); х ∈ (–∞; –2); х1= –2, х2= 1; Данное неравенство равносильно
- 25. Тема 12. Уравнения и неравенства 12.7. Решение систем уравнений второй степени https://youtu.be/9uV7TPwLpTI
- 26. Рассмотрим сначала системы уравнений с двумя переменными, составленные из одного уравнения второй степени и одного уравнения
- 27. Для этого выполняют следующий алгоритм действий: — выражают из уравнения первой степени одну переменную через другую;
- 28. Пример 1: Решить систему уравнений Решение: Ответ: (-1, 25; 0,75); (1,6; -0,2) Выразим из второго уравнения
- 29. Если система состоит из двух уравнений второй степени с двумя переменными, то найти её решения обычно
- 30. Пример 2: Решить систему уравнений Решение: Ответ: (-2; -1); (2; 1) x ≠ 0
- 31. Тема 12. Уравнения и неравенства 12.8. Системы уравнений https://youtu.be/RJg-GrAcv10
- 32. Метод подстановки; метод алгебраического сложения; метод введения новых переменных; графический метод. Для решения систем уравнений с
- 33. Если поставлена задача – найти такие пары (х; у), которые одновременно удовлетворяют уравнению р(х; у) =
- 34. Пару значений (х; у), которая одновременно является решением и первого и второго уравнения системы, называют решением
- 35. Решить систему уравнений – значит найти все её решения или установить, что решений нет.
- 36. р(х; у; z) =0 q(х; у; z) =0 r(х; у; z) =0 Система трех уравнений с
- 37. Алгоритм решения системы уравнений постепенный переход от сложного уравнения к более простому, но при этом выполнять
- 38. Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не
- 39. метод подстановки; метод алгебраического сложения; введения новых переменных. Равносильные способы решения систем уравнений:
- 40. возведение в квадрат обеих частей уравнения; умножение уравнений системы; преобразования, приводящие к расширению области определения. Проверка
- 41. Пример 1. Решить систему уравнений х + у + 2z = 4, 2х + у +
- 42. Пример 2. Решить систему уравнений х + у = 1, log3х = log3(1 – у). Решение.
- 43. Пример 3. Решить систему уравнений Решение. (1; 1), (–1; –1);
- 44. Задание 3 Решить систему уравнений: игрек квадрат плюс два икс игрек минус три икс квадрат равно
- 45. Пример 4. Решить систему уравнений Решение. Ответ: (1; 0). (1; 0), (–2; 3); х = –2,
- 47. Скачать презентацию







































 Решение задач. Составить выражение к задаче
Решение задач. Составить выражение к задаче логические задачи
логические задачи Скобки в числовом выражении
Скобки в числовом выражении Округление десятичных чисел
Округление десятичных чисел Урок 39. Сумма и произведение. Знак умножения.
Урок 39. Сумма и произведение. Знак умножения. Көрсеткіштік теңдеулердің
Көрсеткіштік теңдеулердің Параллельный перенос. Симметрия
Параллельный перенос. Симметрия Авторская мультимедийная игра На что похоже для детей старшего дошкольного возраста.
Авторская мультимедийная игра На что похоже для детей старшего дошкольного возраста. Обыкновенные дроби
Обыкновенные дроби Квадратные уравнения. Решение неполных квадратных уравнений
Квадратные уравнения. Решение неполных квадратных уравнений Тераэдр, параллелепипед
Тераэдр, параллелепипед Порядок действий в выражениях
Порядок действий в выражениях Простые задачи на увеличение числа на несколько единиц
Простые задачи на увеличение числа на несколько единиц Устный счёт к уроку Многозначные числа.Математика. Т.Е.Демидова. 3 класс. Школа 2100.
Устный счёт к уроку Многозначные числа.Математика. Т.Е.Демидова. 3 класс. Школа 2100. Задание В8, открытого банка ЕГЭ по математике
Задание В8, открытого банка ЕГЭ по математике Лекции по теории функции комплексной переменной
Лекции по теории функции комплексной переменной Курс лекций по математике
Курс лекций по математике Математика в сказках. Интегрированный урок по математике и литературе
Математика в сказках. Интегрированный урок по математике и литературе Устный счет по математике
Устный счет по математике Координатная ось
Координатная ось Разложение многочлена на множители способом группировки
Разложение многочлена на множители способом группировки Алгоритмы на графах
Алгоритмы на графах Метод координат. Геометрия 9 класс
Метод координат. Геометрия 9 класс Сложения вида +4
Сложения вида +4 Разность квадратов
Разность квадратов Логарифмы и их свойства
Логарифмы и их свойства Вечер весёлых задач
Вечер весёлых задач Сыбайлас және вертикаль бұрыштар
Сыбайлас және вертикаль бұрыштар