Содержание
- 2. Лекция № 1 §1. Комплексные числа и последовательности комплексных чисел. п. 1. Понятие комплексного числа. Геометрическая
- 3. -вектор Определим операцию сложения: Рассмотрим плоскость R2.
- 4. операцию умножения на число: базис Как ввести
- 5. Вектор 1– единица операции умножения. Определим Т.к. то полагают
- 6. Правило умножения Def. Числовая плоскость называется комплексной плоскостью C, если для ее точек определены модули (1),
- 7. Действительные числа включаются в множество комплексных чисел. a=(a,0)-вещественное число, -1=(-1, 0), i =(0, 1)- мнимая единица,
- 8. Деление. Комплексное сопряжение.
- 9. Примеры.
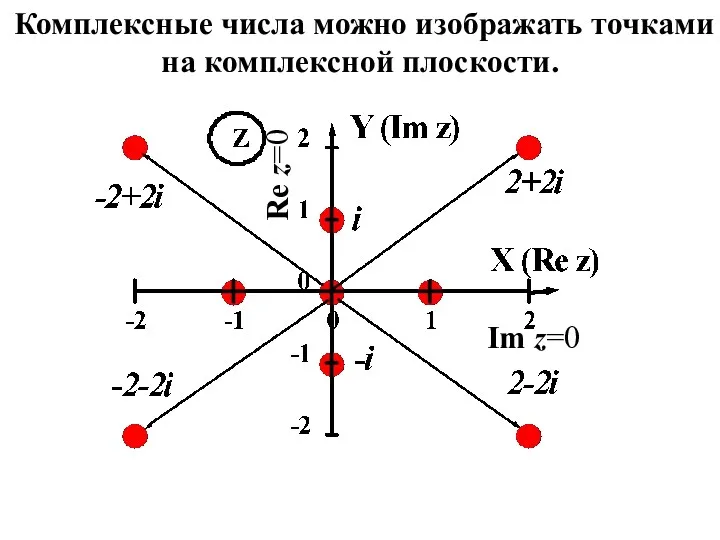
- 10. Комплексные числа можно изображать точками на комплексной плоскости. Im z=0 Re z=0
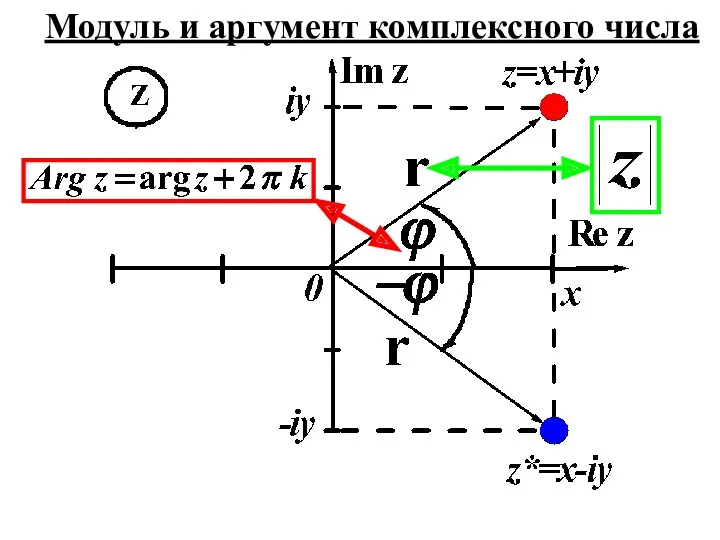
- 11. Модуль и аргумент комплексного числа
- 12. Полярные координаты (x,y)↔(r,ϕ). Модуль комплексного числа: Аргумент комплексного числа: Главное значение аргумента.
- 13. -разрез по -разрез по Примеры. — не определен!
- 14. Тригонометрическая форма записи формула Эйлера: Показательная форма записи Теорема.1.1. Пусть тогда
- 15. Примеры.
- 16. Вопрос. Умножение и деление в показательной форме. Формула Муавра.
- 17. Извлечение корня. Корень n-той степени из комплексного числа принимает n различных значений.
- 18. Примеры.
- 22. Операция сравнения в С не определена. Множество комплексных чисел C образует поле. Поле С не является
- 23. Неравенства треугольника. Упорядоченная четверка является нормированным векторным пространством над полем R. Оно превратится в метрическое пространство,
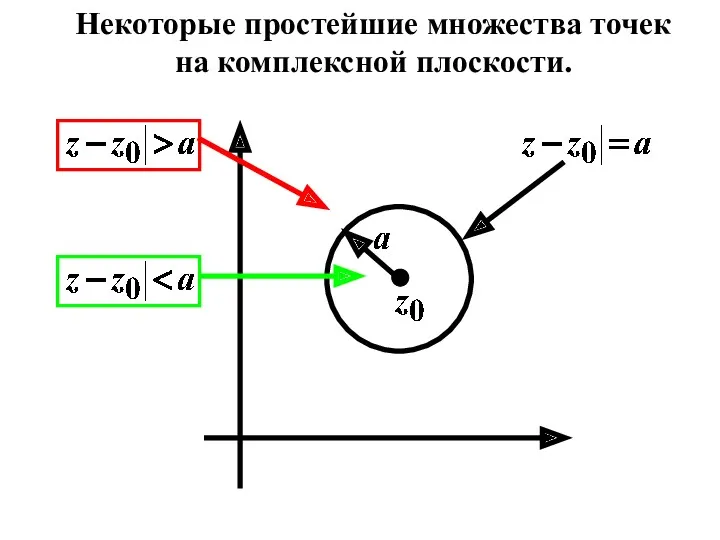
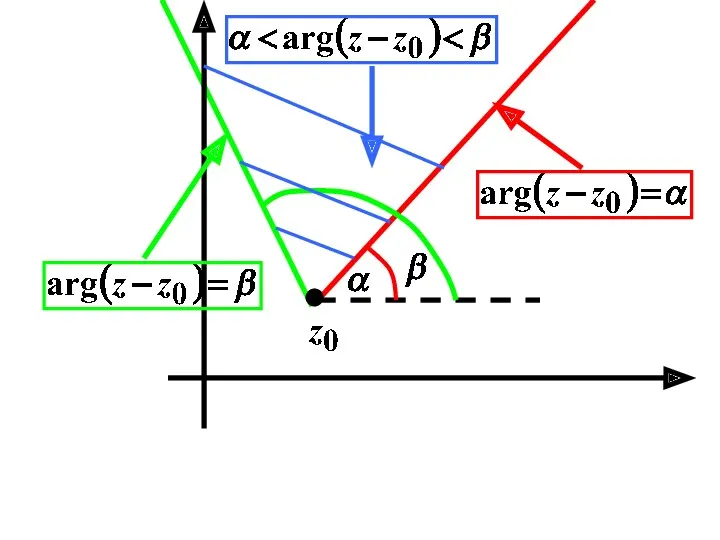
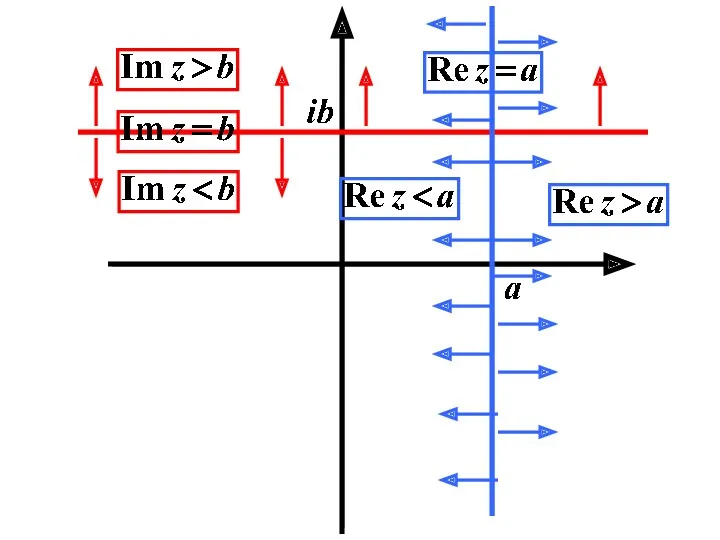
- 24. Некоторые простейшие множества точек на комплексной плоскости.
- 27. Def. Последовательностью комплексных чисел называют упорядоченное счетное множество комплексных чисел. Члены последовательности располагаются в порядке следования
- 28. Примеры. не существует Каждый член последовательности Т.1.2. Необходимым и достаточным условием является требование сходимости
- 29. Def. Последовательность называется ограниченной, если Сходящаяся последовательность ограничена. Критерий Коши. Необходимым и достаточным является условием сходимости
- 30. Def. Если для то последовательность называется неограниченно возрастающей. Примеры. Неограниченно возрастающие последовательности.
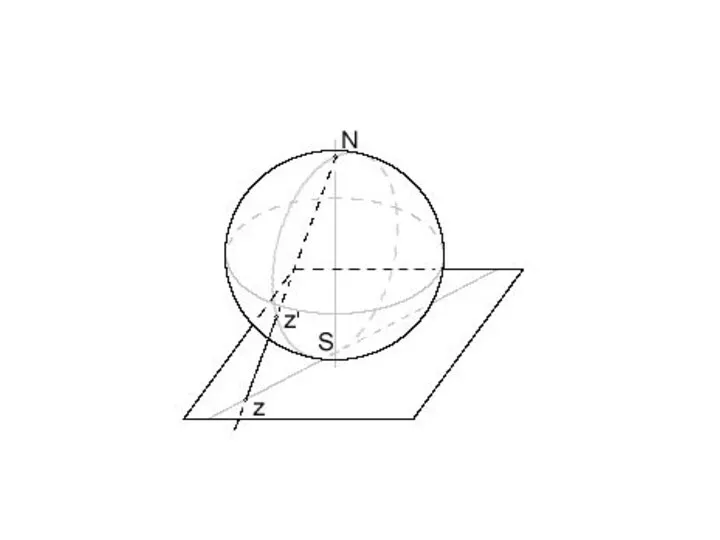
- 31. Все неограниченно возрастающие последовательности сходятся к единственной бесконечно удаленной точке комплексной плоскости. Def. Комплексная плоскость дополненная
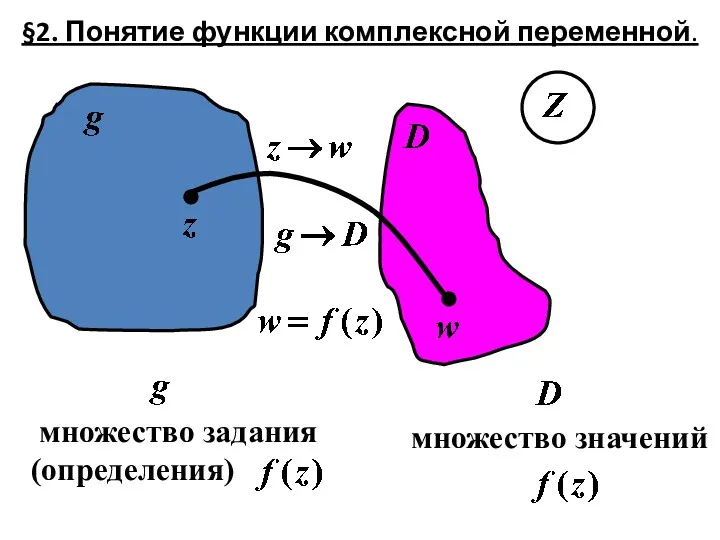
- 33. §2. Понятие функции комплексной переменной. множество задания (определения) множество значений
- 34. Точки множества. Def. Точка называется внутренней точкой множества если Def. Множество, состоящее из внутренних точек называется
- 35. Def. Множество называется связным, если можно соединить кусочно-гладкой кривой Def. Область— открытое, связное множество. Def. Точка
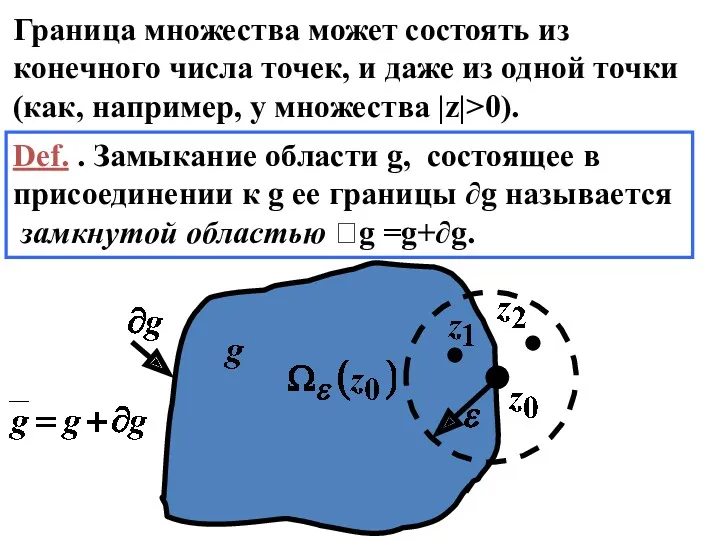
- 36. Граница множества может состоять из конечного числа точек, и даже из одной точки (как, например, у
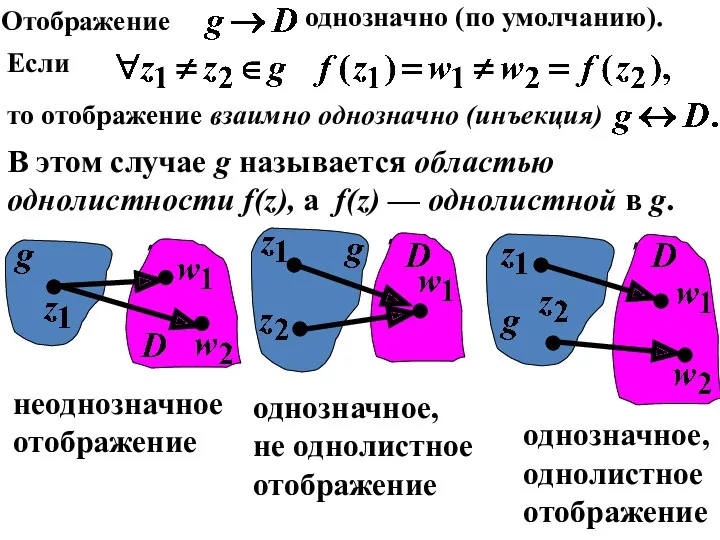
- 37. Отображение однозначно (по умолчанию). Если то отображение взаимно однозначно (инъекция) В этом случае g называется областью
- 38. При z=x+iy, w= f(z)=u(x,y)+iv(x,y). Свойства функции комплексной переменной определяются свойствами функций двух действительных переменных. При g↔D
- 39. Некоторые элементарные функции комплексной переменной. Однозначная, однолистная на всей комплексной плоскости. Геометрический смысл: растяжение в k
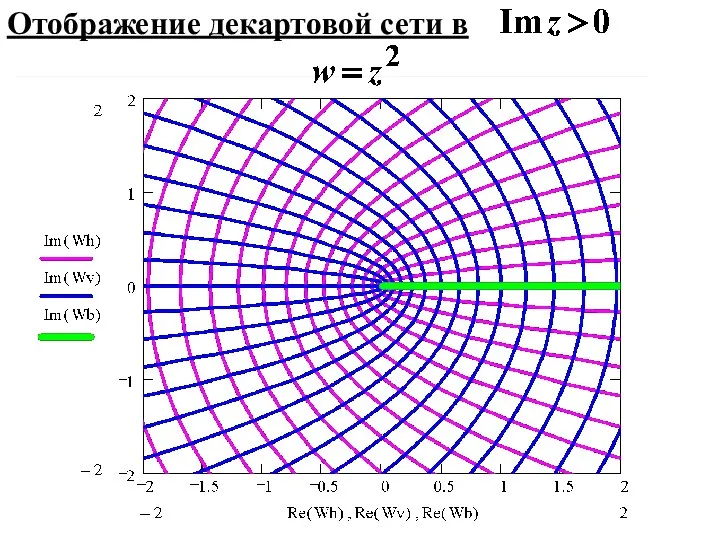
- 40. Однозначная, но не однолистная на всей комплексной плоскости. Область однолистности— полуплоскость Область однолистности отображается на всю
- 41. Декартова сеть
- 42. Отображение декартовой сети в
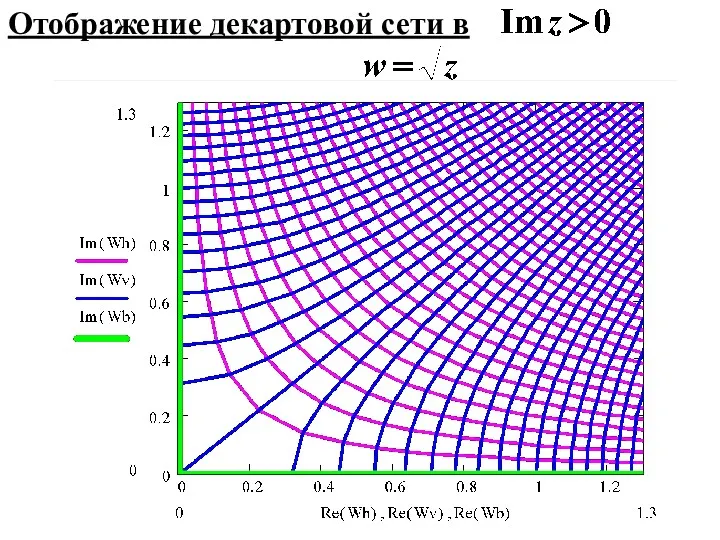
- 43. Две ветви: Точки ветвления, при обходе которых по любому замкнутому контуру происходит переход с одной ветви
- 44. Отображение декартовой сети в
- 45. Однозначная, однолистная на всей комплексной плоскости. Геометрический смысл: симметричное отражение относительно вещественной оси и инверсия относительно
- 47. Скачать презентацию











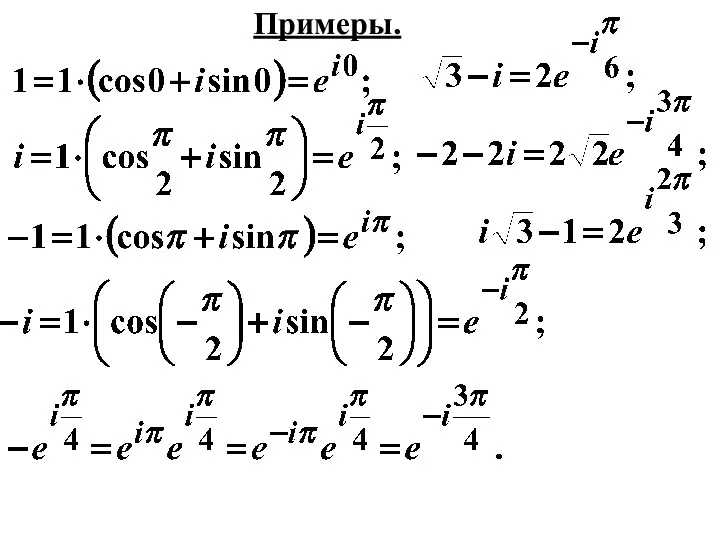



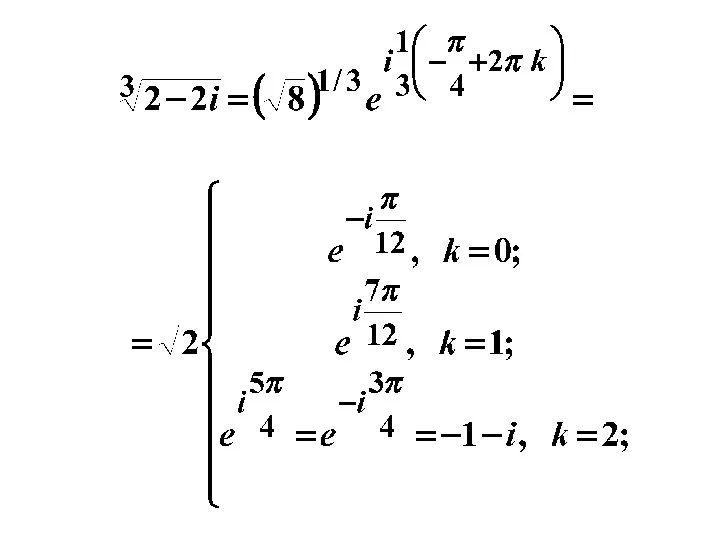
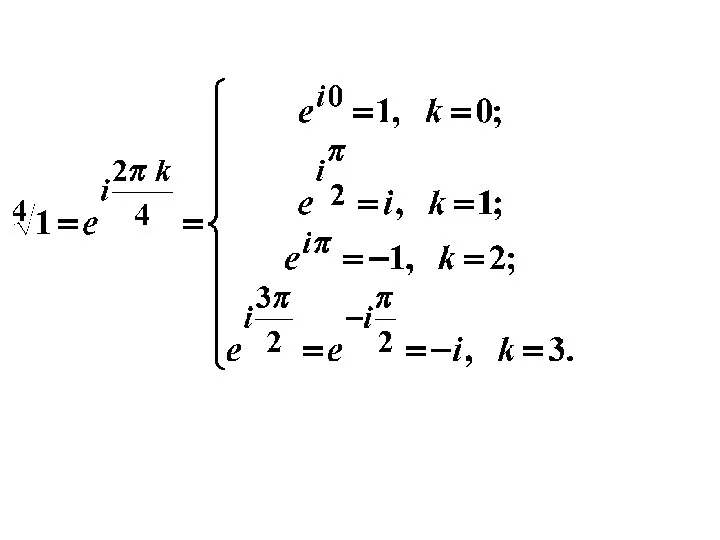
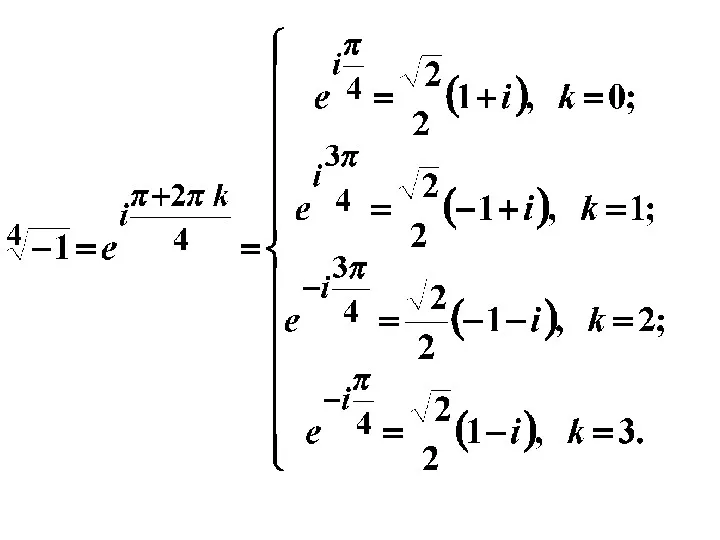














 Из опыта работы с проектной задачей.
Из опыта работы с проектной задачей. Тест по математике для 1 класса (программа Школа 2100)
Тест по математике для 1 класса (программа Школа 2100) Математический диктант_1 класс
Математический диктант_1 класс Знания имей отличные по теме дроби десятичные
Знания имей отличные по теме дроби десятичные Примеры заданий по математике, выполнение которых предполагают развитие творческих способностей младших школьников в процессе формирования математических представлений и понятий
Примеры заданий по математике, выполнение которых предполагают развитие творческих способностей младших школьников в процессе формирования математических представлений и понятий Проверка гипотез, относящихся к коэффициентам регрессии
Проверка гипотез, относящихся к коэффициентам регрессии Решение задач на нахождение неизвестного третьего слагаемого. 2 класс
Решение задач на нахождение неизвестного третьего слагаемого. 2 класс Геометрия. Площади многоугольников
Геометрия. Площади многоугольников Игра для урока математики
Игра для урока математики Пропорции. Равные отношения
Пропорции. Равные отношения Урок математики по теме Длина ломаной. Периметр с презентацией
Урок математики по теме Длина ломаной. Периметр с презентацией Решение задач и выражений
Решение задач и выражений Математика. 1 класс. Урок 2. Форма
Математика. 1 класс. Урок 2. Форма Делители и кратные
Делители и кратные Стандартизация статистических показателей
Стандартизация статистических показателей Аналитическая геометрия на плоскости
Аналитическая геометрия на плоскости Функции и их графики
Функции и их графики Статистика бюджета. Экономические модели
Статистика бюджета. Экономические модели Параллелограмм и его свойства
Параллелограмм и его свойства Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби Квадратные уравнения. Из истории
Квадратные уравнения. Из истории Геометрия и стереометрия
Геометрия и стереометрия Вычисления, упрощения с корнями
Вычисления, упрощения с корнями Промежутки возрастания и убывания функции
Промежутки возрастания и убывания функции Цилиндр. Решение задач
Цилиндр. Решение задач Розв’язування тригонометричних рівнянь
Розв’язування тригонометричних рівнянь Функция. Способы задания функций
Функция. Способы задания функций