Содержание
- 2. Прямая и плоскость пересекаются, если они имеют одну единственную общую точку, которую называют точкой пересечения прямой
- 3. Проекцией точки М на плоскость α называется либо сама точка М, если М лежит в плоскости
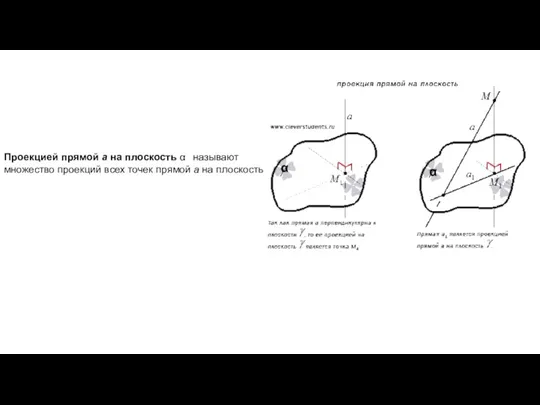
- 4. Проекцией прямой a на плоскость α называют множество проекций всех точек прямой a на плоскость .
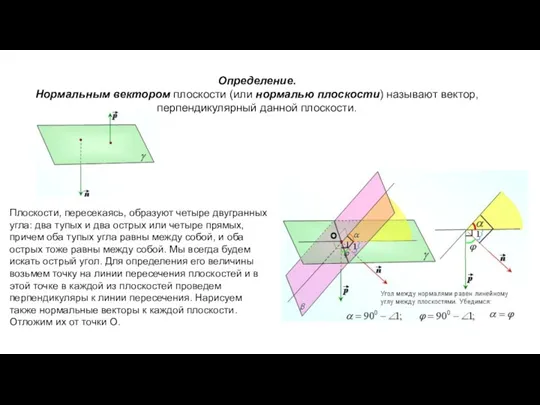
- 6. Определение. Нормальным вектором плоскости (или нормалью плоскости) называют вектор, перпендикулярный данной плоскости. Плоскости, пересекаясь, образуют четыре
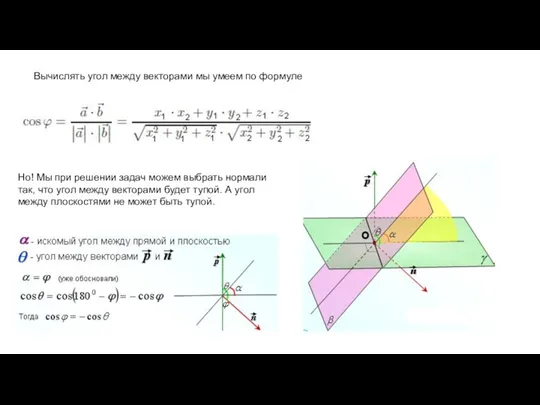
- 7. Вычислять угол между векторами мы умеем по формуле Но! Мы при решении задач можем выбрать нормали
- 8. Итак, если угол между нормалями острый, то мы сразу получаем угол между плоскостями (формула со знаком
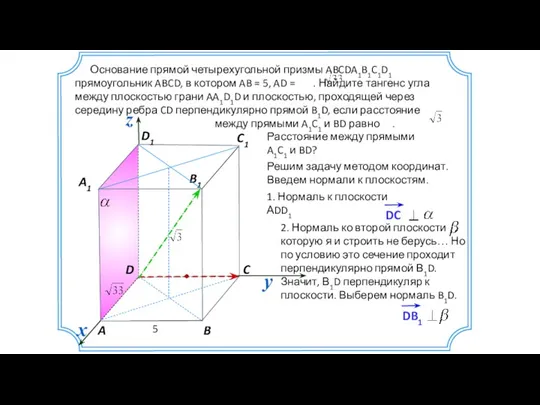
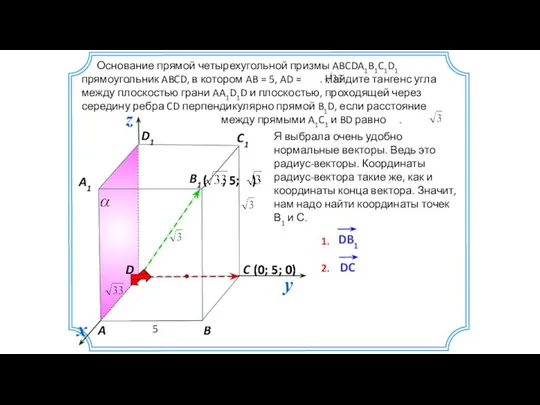
- 10. Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 5, AD = . Найдите
- 11. (0; 5; 0) Основание прямой четырехугольной призмы ABCDA1B1C1D1 прямоугольник ABCD, в котором AB = 5, AD
- 13. Скачать презентацию





 Умножение 7 и на 7
Умножение 7 и на 7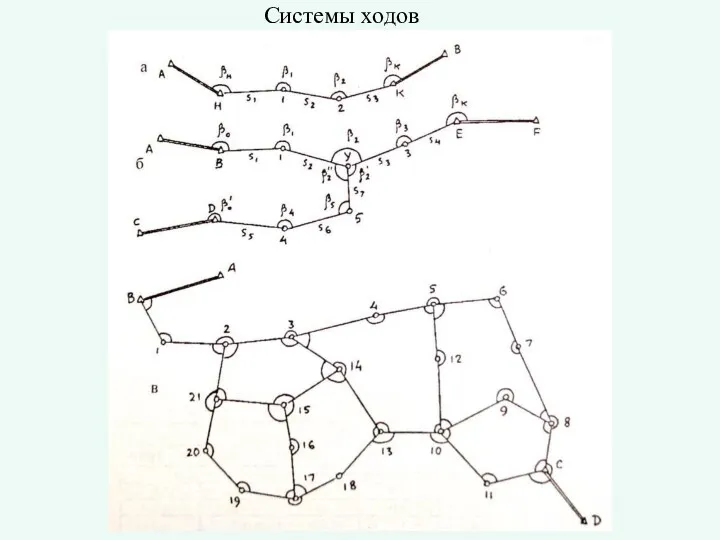 Системы ходов. Виды теодолитных ходов
Системы ходов. Виды теодолитных ходов Урок математики в 3 классе
Урок математики в 3 классе Система обобщающего повторения на уроках геометрии при подготовке к ГИА
Система обобщающего повторения на уроках геометрии при подготовке к ГИА Математические модели в экономике
Математические модели в экономике Именованные числа. Тренажёр
Именованные числа. Тренажёр Применение производной к решению экономических задач
Применение производной к решению экономических задач Вероятность события
Вероятность события Чтение многозначных чисел
Чтение многозначных чисел Признаки делимости на 3 и 9
Признаки делимости на 3 и 9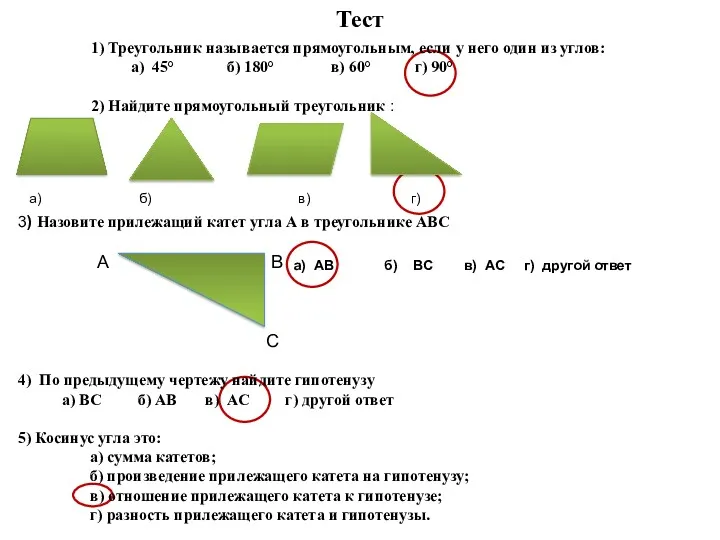 Тест. Прямоугольный треугольник
Тест. Прямоугольный треугольник Система старинных русских мер
Система старинных русских мер Интегрированное занятие по ФЭМП в средней группе
Интегрированное занятие по ФЭМП в средней группе Инвариантность систем
Инвариантность систем Сравнение десятичных дробей
Сравнение десятичных дробей Нахождение площади и периметра
Нахождение площади и периметра Теорема Фалеса 1
Теорема Фалеса 1 Алгебра логики. Контрольная работа
Алгебра логики. Контрольная работа Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Секреты умножения и деления
Секреты умножения и деления Производная в биологии и химии
Производная в биологии и химии Основыне понятия теории погрешностей
Основыне понятия теории погрешностей Запись и чтение чисел второго десятка
Запись и чтение чисел второго десятка Решение задач на движение
Решение задач на движение Предел функции на бесконечности
Предел функции на бесконечности Определитель. Линейная алгебра
Определитель. Линейная алгебра Составляем и решаем задачи
Составляем и решаем задачи По страницам учебника математики (8 класс)
По страницам учебника математики (8 класс)