Таку систему рівнянь називають східчастою або трапецієподібною. Дослідимо цю систему.
1. Якщо
система містить рівняння виду 0=bt i bt≠0 то вона несумісна.
2. Нехай система (14) не містить рівнянь виду 0=bt i bt≠0 Назвемо невідомі x1,xk,xi,…,x5 з яких починаються перше, друге, ..., r - е рівняння, основними, а всі інші, якщо вони є, вільними. Основних невідомих за означенням r. Надаючи вільним невідомим довільні значення і підставляючи ці значення в рівняння системи, з r - го рівняння знайдемо x5. Підставляючи це значення в перші r - 1 рівнянь і, піднімаючись вгору по системі, знайдемо всі основні невідомі. Оскільки вільні невідомі можуть набувати будь-яких значень, система має безліч розв’язків.
3. Нехай в системі (14) r=n Тоді вільних невідомих немає, тобто всі невідомі основні і система (14) має так званий трикутний вигляд:
З останнього рівняння системи знайдемо xn і, піднімаючись по системі вгору, знайдемо всі інші невідомі. Отже, в цьому випадку система має єдиний розв’язок.













 Область определения и область значений функции
Область определения и область значений функции Параллелограмм
Параллелограмм Тема урока: числа от 1 до 8
Тема урока: числа от 1 до 8 ВПМ. Математичне програмування та дослідження операцій. Оптимізаційні задачі управління запасами. (Лекція 5)
ВПМ. Математичне програмування та дослідження операцій. Оптимізаційні задачі управління запасами. (Лекція 5) Сложение и вычитание смешанных чисел. Устный счет. Открытый урок. 5 класс
Сложение и вычитание смешанных чисел. Устный счет. Открытый урок. 5 класс Таблица умножения в кроссвордах
Таблица умножения в кроссвордах Алгоритм сложения и вычитания трёхзначных чисел
Алгоритм сложения и вычитания трёхзначных чисел Урок математики в 4 классе Белгородчина - жемчужина России
Урок математики в 4 классе Белгородчина - жемчужина России Умножение разности двух выражений на их сумму
Умножение разности двух выражений на их сумму Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация
Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация Смешанные числа. Математика — царица наук
Смешанные числа. Математика — царица наук Учебники математики
Учебники математики Графики и диаграммы. ЕГЭ-2012. Решение задач В2
Графики и диаграммы. ЕГЭ-2012. Решение задач В2 Смешанные числа. Задачи
Смешанные числа. Задачи Случайные события. Вероятность события
Случайные события. Вероятность события Урок закрепление по теме Числа от 1до 10.
Урок закрепление по теме Числа от 1до 10. Формулы сокращённого умножения
Формулы сокращённого умножения Штангенциркуль
Штангенциркуль Информационно-исследовательский проект Магический куб
Информационно-исследовательский проект Магический куб Розв’язування тригонометричних рівнянь
Розв’язування тригонометричних рівнянь Прибавление и вычитание числа 4 Математика 1 класс
Прибавление и вычитание числа 4 Математика 1 класс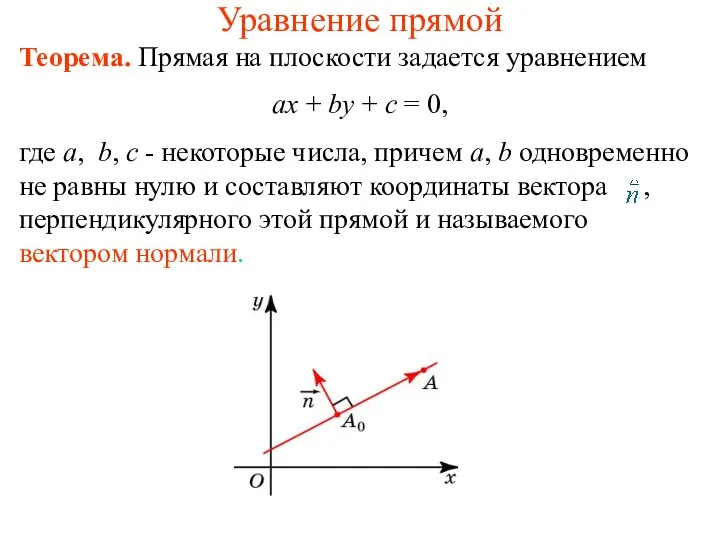 Уравнение прямой
Уравнение прямой Счет в пределах 10, 1 класс Зимние забавы
Счет в пределах 10, 1 класс Зимние забавы Функция графигінің асимптоталары
Функция графигінің асимптоталары Определение синуса, косинуса, тангенса и котангенса
Определение синуса, косинуса, тангенса и котангенса методическая разработка урока математики Единицы времени.Век
методическая разработка урока математики Единицы времени.Век Презентация младшая группа Дидиктическая игра Подбери форму Диск
Презентация младшая группа Дидиктическая игра Подбери форму Диск Случаи сложения вида +8, +9. Таблица сложения
Случаи сложения вида +8, +9. Таблица сложения