Содержание
- 2. 1. Общее понятие СОУ. При исследовании экономических про-цессов для их описания не всегда достаточно только одного
- 3. Выделяют следующие три вида экономет-рических систем уравнений: система независимых уравнений, когда каждая зависимая переменная рассмат-ривается как
- 5. система одновременных (взаимозави-симых) уравнений (СОУ), когда зависимые переменные в одних уравнениях входят в левую часть системы,
- 6. В рассмотренных первых двух видах систем каждое уравнение этих систем может рассматриваться самостоятельно, отдельно, и для
- 7. Например, если изучается модель спроса, как соотношение цены и количества потре-бляемых товаров, то одновременно для про-гнозирования
- 8. где спрос, предложение, цена товара, доход потребителя. Уравнение (3) показывает, что рынок находится в состоянии равновесия
- 9. Переменные и формируют свои значе-ния, подчиняясь уравнениям (1) и (2), т.е. внутри модели. Такие переменные в
- 10. Эндогенные переменные в системе одновременных уравнений, записанной в общем виде, обозначаются символом , а экзогенные -
- 11. Как уже отмечалось в СОУ одни и те же переменные одновременно рассматривают-ся как зависимые в одних
- 12. Простейшая структурная форма модели с двумя эндогенными и двумя экзогенными переменными имеет вид: Использование МНК для
- 13. Оценивание структурных коэффициентов СОУ требует специальных методов. Одним из них является косвенный метод наимень-ших квадратов (КМНК),
- 14. 2. Косвенный метод наименьших квадратов. Косвенный метод наименьших квадратов включает три шага: 1) получение приведенной формы
- 15. 2) применение обычного МНК к каж-дому независимому уравнению приведенной формы и получение точечных оценок коэф-фициентов приведенной
- 16. Первый шаг. Выразим из уравнения (4): Приравнивая правые части полученного соотношения и уравнения (5), после несло-жных
- 17. Если ввести обозначения то получим уравнение Выполняя аналогичные преобразования с переменной из уравнения (5), можно получить:
- 18. Система уравнений (7), (8) представляет приведенную форму модели, так как эндо-генные переменные модели выражены толь-ко через
- 19. Второй шаг. Для получения оценок коэ-ффициентов приведенной формы МНК требуются статистические данные в виде многомерной выборки:
- 20. На основании этих данных находятся оценки коэффициентов приведенной формы для каждого уравнения отдельно. Например, оценка найдется
- 21. Третий шаг. Заменяя в равенствах (6), (9) коэффициенты полученными на втором шаге их оценками , после
- 22. 3. Проблема идентифицируемости. Экономический смысл и интерес для анализа представляют только структурные коэффициенты модели. Однако переход
- 23. Идентифицируемость - это единствен-ность соответствия между приведенной и структурной формами модели. С позиции идентифицируемости струк-турные формы
- 24. В первом случае все структурные коэф-фициенты однозначно, единственным обра-зом определяются через коэффициенты при-веденной формы. Число коэффициентов
- 25. Наконец, в последнем случае число ко-эффициентов приведенной формы превы-шает число коэффициентов структурной формы, и они определяются
- 26. Если хотя бы одно уравнение сверх-идентифицируемо, то и вся модель считается сверхидентифицируемой. Для структурной формы модели
- 27. число предопределенных переменных в м уравнении системы; матрица коэффициентов при пере-менных (всех типов), не входящих в
- 28. если выполняется равенство то уравнение идентифицируемо; если выполняется неравенство то уравнение сверхидентифицируемо; если выполняется неравенство то
- 29. Достаточное условие идентифицируе-мости го уравнения системы: Для того чтобы е уравнение системы было идентифицируемо достаточно, чтобы
- 30. 2. Если и ранг матрицы равен ( ), то уравнение идентифици-руемо. 3. Если и ранг матрицы
- 31. 4. Двухшаговый метод наименьших квадратов. Если СОУ сверхидентифицируема, то КМНК не используется, ибо он не даёт
- 32. Алгоритм ДМНК включает следующие шаги: 1. Получение приведённой формы модели. 2. Применение обычного МНК к каждому
- 33. 4. Определение оценок структурных коэф-фициентов каждого уравнения в отдельности обычным МНК, используя в качестве факто-ров входящие
- 34. Рассмотрим применение ДМНК на при-мере системы (4)-(5): Первый шаг. Получаем приведенную форму (см. пункт 2 лекции):
- 35. Второй шаг. Для оценки коэффициентов уравнений приведенной формы используем статистические данные таблицы 1. В результате получаем
- 36. Третий шаг. В правые части исходной структурной формы входят в качестве объя-сняющих обе эндогенные переменные .
- 37. Четвёртый шаг. Для определения оценок первого уравнения структурной формы испо-льзуем обычный МНК с данными, взятыми из
- 38. В результате получаем уравнение регрессии Аналогично по исходным данным . 1 … … … … оцениваются
- 40. Скачать презентацию


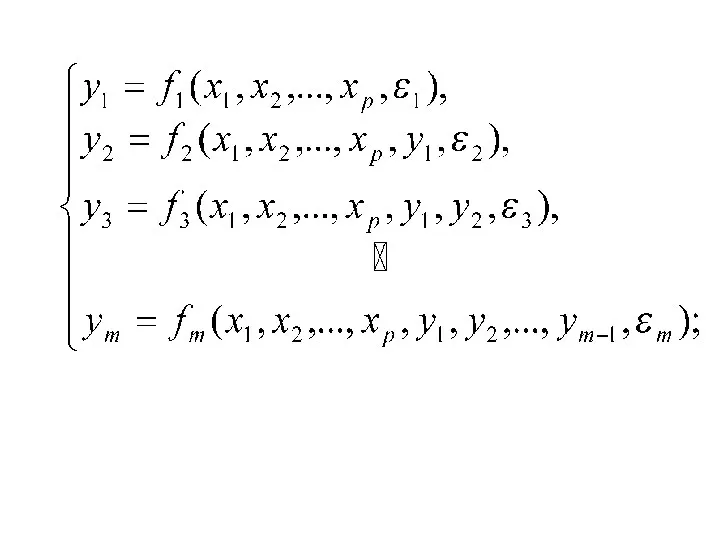


































 Возведение в степень произведения и степени
Возведение в степень произведения и степени Свойства функции y=cos-x и ее график
Свойства функции y=cos-x и ее график Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3
Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3 Закрепление + - 3. Сравнение отрезков. 1 класс Школа России
Закрепление + - 3. Сравнение отрезков. 1 класс Школа России Степени и корни. Свойства степеней
Степени и корни. Свойства степеней Софья Ковалевская
Софья Ковалевская Числа 1 - 4
Числа 1 - 4 Метрология. Введение. Структура дисциплины
Метрология. Введение. Структура дисциплины grafy1
grafy1 Число и цифра 4.
Число и цифра 4. Тренажёр умножения на 2
Тренажёр умножения на 2 Статистическое распределение выборки и его основные числовые характеристики
Статистическое распределение выборки и его основные числовые характеристики Раскрытие скобок
Раскрытие скобок Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9 Урок математики для 2 класса Трёхзначные числа
Урок математики для 2 класса Трёхзначные числа НОД по математическому развитию в подготовительной группе.
НОД по математическому развитию в подготовительной группе. Решение обыкновенных дифференциальных уравнений (краевая задача)
Решение обыкновенных дифференциальных уравнений (краевая задача) Раскрытие скобок
Раскрытие скобок Цікаві факти з історії геометрії
Цікаві факти з історії геометрії Grafika komputerowa
Grafika komputerowa Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Формула пути. Решение задач на движение
Формула пути. Решение задач на движение Тест по теме: Тетраэдр и параллелепипед. Теория
Тест по теме: Тетраэдр и параллелепипед. Теория Система подготовки к ЕГЭ
Система подготовки к ЕГЭ Марковские системы массового обслуживания
Марковские системы массового обслуживания Логарифмы вокруг нас. История логарифмов
Логарифмы вокруг нас. История логарифмов Три точки зрения на геометрию вселенной
Три точки зрения на геометрию вселенной Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс
Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс