Содержание
- 2. Пусть - матрица, - вектор, - число. Рассмотрим уравнение называется собственным значением, - собственным вектором. Такое
- 3. Например, если то т.е. длина вектора увеличивается в 2 раза. Если же то длина вектора уменьшается
- 4. Рассмотрим Запишем матричное уравнение в координатной форме.
- 5. Преобразуем
- 6. Получилась система линейных однородных уравнений. Такая система всегда имеет нулевое решение. Нас интересует случай, когда система
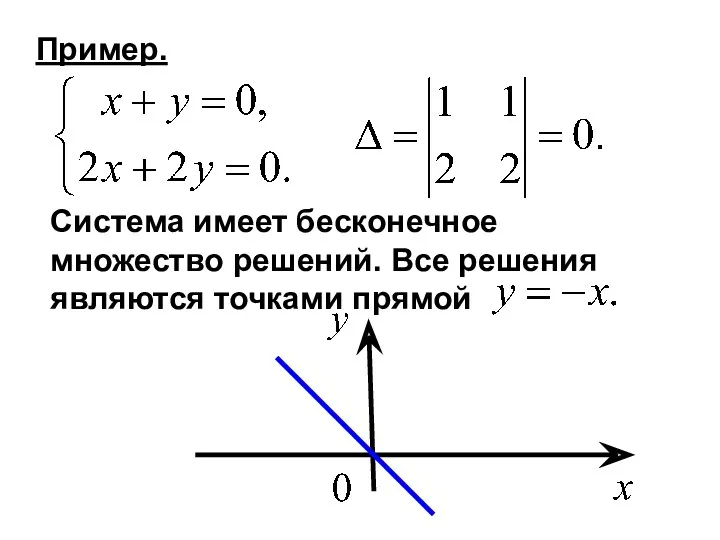
- 7. Пример. Система имеет бесконечное множество решений. Все решения являются точками прямой
- 8. Вернемся к нашей системе. Составим определитель системы или Получилось квадратное уравнение. Такое уравнение называется характеристическим. Корни
- 9. Примеры. 1. Найти собственные значения матрицы Запишем матрицу
- 10. Находим корни характеристического уравнения или Мы нашли собственные значения. Ответ:
- 11. Нахождение собственных векторов 1. Найдем собственный вектор, соответствующий собственному значению Рассмотрим уравнение и вместо подставим
- 12. Тогда получим или
- 13. Отсюда Положим тогда Получилось
- 14. Можно считать, что мы нашли собственный вектор. Но обычно этот вектор нормируют, т.е. приводят его к
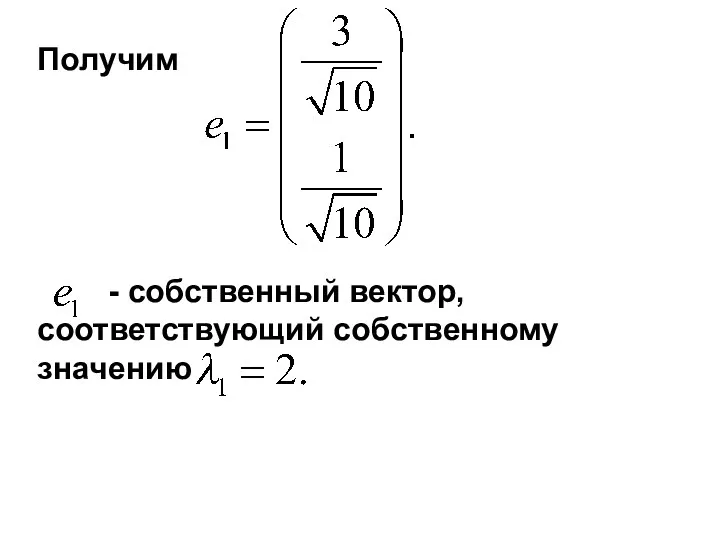
- 15. Получим - собственный вектор, соответствующий собственному значению
- 16. Аналогично найдем т.е. собственный вектор, соответствующий
- 17. Пусть тогда Нормируем, т.е. разделим на Получим
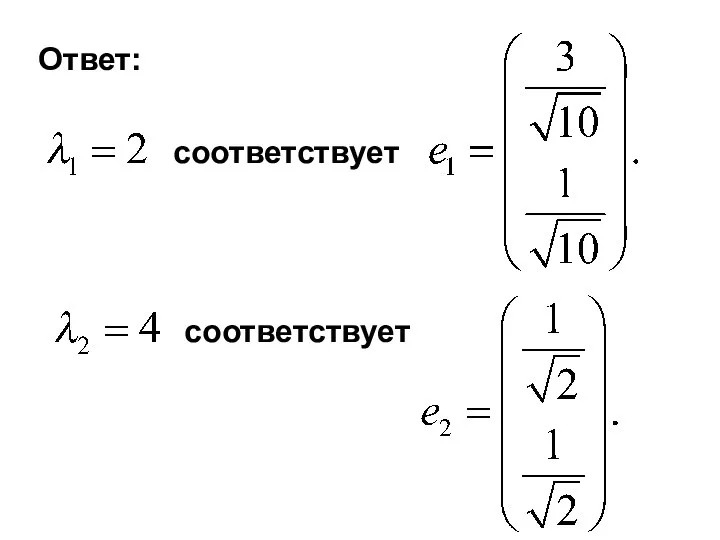
- 18. Ответ: соответствует соответствует
- 19. Функция. Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции и
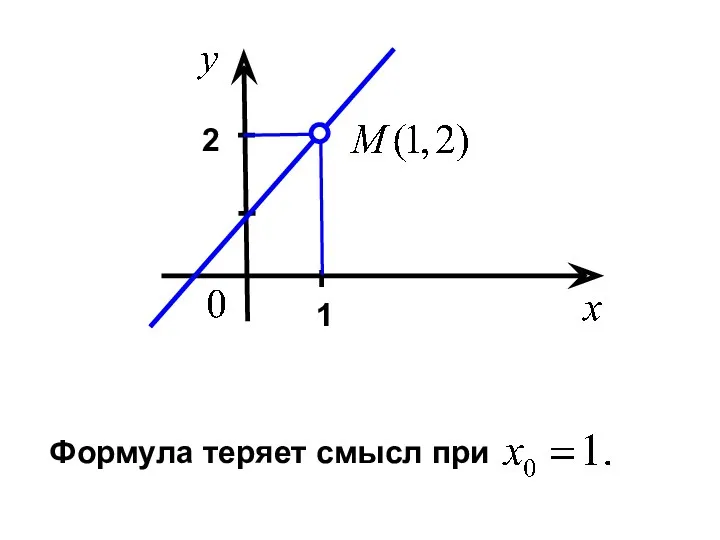
- 20. 1. Предел в точке. Рассмотрим пример. Построить график функции
- 21. 1 2
- 22. В этом случае пишут: По-другому: при
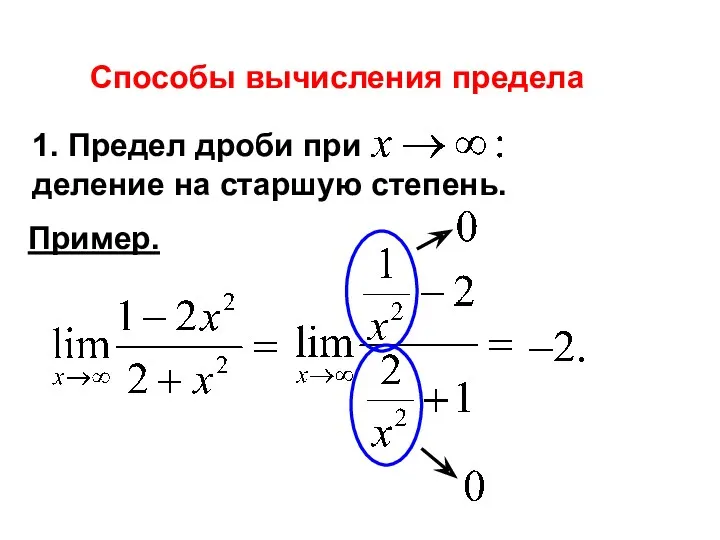
- 23. Способы вычисления предела 1. Предел дроби при деление на старшую степень. Пример.
- 24. 2. Разложение на множители, когда Пример.
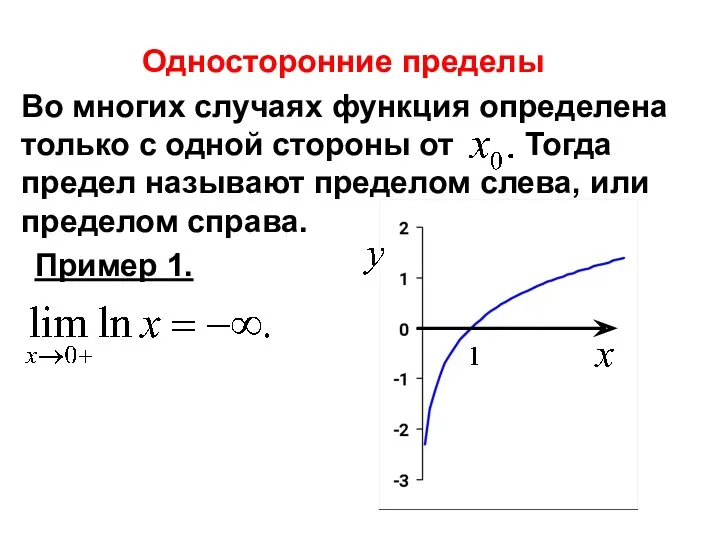
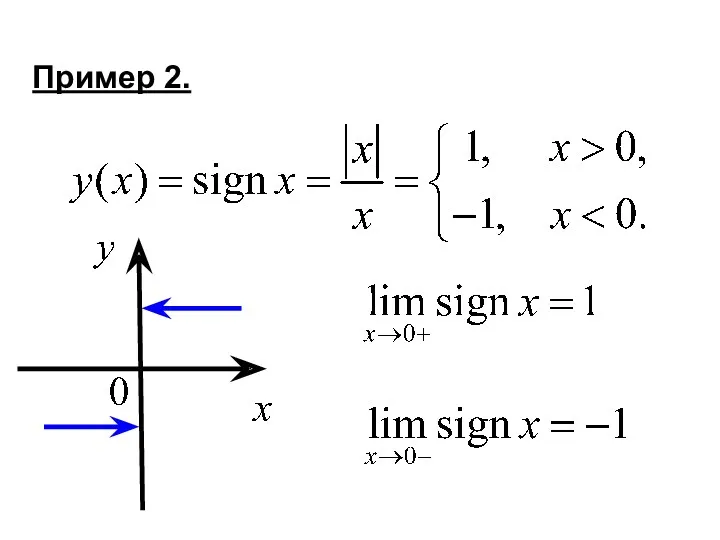
- 25. Односторонние пределы Пример 1.
- 26. Пример 2.
- 27. Опр. Функция называется непрерывной в точке если Все элементарные функции непрерывны на своей области определения. Пример.
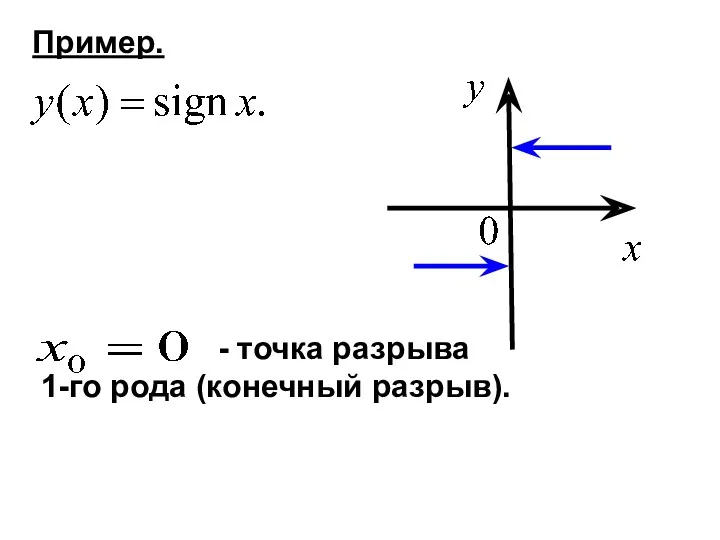
- 28. Опр. Если в точке функция не является непрерывной, то - точка разрыва. Рассматриваются точки разрыва 1-го
- 29. Пример. - точка разрыва 1-го рода (конечный разрыв).
- 31. Скачать презентацию



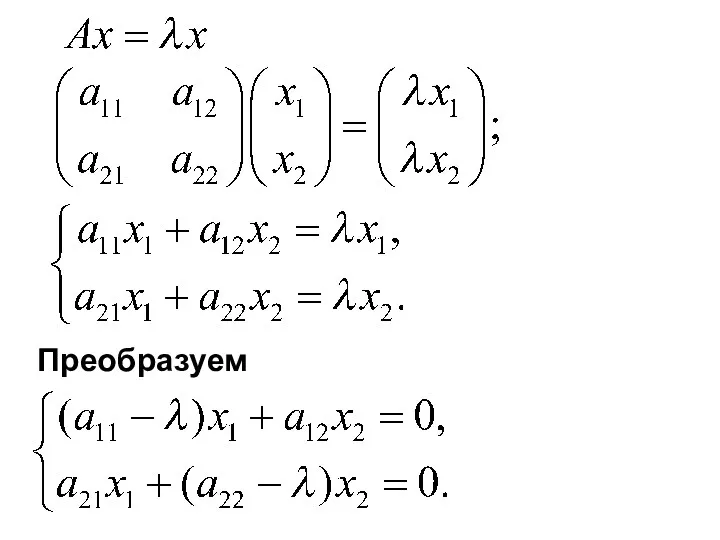





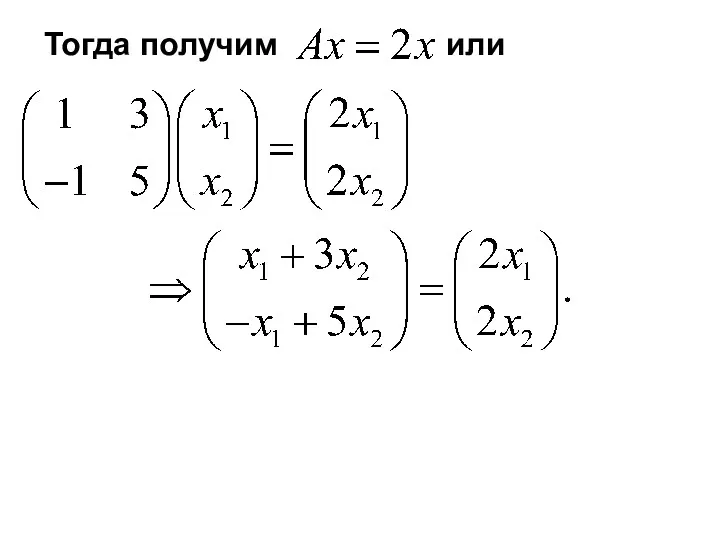










 Задачи на вероятность
Задачи на вероятность Составление задач на сложение и вычитание по одному рисунку
Составление задач на сложение и вычитание по одному рисунку Логические задачи-шутки на уроках математики в первом классе
Логические задачи-шутки на уроках математики в первом классе Основные определения реляционной модели данных
Основные определения реляционной модели данных Числа от 11 до 20. Нумерация
Числа от 11 до 20. Нумерация Линейные уравнения с одной переменной
Линейные уравнения с одной переменной Реши ребус – отгадай слово
Реши ребус – отгадай слово КВН урок математики в 3 классе
КВН урок математики в 3 классе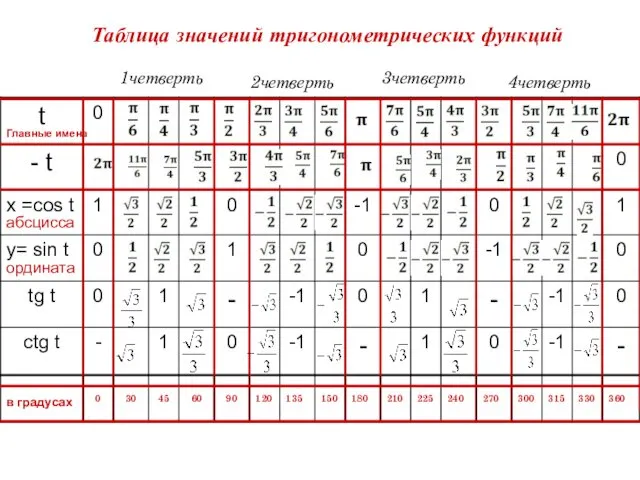 Таблица значений тригонометрических функций
Таблица значений тригонометрических функций Аксиомы параллельных прямых
Аксиомы параллельных прямых Виды треугольников
Виды треугольников Транспортная задача. (Лекции 10,11)
Транспортная задача. (Лекции 10,11) Моделирование индивидуальной траектории развития одаренных детей по математике в 5-9 классах
Моделирование индивидуальной траектории развития одаренных детей по математике в 5-9 классах Решение уравнений, сводящихся к квадратным
Решение уравнений, сводящихся к квадратным Среднее арифметическое, размах и мода. Алгебра. 8 класс
Среднее арифметическое, размах и мода. Алгебра. 8 класс Анализ систем методами теории массового обслуживания
Анализ систем методами теории массового обслуживания Вписанные и описанные окружности. Задания для устного счета. Упражнение 14. 8 класс
Вписанные и описанные окружности. Задания для устного счета. Упражнение 14. 8 класс Презентация к уроку математики. Л.Г. Петерсон Умножение и деление на 10, 100 (продолжение)
Презентация к уроку математики. Л.Г. Петерсон Умножение и деление на 10, 100 (продолжение) Игра Кто хочет стать математиком
Игра Кто хочет стать математиком Математический аукцион
Математический аукцион Презентация к уроку по теме Теорема Пифагора
Презентация к уроку по теме Теорема Пифагора Оценивание спектральной плотности мощности
Оценивание спектральной плотности мощности Конспект занятия с презентацией по ФЭМП в средней группе по теме Учимся с Лунтиком!
Конспект занятия с презентацией по ФЭМП в средней группе по теме Учимся с Лунтиком! проектная задача Доктор Айболит
проектная задача Доктор Айболит Обыкновенные дроби. Сокращение дробей
Обыкновенные дроби. Сокращение дробей Измерительные работы на местности. Творческое название: Геометрия на свежем воздухе
Измерительные работы на местности. Творческое название: Геометрия на свежем воздухе Вероятность и статистика. 9 класс. Урок № 1
Вероятность и статистика. 9 класс. Урок № 1 Практикум по решению стереометрических задач
Практикум по решению стереометрических задач