- Главная
- Математика
- Средняя линия трапеции (несколько способов доказательства)

Содержание
- 2. Объект исследования: трапеция, средняя линия трапеции. Цель: показать, что доказательство теоремы о средней линии трапеции с
- 3. А можно ли доказать? Теорема – математическое утверждение, истинность которого установлена путем доказательства [3]. Классическая теорема
- 4. Теоретическая часть Средней линией треугольника называется отрезок, соединяющей середины двух его сторон. Средней линией трапеции называется
- 5. Следствие 2° из аксиомы параллельных. Если две прямые параллельны третьей прямой, то они параллельны. Теорема о
- 6. Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство № 1. Доказательство. 1. Для
- 7. Доказательство. 1. Для доказательства возьмём на основании AD точку Е. Из точки Е через точки М
- 8. Доказательство. 1. На основании BC возьмём произвольную точку Е. Из точки Е через точки М и
- 9. Доказательство. 1. Для доказательства на продолжении основания АD откладываем отрезок DE=BC. Точку В соединяем с точкой
- 10. Доказательство. 1. Для доказательства на продолжении основания ВС отложим A1C=AD, а на AD отложим B1D=BC.Соединим точку
- 11. Доказательство продолжение. 3. Рассмотрим четырёхугольник ABA1В1. BA1= AВ1 (по построению); BA1 || AВ1 (так как BC
- 12. Доказательство. 1. Для доказательства на продолжении основания AD отложим отрезок DE=BC. А также на продолжении средней
- 13. Доказательство. 1. Для доказательства через точку N проведём прямую EK || AB до пересечения этой прямой
- 14. Доказательство продолжение. 4. Рассмотрим четырёхугольники MBEN и AMNK. MB = EN и MB|| EN. Значит по
- 15. Заключение Поставленная цель достигнута. Теорема о средней линии трапеции доказана семью способами с помощью признаков равенства
- 16. Литература Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов средней школы». М.: Издательство «Просвещение» 2010 г.
- 18. Скачать презентацию
Объект исследования: трапеция, средняя линия трапеции.
Цель: показать, что доказательство теоремы о
Объект исследования: трапеция, средняя линия трапеции.
Цель: показать, что доказательство теоремы о
Задачи:
Изучение научной и учебной литературы по заданной теме.
Привести другие способы доказательства теоремы о средней линии трапеции.
При доказательстве этой теоремы показать значение других теорем: признаков равенства треугольников, теоремы о параллельности прямых, теоремы о средней линии треугольника, а также следствие из аксиомы параллельных прямых, и определение средней линии треугольника и средней линии трапеции, признаки и определение параллелограмма.
Методы исследования: применение аналитического и синтетического методов доказательства теорем.
А можно ли доказать?
Теорема – математическое утверждение, истинность которого установлена путем
А можно ли доказать?
Теорема – математическое утверждение, истинность которого установлена путем
Классическая теорема состоит из двух частей: из условия и заключения. Условие обыкновенно начинается со слова «если», а заключение со слова «то».
Исходная теорема называется прямой теоремой
Обратная теорема - если в исходной теореме условие сделать заключением, а заключение – условием.
Если верна прямая теорема, то обратная теорема может быть неверной
Взаимно обратные теоремы - если верны прямая и обратная теоремы
Доказательством называется конечная последовательность формул, каждая из которых либо является аксиомой, либо получается из некоторых предыдущих формул этой последовательности по одному из правил вывода [3].
Теоретическая часть
Средней линией треугольника называется отрезок, соединяющей середины двух его сторон.
Средней
Теоретическая часть
Средней линией треугольника называется отрезок, соединяющей середины двух его сторон.
Средней
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Два угла называются вертикальными, если стороны одного угла являются продолжением сторон другого. вертикальные.
Прямые a и b параллельны, с –секущая.
Пары углов:
называются накрест лежащими.
Свойство вертикальных углов. Вертикальные углы равны
Следствие 2° из аксиомы параллельных. Если две прямые параллельны третьей прямой,
Следствие 2° из аксиомы параллельных. Если две прямые параллельны третьей прямой,
Теорема о средней линии треугольника. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Второй признак равенства треугольников. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Признак параллельности двух прямых. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Признак параллелограмма 1°. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство
Теорема: Средняя линия трапеции параллельна основаниям и равна их полусумме. Доказательство
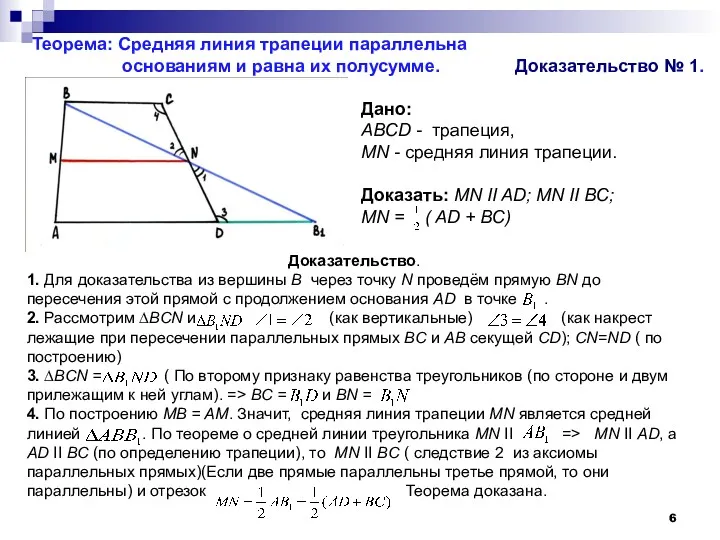
Доказательство.
1. Для доказательства из вершины B через точку N проведём прямую BN до пересечения этой прямой с продолжением основания AD в точке .
2. Рассмотрим ∆BCN и (как вертикальные) (как накрест лежащие при пересечении параллельных прямых BC и АB секущей CD); CN=ND ( по построению)
3. ∆BCN = ( По второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам). => BC = и BN = .
4. По построению MB = AM. Значит, средняя линия трапеции MN является средней линией . По теореме о средней линии треугольника MN II => MN II AD, а AD II BC (по определению трапеции), то MN II BC ( следствие 2 из аксиомы параллельных прямых)(Если две прямые параллельны третье прямой, то они параллельны) и отрезок Теорема доказана.
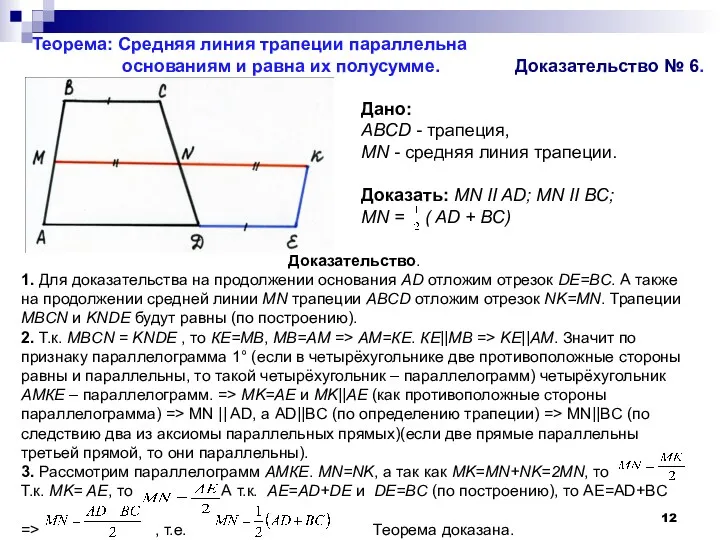
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
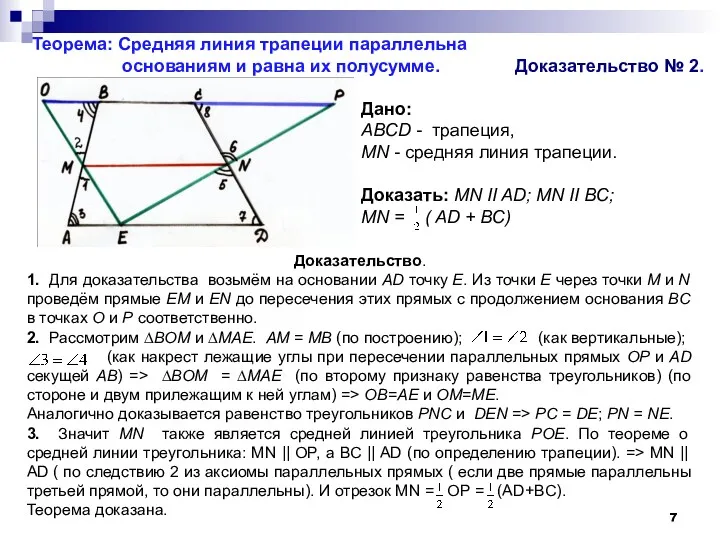
Доказательство.
1. Для доказательства возьмём на основании AD точку Е. Из точки
Доказательство.
1. Для доказательства возьмём на основании AD точку Е. Из точки
2. Рассмотрим ∆BOM и ∆MAE. AM = MB (по построению); (как вертикальные);
(как накрест лежащие углы при пересечении параллельных прямых OP и AD секущей АВ) => ∆BOM = ∆MAE (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам) => OB=AE и OM=ME.
Аналогично доказывается равенство треугольников PNC и DEN => PC = DE; PN = NE.
3. Значит MN также является средней линией треугольника POE. По теореме о средней линии треугольника: MN || OP, а BC || AD (по определению трапеции). => MN || AD ( по следствию 2 из аксиомы параллельных прямых ( если две прямые параллельны третьей прямой, то они параллельны). И отрезок MN = OP = (AD+BC).
Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 2.
Доказательство.
1. На основании BC возьмём произвольную точку Е. Из точки Е
Доказательство.
1. На основании BC возьмём произвольную точку Е. Из точки Е
2. Рассмотрим ∆МВЕ и ∆АОМ. (как вертикальные); (как накрест лежащие углы при пересечении параллельных прямых ВС и ОР секущей АВ); АМ=МВ (по построению). => ∆МВЕ =∆АОМ (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам) => ВЕ=ОА и ЕМ = ОМ. Аналогично доказывается равенство треугольников СЕN и PND => EN=NP и EC=PD.
3. Значит MN также является средней линией треугольника POE. По теореме о средней линии треугольника MN || OP => MN || AD, а AD || BC (по определению трапеции) => MN || BC (по следствию 2 из аксиомы параллельных прямых (если две прямые параллельны третьей прямой, то они параллельны) и отрезок
Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 3.
Доказательство.
1. Для доказательства на продолжении основания АD откладываем отрезок DE=BC. Точку
Доказательство.
1. Для доказательства на продолжении основания АD откладываем отрезок DE=BC. Точку
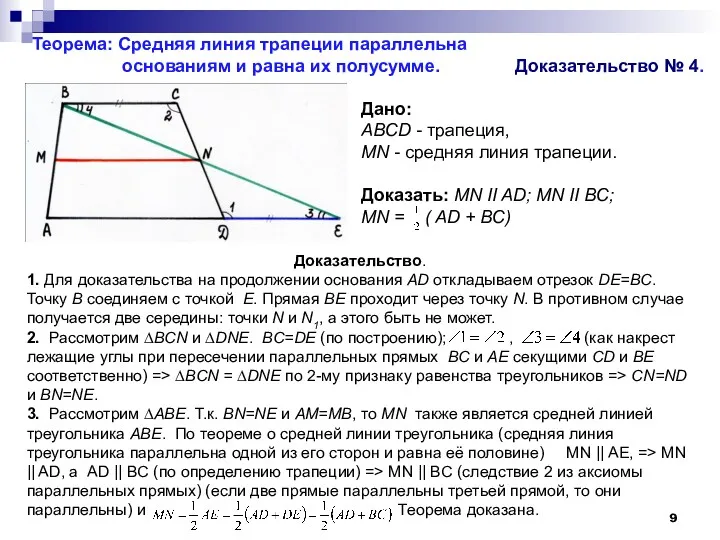
2. Рассмотрим ∆BCN и ∆DNE. BC=DE (по построению); , (как накрест лежащие углы при пересечении параллельных прямых ВС и АЕ секущими СD и ВЕ соответственно) => ∆BCN = ∆DNE по 2-му признаку равенства треугольников => CN=ND и BN=NE.
3. Рассмотрим ∆АВЕ. Т.к. BN=NE и АМ=МВ, то MN также является средней линией треугольника АВЕ. По теореме о средней линии треугольника (средняя линия треугольника параллельна одной из его сторон и равна её половине) MN || AE, => MN || AD, а AD || BC (по определению трапеции) => MN || BC (следствие 2 из аксиомы параллельных прямых) (если две прямые параллельны третьей прямой, то они параллельны) и Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 4.
Доказательство.
1. Для доказательства на продолжении основания ВС отложим A1C=AD, а на
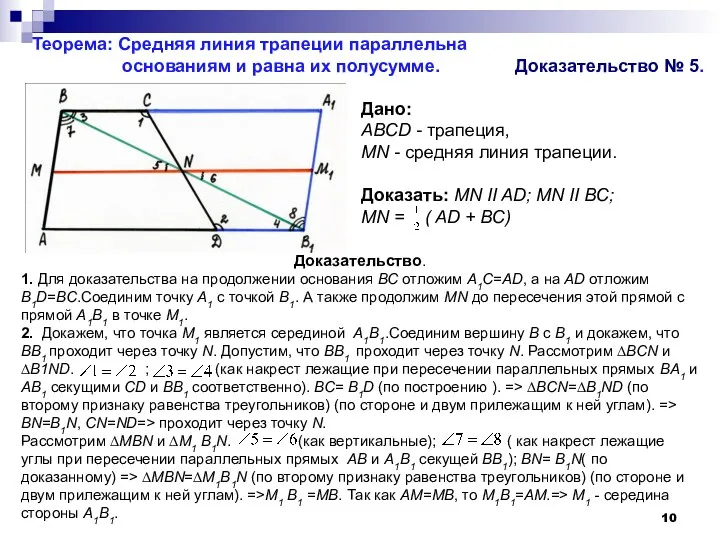
Доказательство.
1. Для доказательства на продолжении основания ВС отложим A1C=AD, а на
2. Докажем, что точка M1 является серединой A1В1.Соединим вершину В с В1 и докажем, что BВ1 проходит через точку N. Допустим, что BВ1 проходит через точку N. Рассмотрим ∆ВСN и ∆B1ND. ; (как накрест лежащие при пересечении параллельных прямых BA1 и АВ1 секущими CD и ВВ1 соответственно). ВС= B1D (по построению ). => ∆BCN=∆B1ND (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). => BN=B1N, CN=ND=> проходит через точку N.
Рассмотрим ∆MBN и ∆M1 B1N. (как вертикальные); ( как накрест лежащие углы при пересечении параллельных прямых АВ и А1В1 секущей ВВ1); BN= В1N( по доказанному) => ∆MBN=∆M1В1N (по второму признаку равенства треугольников) (по стороне и двум прилежащим к ней углам). =>M1 В1 =MB. Так как AM=MB, то M1В1=AM.=> M1 - середина стороны A1В1.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 5.
Доказательство продолжение.
3. Рассмотрим четырёхугольник ABA1В1. BA1= AВ1 (по построению); BA1 ||
Доказательство продолжение.
3. Рассмотрим четырёхугольник ABA1В1. BA1= AВ1 (по построению); BA1 ||
построению. Значит MN=M1N =>
4. По построению AB || A1В1 => AM || B1M1 и MB || A1M1. Т.к. трапеции ABCD и A1В1DC равны, то => MB=M1B1 и AM=A1M1,а так как АМ=МВ и А1М1= M1B1 (по построению), то АМ=МВ= A1M1=M1B1. Значит четырёхугольники МВA1M1 и АМM1B1 – параллелограммы (по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник – параллелограмм).=> BА1||MM1 и BА1=MM1; MM1=AВ1 и MM1 || AВ1 ( как противоположные стороны параллелограмма). =>MN || BC; BC||AD => MN || AD( по следствию два из аксиомы параллельных прямых (если две прямые параллельны третье прямой, то они параллельны).
5. Т.к. BA1=MM1, то т.е. А т.к. BA1=ВС+СA1, а CA1 =AD (по построению), то
BA1=ВС+AD. Значит Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 5.
Доказательство.
1. Для доказательства на продолжении основания AD отложим отрезок DE=BC. А
Доказательство.
1. Для доказательства на продолжении основания AD отложим отрезок DE=BC. А
2. Т.к. MBCN = KNDE , то КЕ=МВ, МВ=АМ => АМ=КЕ. КЕ||MB => KE||AM. Значит по признаку параллелограмма 1° (если в четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник – параллелограмм) четырёхугольник АМКЕ – параллелограмм. => MK=AE и MK||AE (как противоположные стороны параллелограмма) => MN || AD, а AD||BC (по определению трапеции) => MN||BC (по следствию два из аксиомы параллельных прямых)(если две прямые параллельны третьей прямой, то они параллельны).
3. Рассмотрим параллелограмм АМКЕ. MN=NK, а так как MK=MN+NK=2MN, то Т.к. MK= AE, то А т.к. AE=AD+DE и DE=BC (по построению), то AE=AD+BC
=> , т.е. Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 6.
Доказательство.
1. Для доказательства через точку N проведём прямую EK || AB
Доказательство.
1. Для доказательства через точку N проведём прямую EK || AB
2. Рассмотрим ∆NEC и ∆NKD; CN=ND (по построению), (как вертикальные);
(как накрест лежащие углы при пересечении параллельных прямых BE и AD секущей CD). =>∆NEC=∆NKD (по второму признаку равенства треугольников( по стороне и двум прилежащим к ней углам). => CE=KD и EN=NK.
3. Рассмотрим четырёхугольник ABEK. AB || EK (по построению), BC || AD , => BE||AD (по определению трапеции) => четырёхугольник АВЕК – параллелограмм (по определению параллелограмма).=> AB=EK и AB || EK (как противоположные стороны параллелограмма). И EN=NK (из равенства треугольников NEC и NKD (по второму признаку равенства треугольников (по стороне и двум прилежащим к ней углам), а AM=MB (по построению).
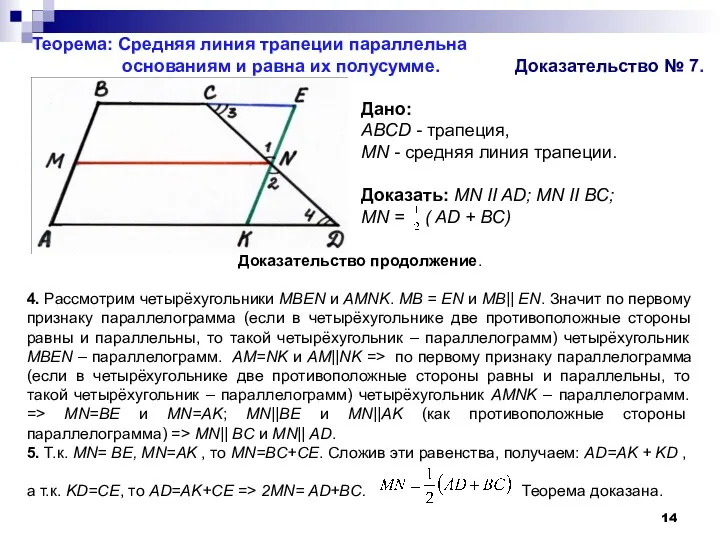
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 7.
Доказательство продолжение.
4. Рассмотрим четырёхугольники MBEN и AMNK. MB = EN и
Доказательство продолжение.
4. Рассмотрим четырёхугольники MBEN и AMNK. MB = EN и
5. Т.к. MN= BE, MN=AK , то MN=BC+CE. Сложив эти равенства, получаем: AD=AK + KD ,
а т.к. KD=CE, то AD=AK+CE => 2MN= AD+BC. Теорема доказана.
Дано:
ABCD - трапеция,
MN - средняя линия трапеции.
Доказать: МN II AD; MN II BC;
MN = ( AD + BС)
Теорема: Средняя линия трапеции параллельна
основаниям и равна их полусумме. Доказательство № 7.
Заключение
Поставленная цель достигнута. Теорема о средней линии трапеции доказана семью
Заключение
Поставленная цель достигнута. Теорема о средней линии трапеции доказана семью
Литература
Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов средней школы». М.:
Литература
Атанасян Л.С. «Геометрия 7-9. Учебник для 7-9 классов средней школы». М.:
Далингер В.А. «Методика работы над формулировкой и доказательством и закреплением теоремы». Омск. Издательство «ОмИПКРО» 1995 г.
Математическая энциклопедия под редакцией И.М. Виноградова. М.: Изд. Советская Энциклопедия, 1984 г, том 4 и том 5.
Погорелов А.В. «Геометрия 7-11. Учебник для 7-11 классов средней школы». М.: Издательство «Просвещение» 2010 г.
Энциклопедия для детей. Том 11. Математика/ Глав. ред. М.Д. Аксенова. – М.: Аванта+, 2000 г.
Якушева Г.М. «Математика. Справочник школьника». М.: Издательство «Слово» 1995 г.
Якушева Г.М. «Решение задач по математике. Справочник школьника». М.: Издательство «Слово». 1996 г.









 Урок математики в 1 классе по теме Числа от 0 до 20
Урок математики в 1 классе по теме Числа от 0 до 20 Решение задач на готовых чертежах. Подобные треугольники
Решение задач на готовых чертежах. Подобные треугольники Точечные и интервальные оценки неизвестных параметров распределения
Точечные и интервальные оценки неизвестных параметров распределения Алгебра логики. Основные понятия
Алгебра логики. Основные понятия Использование ИКТ на уроках математики
Использование ИКТ на уроках математики Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника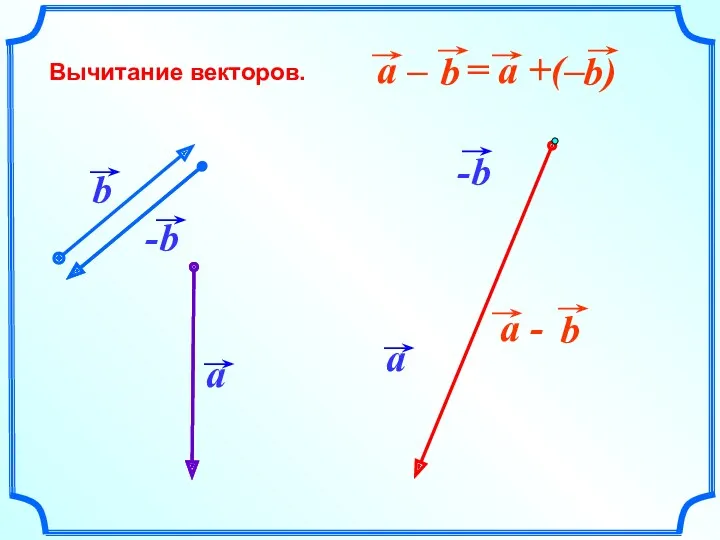 Вычитание и сложение векторов. Правило параллелограмма
Вычитание и сложение векторов. Правило параллелограмма Формулы сокращённого умножения
Формулы сокращённого умножения Что есть Время? Иудейский календарь Исламский календарь
Что есть Время? Иудейский календарь Исламский календарь Параллельный перенос
Параллельный перенос Решение задач с параметром, графическим способом
Решение задач с параметром, графическим способом Задачи повышенной сложности.
Задачи повышенной сложности. Приёмы табличного вычитания однозначных чисел с переходом через десяток
Приёмы табличного вычитания однозначных чисел с переходом через десяток Примеры на вычитание с переходом через десяток в пределах 20. 1 класс
Примеры на вычитание с переходом через десяток в пределах 20. 1 класс Каталог авторских дидактических материалов по интерактивному оборудованию
Каталог авторских дидактических материалов по интерактивному оборудованию презентация по математике
презентация по математике Использование современных технологий на уроках математики
Использование современных технологий на уроках математики Умножение и деление на 10, 100
Умножение и деление на 10, 100 Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Презентация к уроку математики по теме Сложение 1 класс
Презентация к уроку математики по теме Сложение 1 класс Квадратные уравнения
Квадратные уравнения Лекция 10. Математическое описание ЛС. Линейная непрерывная система и ее представления
Лекция 10. Математическое описание ЛС. Линейная непрерывная система и ее представления Состав числа 5 из двух слагаемых
Состав числа 5 из двух слагаемых Пословицы в диаграммах: занимательно о русском языке
Пословицы в диаграммах: занимательно о русском языке Мера центральной тенденции. Средние величины и изучение вариации
Мера центральной тенденции. Средние величины и изучение вариации Устный счёт. Думай, считай, отвечай
Устный счёт. Думай, считай, отвечай Что наша жизнь? – игра… Проект-исследование
Что наша жизнь? – игра… Проект-исследование Тригонометрические уравнения
Тригонометрические уравнения