Содержание
- 2. TPMN 2019/2020 : Solving the Schr¨odinger equation e M. Alouani, mebarek.alouani@ipcms.unistra.fr, IPCMS e H. Bulou, herve.bulou@ipcms.unistra.fr,
- 3. TPMN 2019/2020 : Solving the Schr¨odinger equation e M. Alouani, mebarek.alouani@ipcms.unistra.fr, IPCMS e H. Bulou, herve.bulou@ipcms.unistra.fr,
- 4. TPMN 2019/2020 : Solving the Schr¨odinger equation e M. Alouani, mebarek.alouani@ipcms.unistra.fr, IPCMS e H. Bulou, herve.bulou@ipcms.unistra.fr,
- 5. TPMN 2019/2020 : Solving the Schr¨odinger equation e M. Alouani, mebarek.alouani@ipcms.unistra.fr, IPCMS e H. Bulou, herve.bulou@ipcms.unistra.fr,
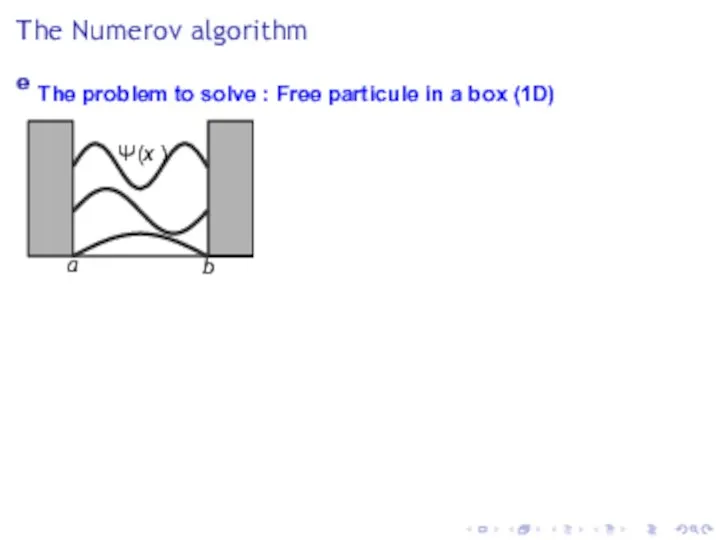
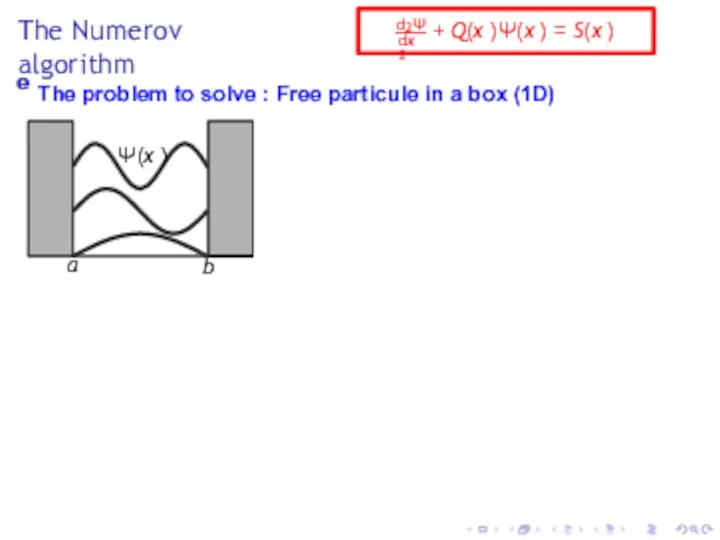
- 6. The Numerov algorithm e The problem to solve : Free particule in a box (1D) Ψ(x
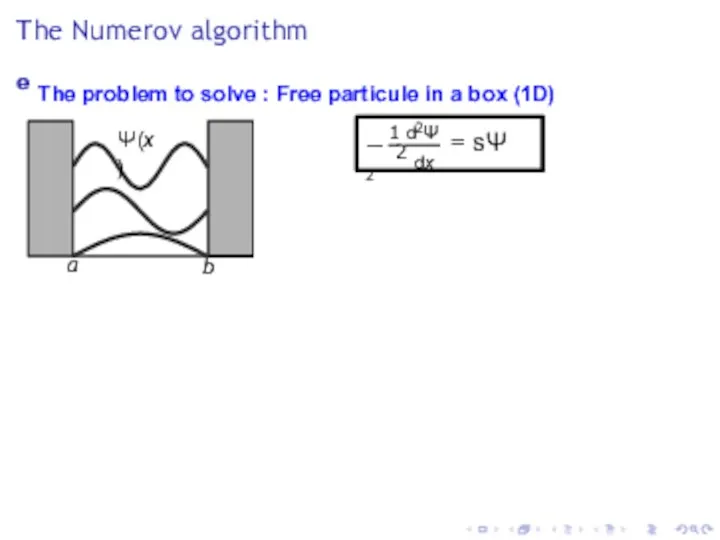
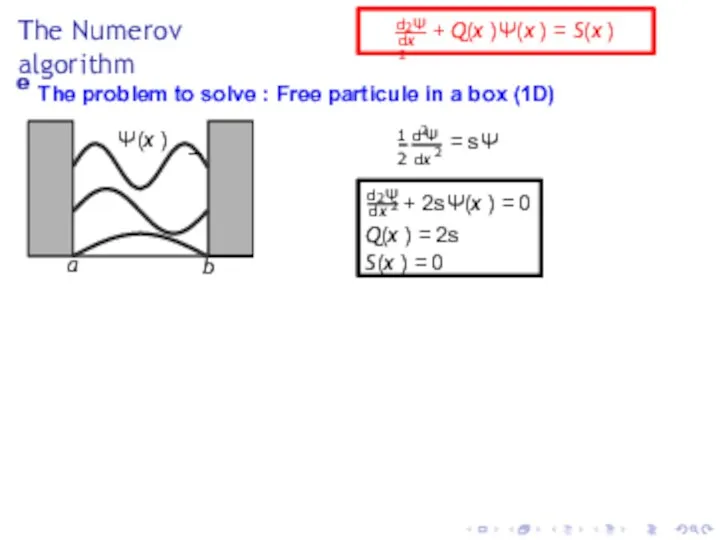
- 7. The Numerov algorithm e The problem to solve : Free particule in a box (1D) Ψ(x
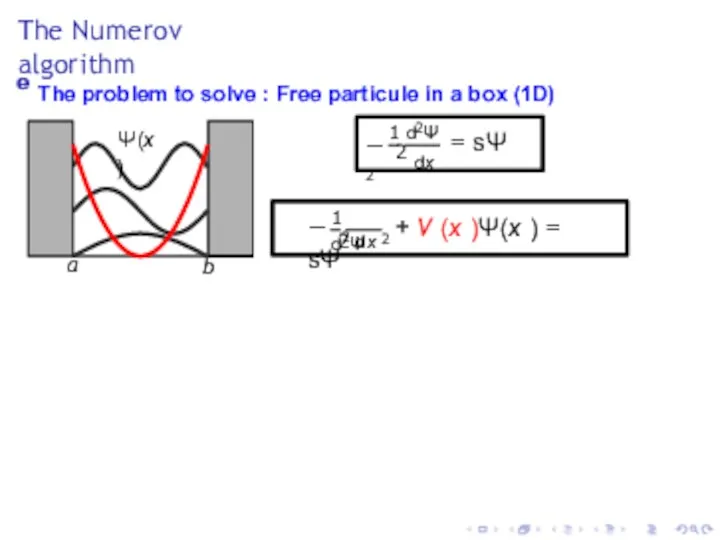
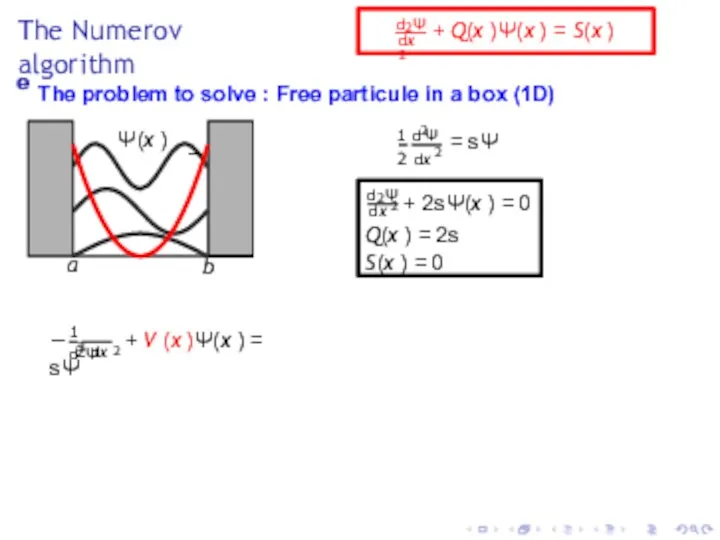
- 8. The Numerov algorithm e The problem to solve : Free particule in a box (1D) Ψ(x
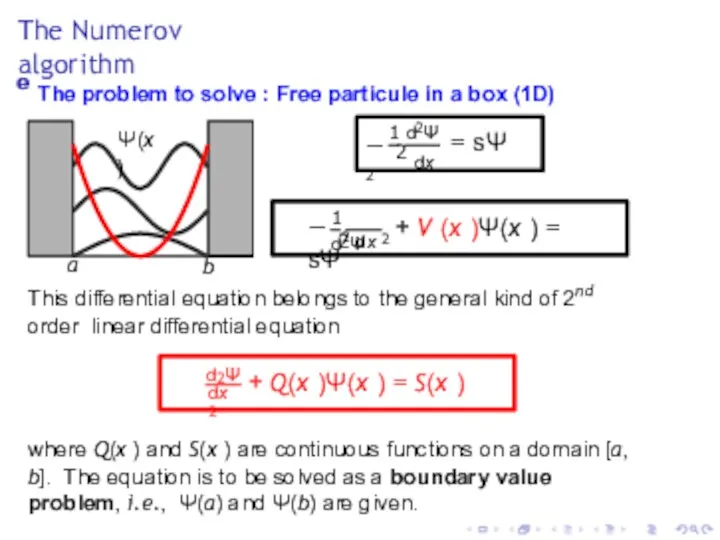
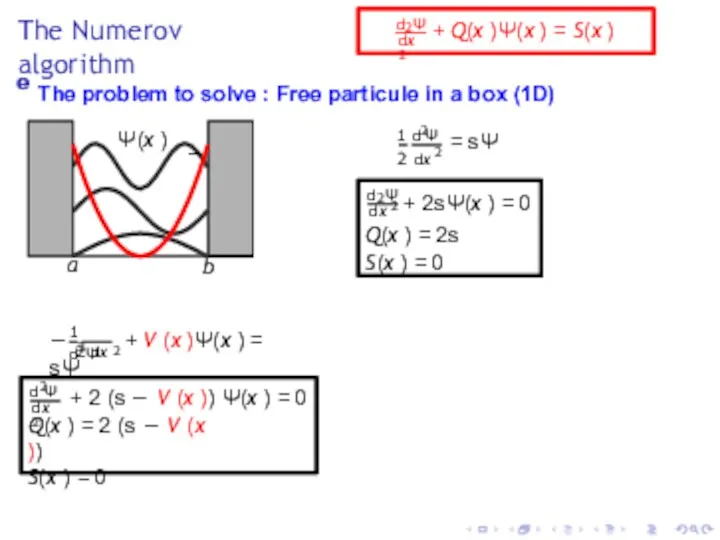
- 9. The Numerov algorithm e The problem to solve : Free particule in a box (1D) Ψ(x
- 10. The Numerov algorithm dx 2 d2Ψ + Q(x )Ψ(x ) = S(x ) 2 − ∇
- 11. The Numerov algorithm dx 2 d2Ψ + Q(x )Ψ(x ) = S(x ) Depending of the
- 12. The Numerov algorithm e The problem to solve : Free particule in a box (1D) Ψ(x
- 13. The Numerov algorithm e The problem to solve : Free particule in a box (1D) a
- 14. The Numerov algorithm e The problem to solve : Free particule in a box (1D) a
- 15. The Numerov algorithm e The problem to solve : Free particule in a box (1D) a
- 16. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆,
- 17. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆, e
- 18. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆, e
- 19. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆, e
- 20. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆, e
- 21. The Numerov algorithm Ψ(x ) a b ∆ e We consider a grid, step ∆, e
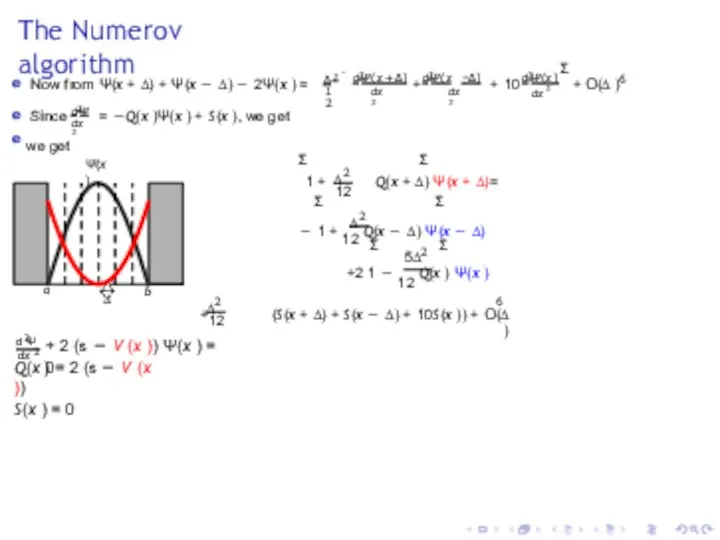
- 22. The Numerov algorithm Ψ(x ) a b ∆ Now from Ψ(x + ∆) + Ψ(x −
- 23. The Numerov algorithm Ψ(x ) a b ∆ Σ ∆2 12 Σ 1 + Q(x +
- 24. The Numerov algorithm Ψ(x ) a b ∆ Σ ∆2 12 Σ 1 + Q(x +
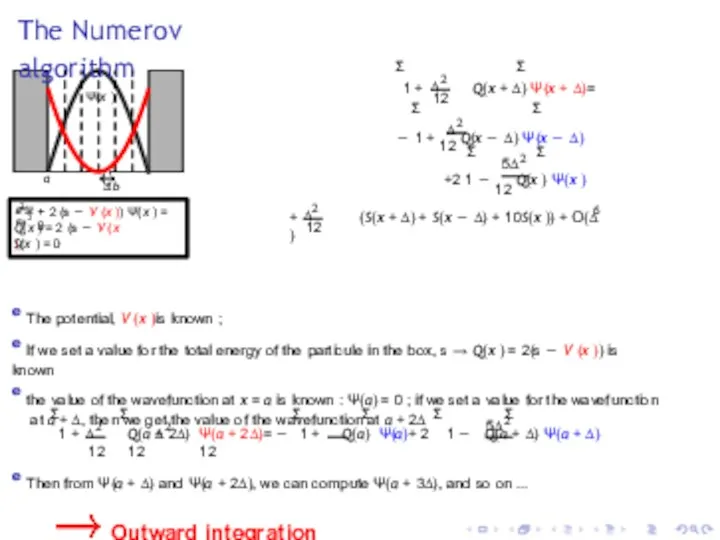
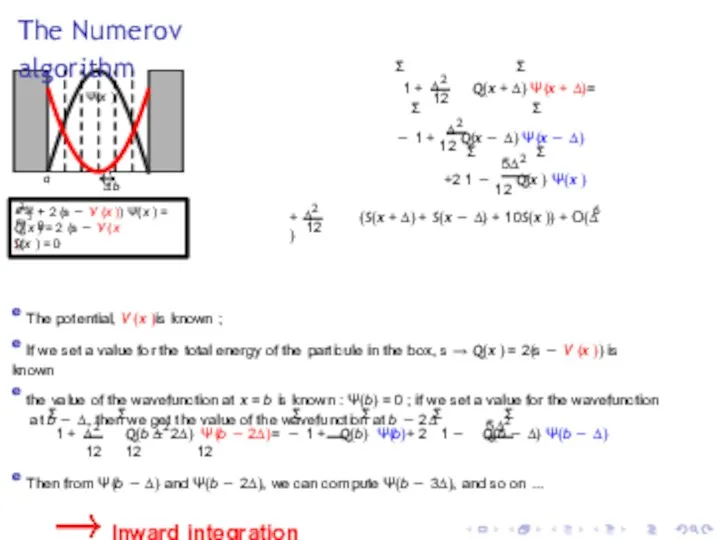
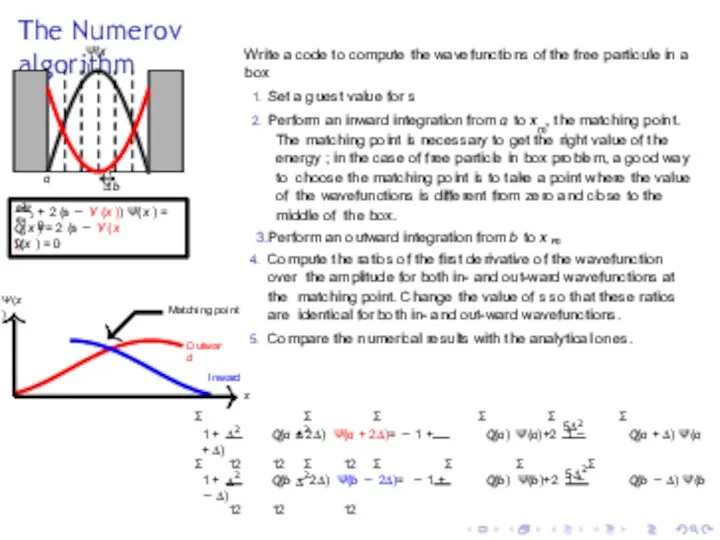
- 25. The Numerov algorithm Ψ(x ) a b ∆ 2 d Ψ dx 2 + 2 (s
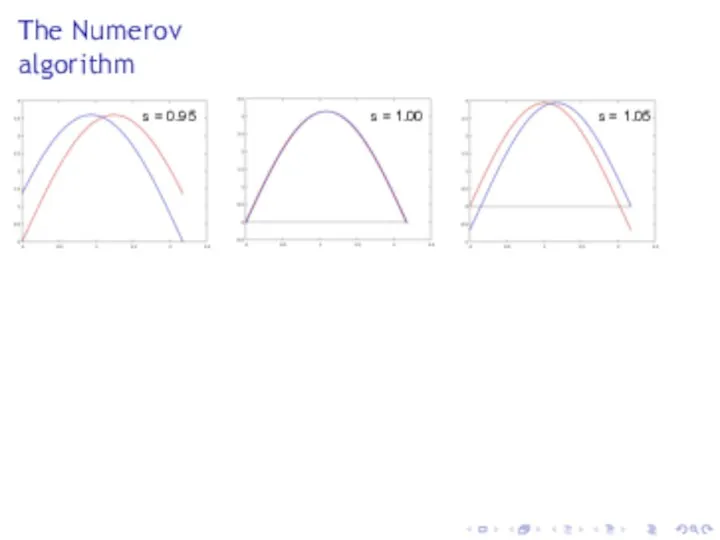
- 26. The Numerov algorithm s = 0.95 s = 1.00 s = 1.05
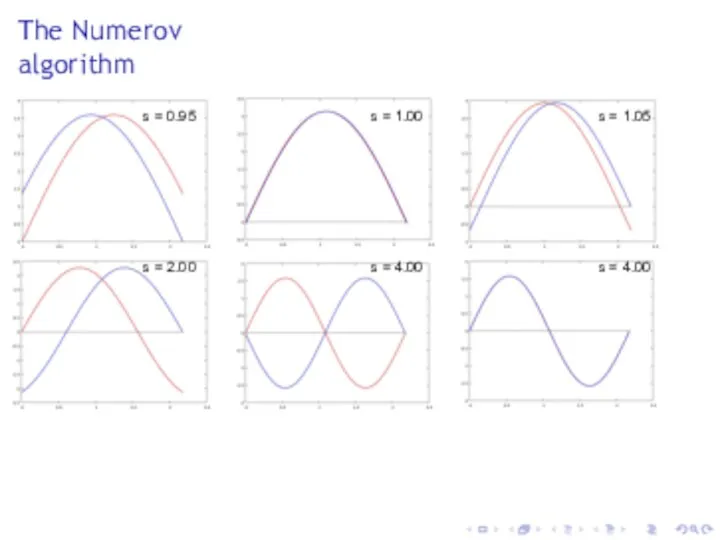
- 27. The Numerov algorithm s = 0.95 s = 1.00 s = 1.05 s = 2.00 s
- 29. Скачать презентацию












 Решение системы способом подстановки. 7 класс
Решение системы способом подстановки. 7 класс Адаптивные фильтры. Практическое применение (1)
Адаптивные фильтры. Практическое применение (1) Повторение материала по теме Обыкновенные дроби. 6 класс
Повторение материала по теме Обыкновенные дроби. 6 класс Площадь трапеции
Площадь трапеции Презентация Развитие математических способностей у детей дошкольного возраста
Презентация Развитие математических способностей у детей дошкольного возраста Математика. 1 класс. Урок 13. Число два. Цифра 2. Презентация
Математика. 1 класс. Урок 13. Число два. Цифра 2. Презентация Внеклассное мероприятие по информатике и математике. Викторина
Внеклассное мероприятие по информатике и математике. Викторина Математика. 1 класс. Урок 99. Сложение и вычитание в пределах 20 - Презентация
Математика. 1 класс. Урок 99. Сложение и вычитание в пределах 20 - Презентация Функции, пределы, непрерывности
Функции, пределы, непрерывности Методы искусственного базиса при решении ЗЛП. Лекция 3
Методы искусственного базиса при решении ЗЛП. Лекция 3 Многоугольники. Четырёхугольники
Многоугольники. Четырёхугольники Basics of functions and their graphs
Basics of functions and their graphs В стране сенсорики
В стране сенсорики Геометрические головоломки
Геометрические головоломки Платоновы тела
Платоновы тела Презентация к уроку по теме Закрепление изученного. Единицы измерения времени
Презентация к уроку по теме Закрепление изученного. Единицы измерения времени Кратные интегралы. (Лекция 3)
Кратные интегралы. (Лекция 3) Математическая мозаика
Математическая мозаика Деление на десятичную дробь. Правило деления
Деление на десятичную дробь. Правило деления Линейные уравнения (Алгебра – 7 класс). Электронный учебник
Линейные уравнения (Алгебра – 7 класс). Электронный учебник Дифференциальное исчисление функции одной переменной
Дифференциальное исчисление функции одной переменной Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Музыкальные инструменты для детей
Музыкальные инструменты для детей презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100
презентация к уроку математики по теме Периметр 2 класс по программе Школа 2100 Команда Умники и умницы
Команда Умники и умницы Образование чисел из одного десятка и нескольких единиц
Образование чисел из одного десятка и нескольких единиц Применение игровых технологий для развития и коррекции познавательных процессов на уроках математики в начальных классах
Применение игровых технологий для развития и коррекции познавательных процессов на уроках математики в начальных классах Умножение и деление
Умножение и деление