Содержание
- 2. Теоремы Чевы и Менелая «Обладая литературой более обширной, чем алгебра и арифметика вместе взятые, и по
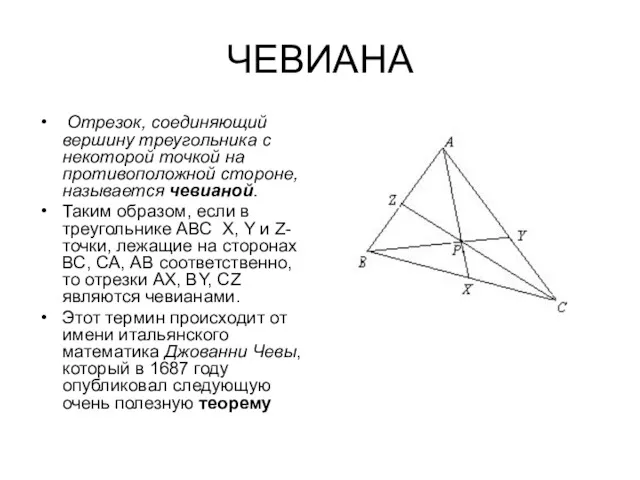
- 3. ЧЕВИАНА Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Таким образом, если
- 4. Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.
- 5. День рождения: 07.12.1647 года Дата смерти: 15.06.1734 года Гражданство: Италия Джованни Чева родился в 1647 году
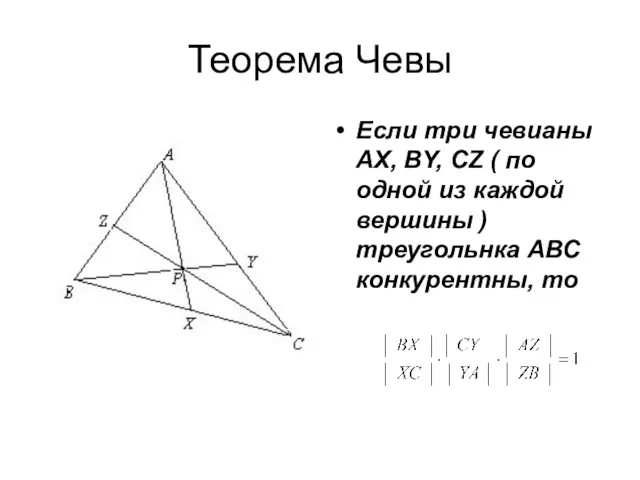
- 6. Теорема Чевы Если три чевианы АX, ВY, СZ ( по одной из каждой вершины ) треугольнка
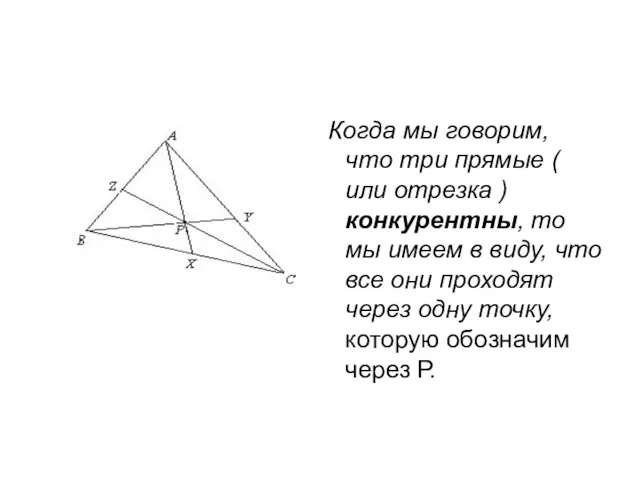
- 7. Когда мы говорим, что три прямые ( или отрезка ) конкурентны, то мы имеем в виду,
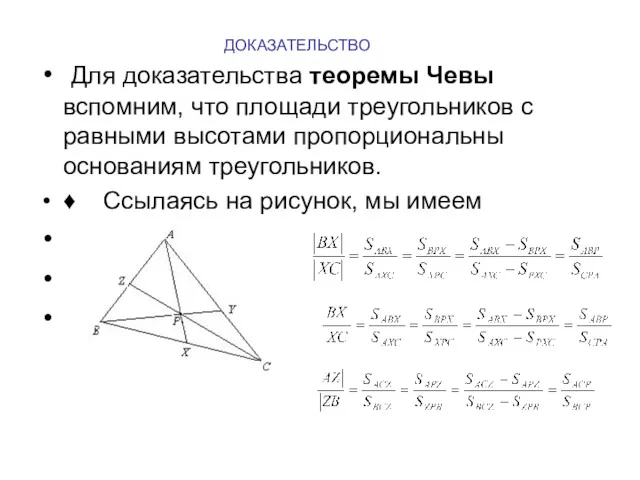
- 8. ДОКАЗАТЕЛЬСТВО Для доказательства теоремы Чевы вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников. ♦
- 9. Теперь, если мы перемножим их, то получим .
- 10. Рассмотрим доказательство некоторых следствий теоремы Чевы.
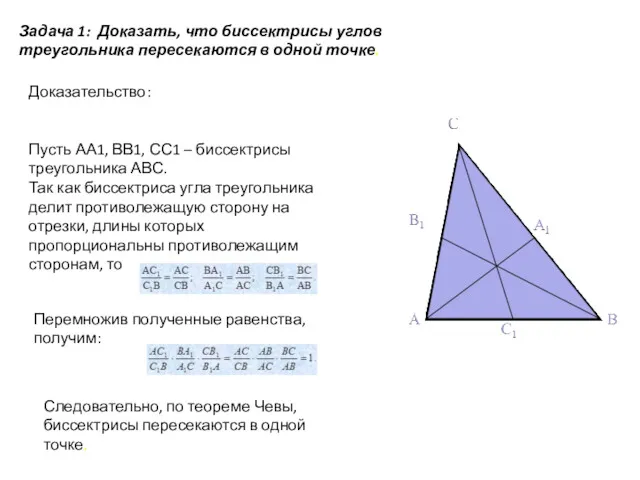
- 11. Задача 1: Доказать, что биссектрисы углов треугольника пересекаются в одной точке. Доказательство: Пусть АА1, ВВ1, СС1
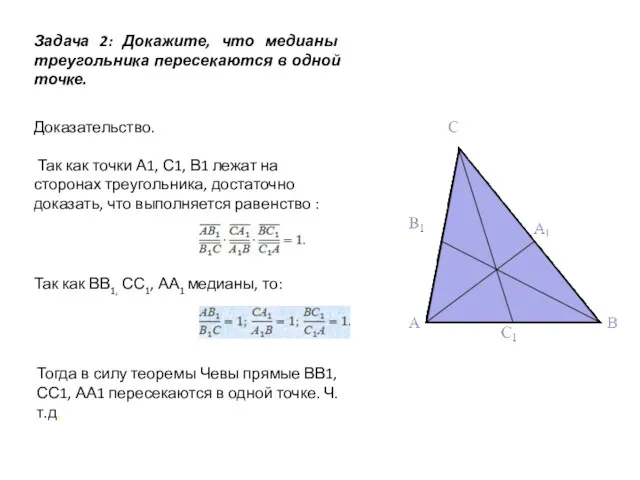
- 12. Задача 2: Докажите, что медианы треугольника пересекаются в одной точке. Доказательство. Так как точки А1, С1,
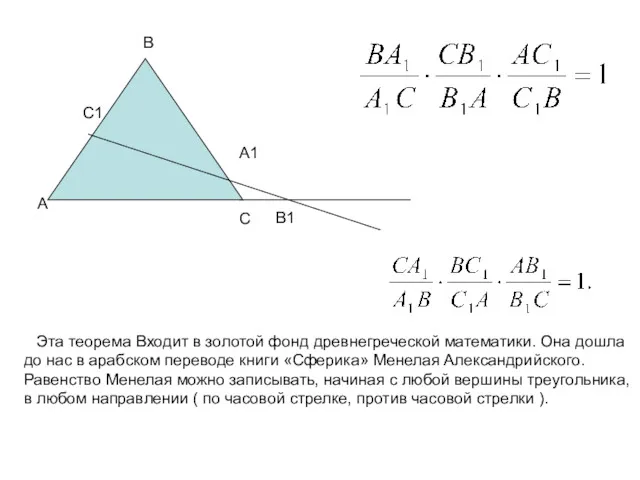
- 13. Теорема Менелая: Пусть точка А1 лежит на стороне ВС треугольника АВС, точка С1 – на стороне
- 14. А В1 В С А1 С1 Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла
- 15. Задача 1. В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN;
- 17. Скачать презентацию







 Алгебраические дроби, сокращение дробей
Алгебраические дроби, сокращение дробей Что такое топология
Что такое топология Числовые выражения
Числовые выражения Занимательная математика (5 класс)
Занимательная математика (5 класс) Возрастание и убывание функции. Экстремумы функции
Возрастание и убывание функции. Экстремумы функции Прямоугольный треугольник и его свойства
Прямоугольный треугольник и его свойства Невский проспект Санкт-Петербурга в цифрах. Зеленый мост на пересечении Невского проспекта и Мойки (часть 4)
Невский проспект Санкт-Петербурга в цифрах. Зеленый мост на пересечении Невского проспекта и Мойки (часть 4) Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Признаки равенства треугольников. Равнобедренный треугольник. Тест
Признаки равенства треугольников. Равнобедренный треугольник. Тест Системы счисления
Системы счисления Решение уравнений содержащих неизвестную под знаком модуля
Решение уравнений содержащих неизвестную под знаком модуля Математизация научных исследований в исторической науке
Математизация научных исследований в исторической науке 20230924_otkrytyy_urok_na_marafone_11_klass
20230924_otkrytyy_urok_na_marafone_11_klass Приёмы устных вычислений вида 470 + 80, 560 - 90
Приёмы устных вычислений вида 470 + 80, 560 - 90 Умножение десятичных дробей. Математика. 5 класс
Умножение десятичных дробей. Математика. 5 класс Нахождение числа по данному значению его дроби
Нахождение числа по данному значению его дроби Ділення десяткових дробів
Ділення десяткових дробів Сучасні методи наближення функцій багатьох змінних (інтерфлетація, інтерстріпація, інтерлокація)
Сучасні методи наближення функцій багатьох змінних (інтерфлетація, інтерстріпація, інтерлокація) Урок математики Сложение и вычитание двузначных чисел
Урок математики Сложение и вычитание двузначных чисел Логика высказываний
Логика высказываний Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Единицы длины
Единицы длины Длина окружности и длина дуги окружности
Длина окружности и длина дуги окружности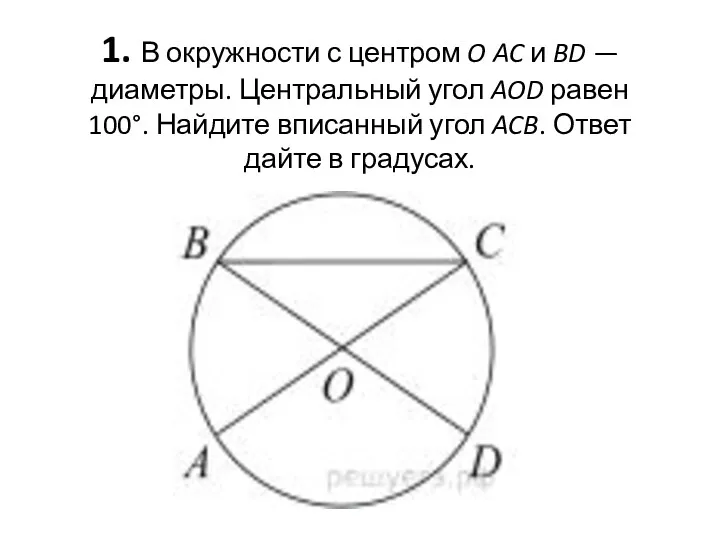 Окружности с центром O
Окружности с центром O Как люди научились считать
Как люди научились считать Дробно-рациональные уравнения
Дробно-рациональные уравнения Угол
Угол Состав чисел
Состав чисел