Содержание
- 2. Литература В.А. Горбатов Дискретная математика М.: АСТ; Астрель, 2003 Харари Ф. Теория графов, 2003г Кристофидес, Н.
- 3. Задача о Кёнигсбергских мостах Леонард Эйлер(1707-1783)
- 4. Основные объекты графов носитель метаграфа (конечное множество вершин). V={v1,v2, … vp} сигнатура метаграфа (конечное множество связей
- 5. Понятие графа и орграфа Граф G= , где V={v1,v2,…,vn}, n≥1 – множество вершин (носитель), U⊆V×V (сигнатура).
- 6. Неориентированный граф (граф) G = , V = {v1,v2,…,vn},n≥1, U⊆V×V (vi,vj) = (vj, vi) (vi,vj) –
- 7. Ориентированный граф (орграф) G= , V={v1,v2,…,vn},n≥1 U⊆V×V (vi,vj) ≠ (vj, vi) (vi,vj) - дуга
- 8. Геометрический граф Граф Орграф
- 9. Обозначение Gp,q ⏐V⏐= p, ⏐U⏐= q G1,0 - тривиальный граф
- 10. типы метаграфов ГИПЕРГРАФ (модельный граф) Сигнатура (U) - множество граней, каждая из которых связывает некоторое подмножество
- 11. взвешенные метаграфы f: V→N - весовая функция для носителя (вершин) g: U →K - весовая функция
- 12. Локальная структура графа (vi,vj)∈U – vi и vj – смежны uk= (vi,vj) – uk инцидентно vi,
- 13. Пример
- 14. Степень вершины Степень вершины (d(vi)) – число рёбер, инцидентных вершине d(v1)=2 d(v2)=2 d(v3)=3 d(v4)=1
- 15. Теорема В любом конечном графе число вершин нечётной степени чётно.
- 16. Свойства степеней графа Gp,q
- 17. Степень графа Степень графа (максимальная степень вершины) Минимальная степень вершины графа
- 18. Локальная структура ориентированного графа uk= (vi,vj) – дуга uk положительно инцидентна vi, дуга uk отрицательно инцидентна
- 19. Пример
- 20. Степени вершин в орграфе d+(vi) – число положительно инцидентных дуг вершины vi. d-(vi) – число отрицательно
- 21. Свойства степеней орграфа Для любого ориентированного графа
- 22. Свойства степеней орграфа Для любого ориентированного графа
- 23. Матричное представление графа Матрица смежности А:
- 24. Пример
- 25. Матрица инцидентности В
- 26. Пример
- 27. Матрица смежности орграфа А:
- 28. Пример
- 29. Матрица инцидентности В
- 30. Пример
- 31. Функциональный способ задания графов G= Г- функция окрестности вершин Г:V→P(V) Г(v)={vi ⎢ vi смежна с v}
- 32. Пример Г(v1)={v2, v3} Г(v2)={v1, v3} Г(v3)={v1, v2,v4} Г(v4)={v3}
- 33. Функциональный способ задания орграфов G= G= Г+, Г- - функции положительной и отрицательной полуокрестности вершины, соответственно
- 34. Пример Г(v1)+={v2, v3} Г(v2)+={v3} Г(v3)+={v2,v4} Г(v4)+=∅
- 35. Пример Г(v1)-=∅ Г(v2)- ={v1,v3} Г(v3) -={v1,v2} Г(v4)-={v3}
- 36. Изоморфизм графов Графы изоморфны, если существует взаимно однозначное соответствие между множествами вершин, сохраняющее отношение смежности
- 37. Функциональное задание изоморфизма графов Два графа Ga=〈Va,Ua〉 и Gb=〈Vb,Ub〉 изоморфны, если существует взаимно однозначная функция h:
- 38. Свойства изоморфизма Отношение рефлексивно симметрично транзитивно Эквивалентность
- 39. Пример изоморфных графов
- 40. Пример не изоморфных графов
- 41. Инварианты графа Количественная или качественная характеристики, неизменные для всех изоморфных между собой графов (орграфов) называется ИНВАРИАНТОМ
- 42. Полный граф Kn Граф полный, если каждая вершина смежна с каждой. Полный граф с n вершинами
- 43. Двудольный граф Граф двудольный, если множество вершин графа можно разбить на два непересекающихся подмножества, в каждом
- 44. Двудольные графы. Примеры
- 45. Полный двудольный граф Km,n Km,n - граф двудольный и каждая вершина из множества V1 смежна с
- 46. Полные двудольные графы Km,n
- 47. Операции над графами Удаление ребра G= , G\u=
- 48. Удаление вершины G= , G\v= V’=V\{v}, U’=U∩(V’× V’)
- 49. Подграфы G’= - подграф графа G= , если V’⊆V, U’=U∩(V’× V’) (порождённый подграф)
- 50. Подграфы G’= - частичный подграф графа G= , если V’⊆V, U’⊆U∩(V’× V’) (частичный граф, подграф)
- 51. Дополнение графа
- 53. Скачать презентацию
 Числа и вычисления. Задание для устного счета
Числа и вычисления. Задание для устного счета Решение системы уравнений методом Гаусса
Решение системы уравнений методом Гаусса Поэзия в математике
Поэзия в математике Рациональные неравенства
Рациональные неравенства Урок постановки учебной задачи в системе РО
Урок постановки учебной задачи в системе РО Моделирование временных рядов. (Лекция 8)
Моделирование временных рядов. (Лекция 8) Проверка гипотез относительно возможных значений коэффициентов МЛРМ
Проверка гипотез относительно возможных значений коэффициентов МЛРМ Конспект совместной деятельности с детьми подготовительной к школе группы по познавательному развитию (ФЭМП).
Конспект совместной деятельности с детьми подготовительной к школе группы по познавательному развитию (ФЭМП).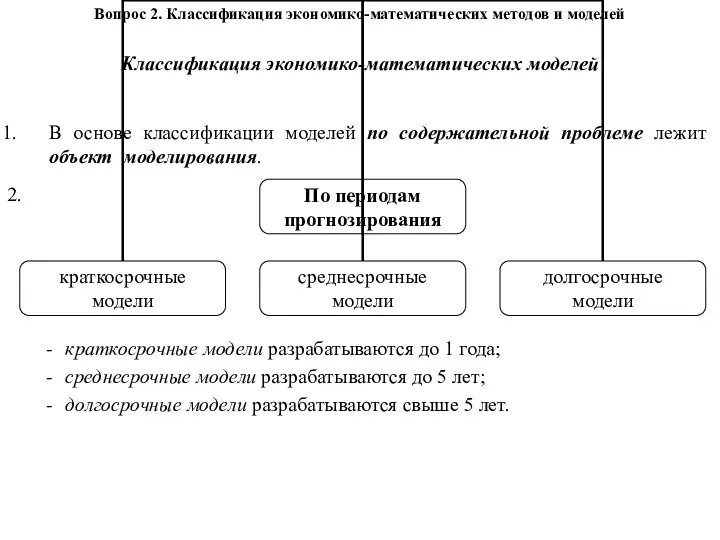 Классификация экономико-математических моделей
Классификация экономико-математических моделей Нормальный закон распределения. (Тема 6)
Нормальный закон распределения. (Тема 6) Задачи на движение. ЕГЭ, математика
Задачи на движение. ЕГЭ, математика Дециметр урок математики в 1 классе
Дециметр урок математики в 1 классе Игры на развитие математических способностей детей младшего дошкольного возраста.
Игры на развитие математических способностей детей младшего дошкольного возраста. Ломаная
Ломаная Смежные углы
Смежные углы Умножение. Распределительное свойство. (математика, 3 класс. УМК Гармония).
Умножение. Распределительное свойство. (математика, 3 класс. УМК Гармония). Таблица умножения достойна уважения.
Таблица умножения достойна уважения. Определение конуса
Определение конуса Логическое мышление, его развитие при обучении математике
Логическое мышление, его развитие при обучении математике Методика формирования элементарных математических представлений как научная область
Методика формирования элементарных математических представлений как научная область Математика. Строительство
Математика. Строительство Задачи на умножение и деление
Задачи на умножение и деление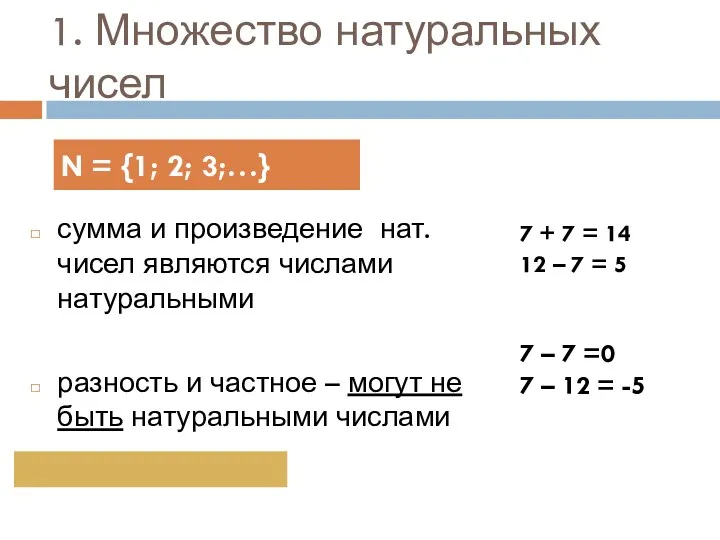 Множество натуральных чисел
Множество натуральных чисел Многоугольник. Выпуклый многоугольник. Четырехугольник
Многоугольник. Выпуклый многоугольник. Четырехугольник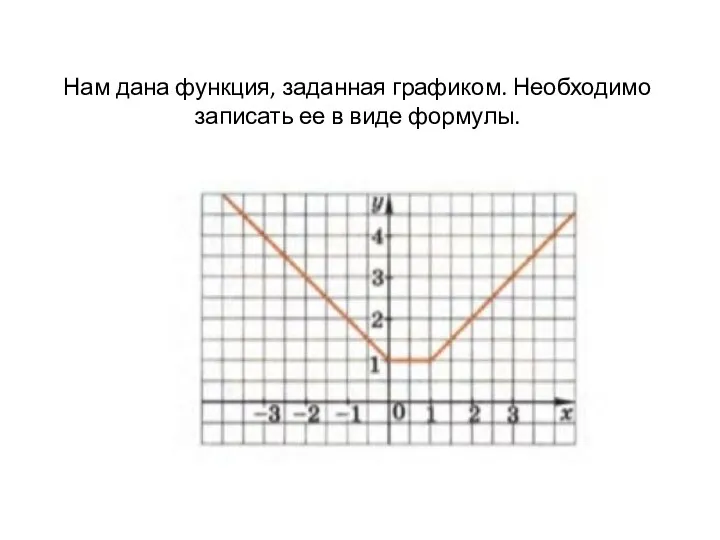 функция, заданная графиком
функция, заданная графиком Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Неевклидова геометрия
Неевклидова геометрия Қайталау (Мектепалды даярлық тобы)
Қайталау (Мектепалды даярлық тобы)