Содержание
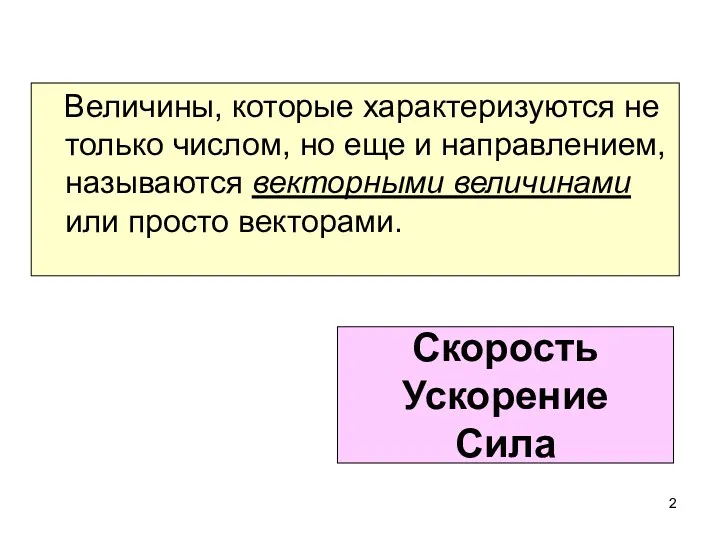
- 2. Скорость Ускорение Сила Величины, которые характеризуются не только числом, но еще и направлением, называются векторными величинами
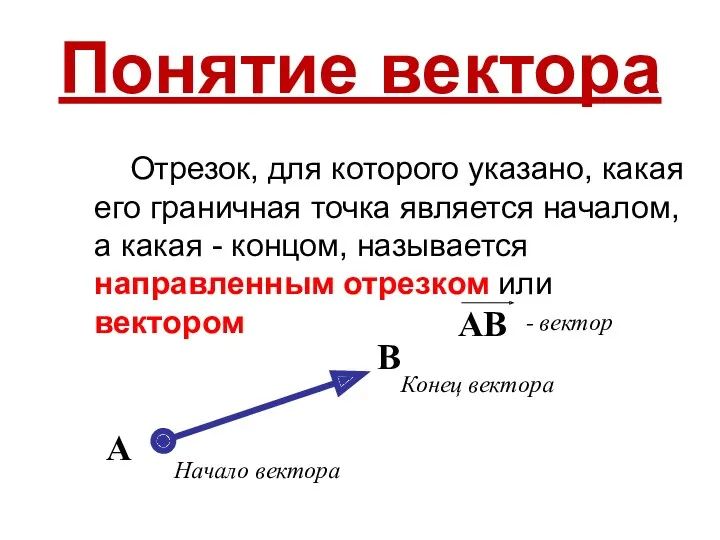
- 3. Понятие вектора Отрезок, для которого указано, какая его граничная точка является началом, а какая - концом,
- 4. Вектор характеризуется следующими элементами: 1. начальной точкой (точкой приложения); 2. направлением; 3. длиной («модулем вектора»).
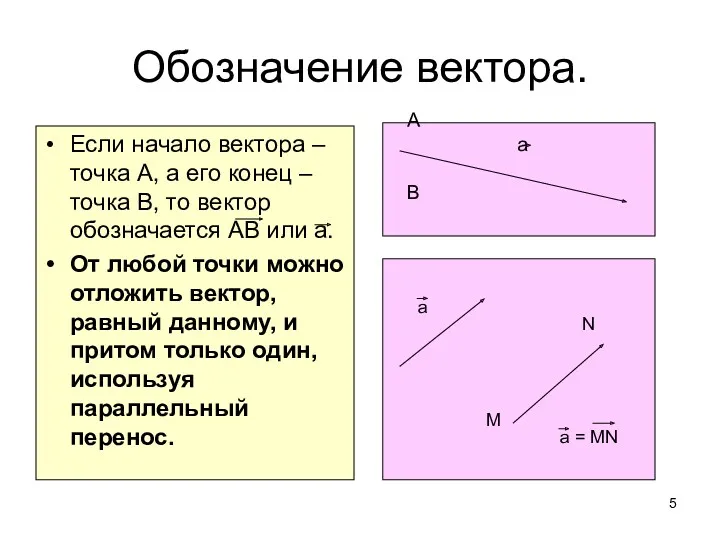
- 5. Если начало вектора – точка А, а его конец – точка В, то вектор обозначается АВ
- 6. Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет
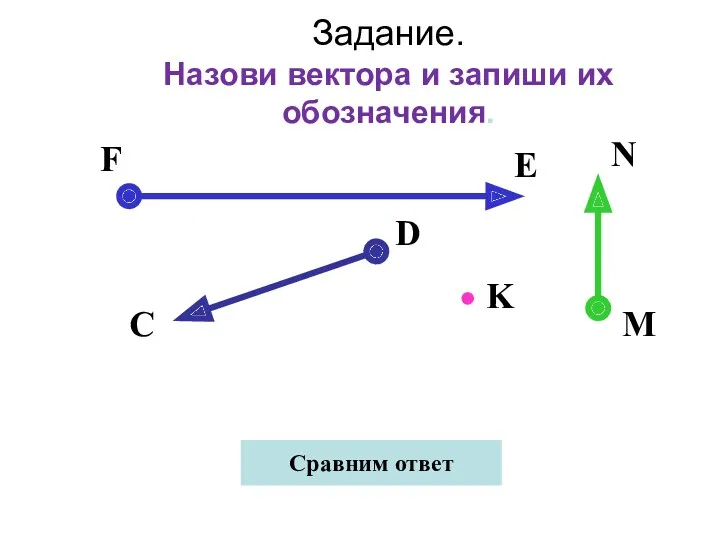
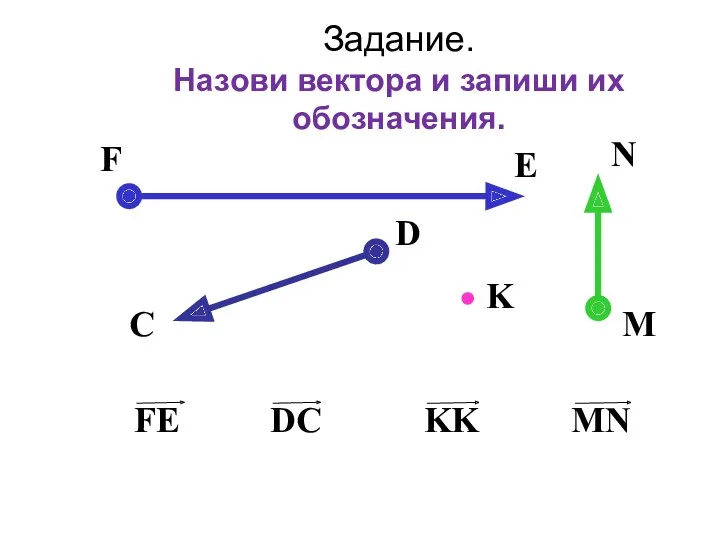
- 7. Задание. Назови вектора и запиши их обозначения. Сравним ответ
- 8. Задание. Назови вектора и запиши их обозначения.
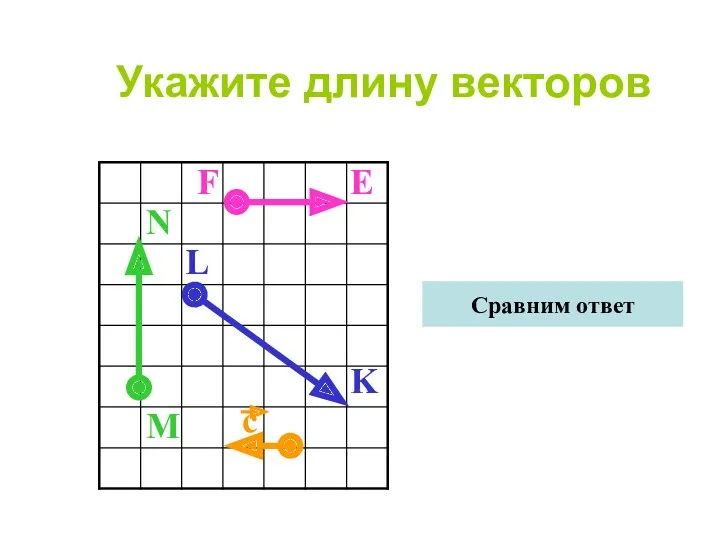
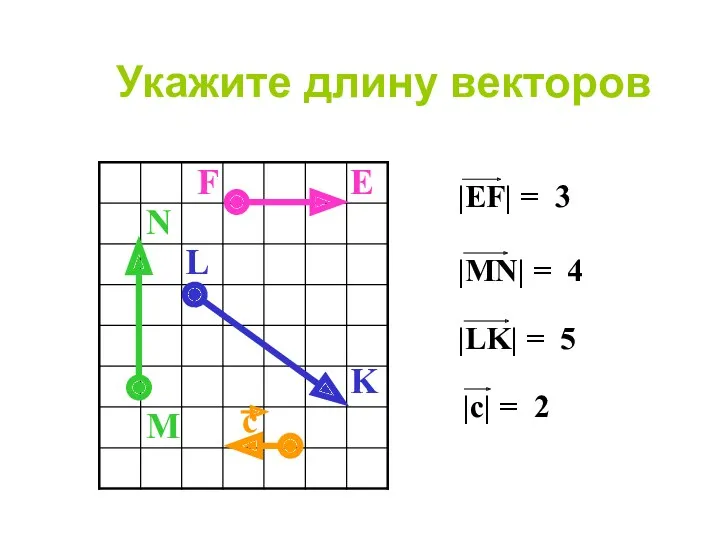
- 9. Укажите длину векторов M N F E L K Сравним ответ
- 10. Укажите длину векторов
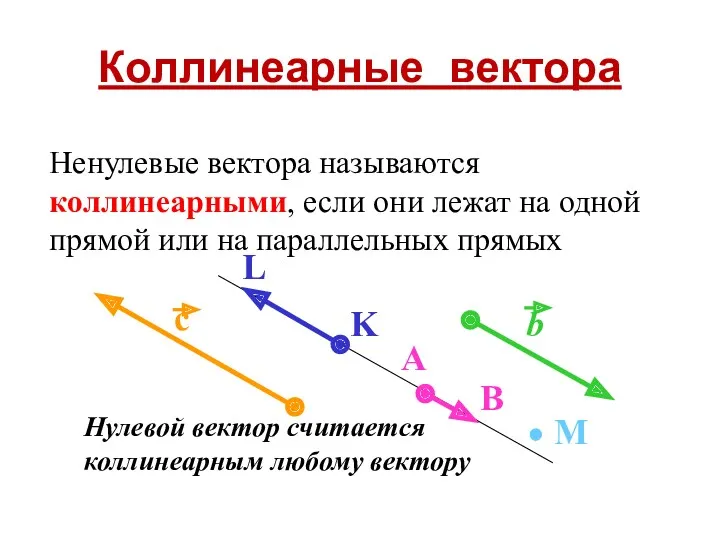
- 11. Нулевой вектор считается коллинеарным любому вектору Коллинеарные вектора Ненулевые вектора называются коллинеарными, если они лежат на
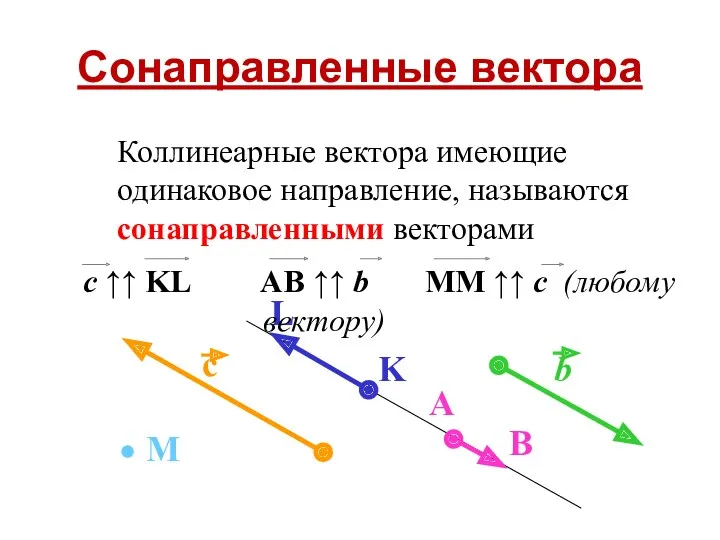
- 12. Сонаправленные вектора Коллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторами
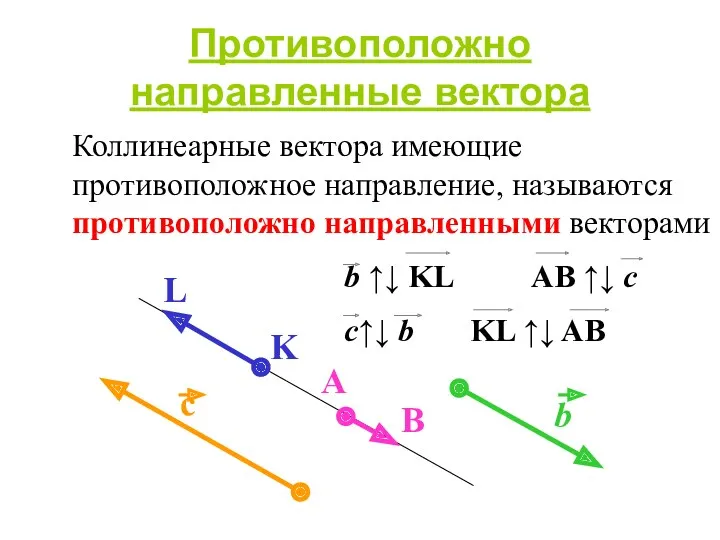
- 13. Противоположно направленные вектора Коллинеарные вектора имеющие противоположное направление, называются противоположно направленными векторами
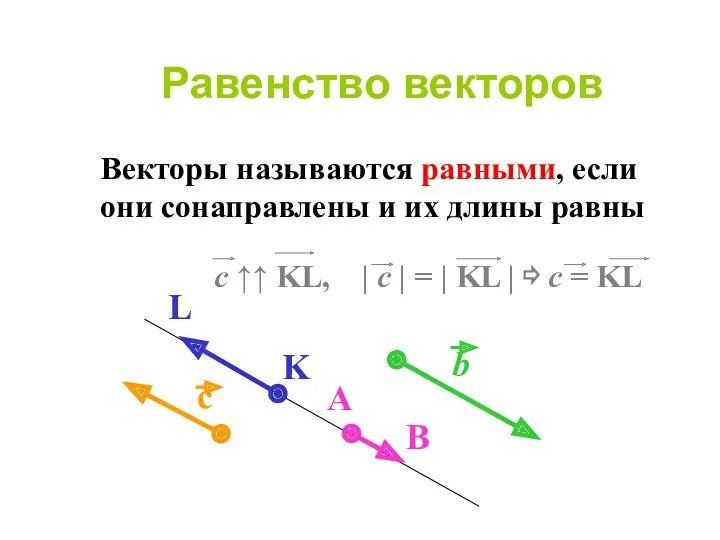
- 14. Равенство векторов Векторы называются равными, если они сонаправлены и их длины равны
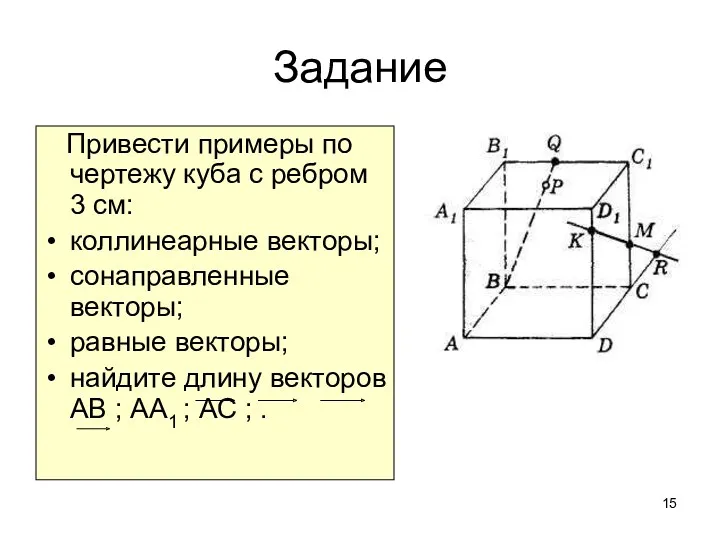
- 15. Задание Привести примеры по чертежу куба с ребром 3 см: коллинеарные векторы; сонаправленные векторы; равные векторы;
- 16. Действия над векторами
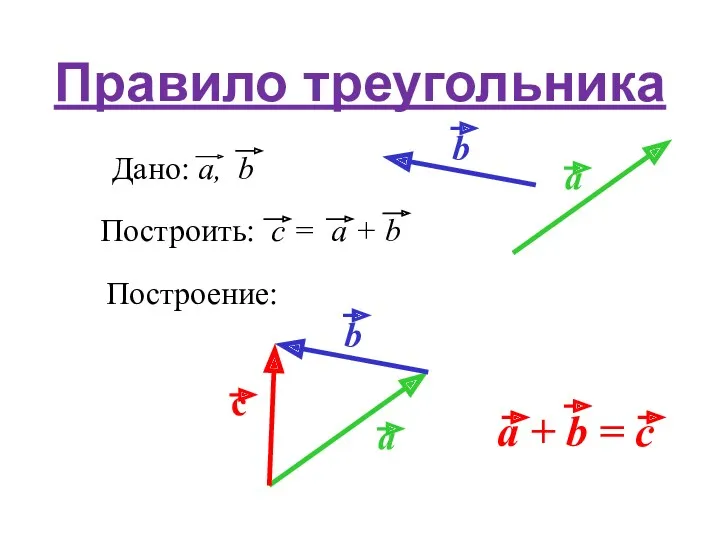
- 17. Сложение векторов Правило треугольника Правило параллелограма Сложение коллинеарных векторов
- 18. Правило треугольника Построение:
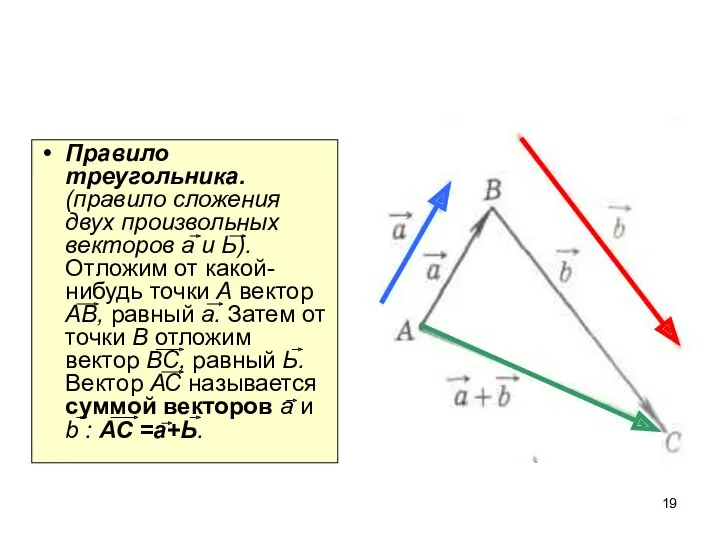
- 19. Правило треугольника. (правило сложения двух произвольных векторов а и Ь). Отложим от какой-нибудь точки А вектор
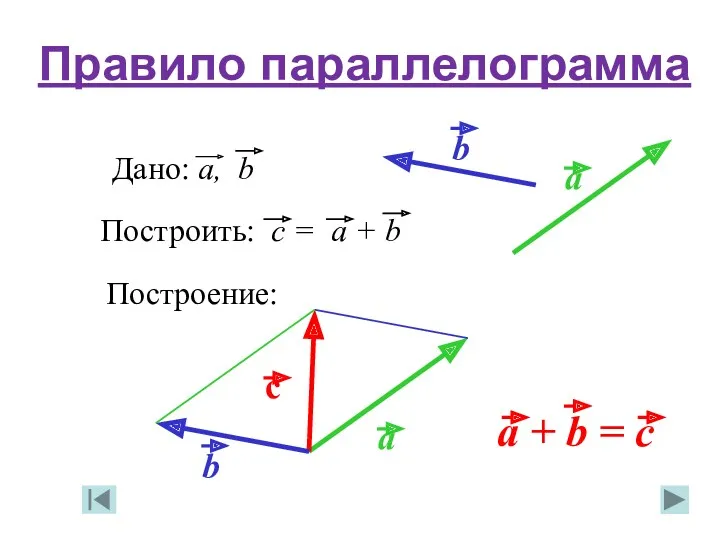
- 20. Правило параллелограмма Построение:
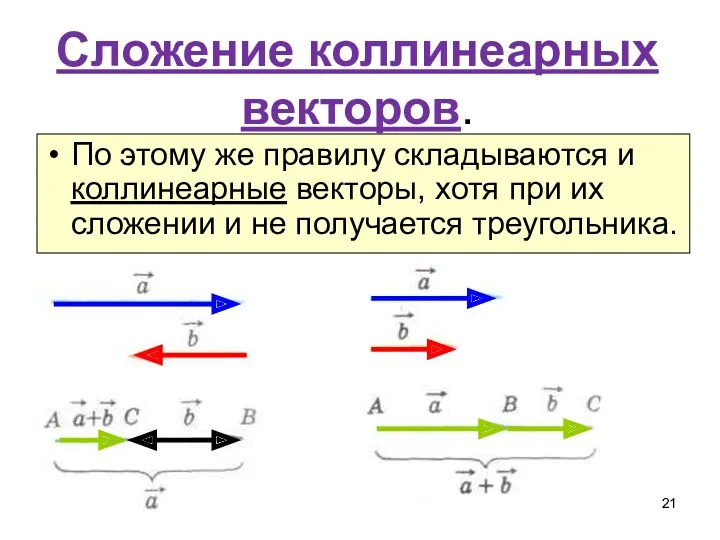
- 21. Сложение коллинеарных векторов. По этому же правилу складываются и коллинеарные векторы, хотя при их сложении и
- 22. Свойства сложения векторов. Для любых векторов а, b и с справедливы равенства: а + b =
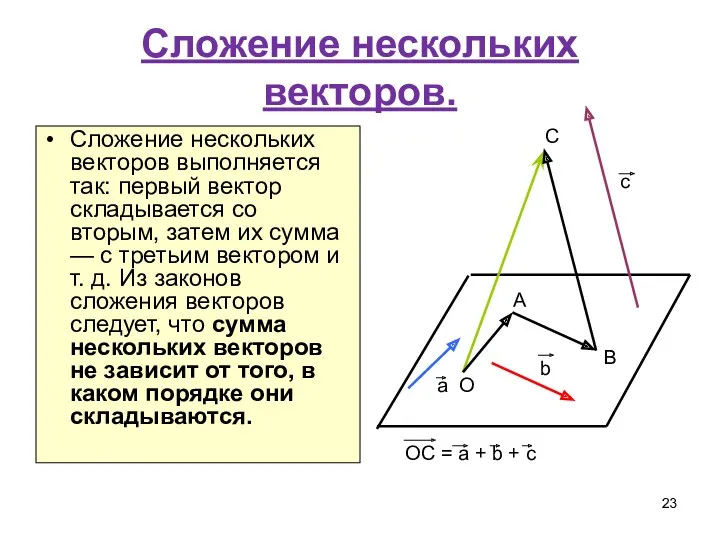
- 23. Сложение нескольких векторов. Сложение нескольких векторов выполняется так: первый вектор складывается со вторым, затем их сумма
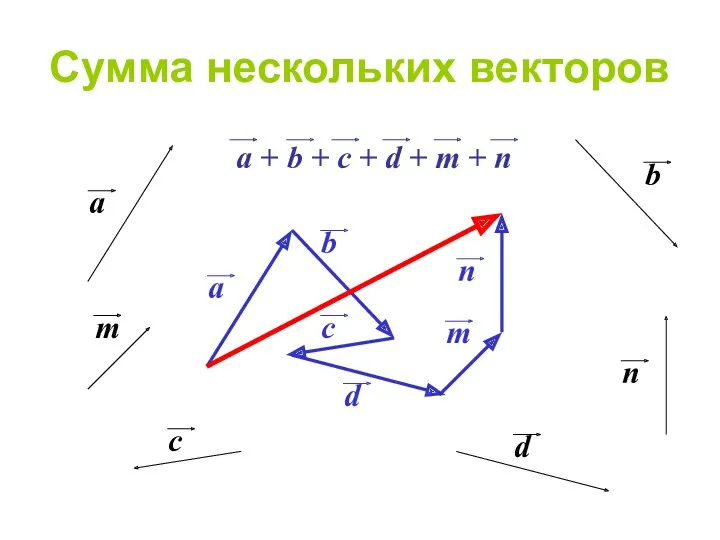
- 24. Сумма нескольких векторов
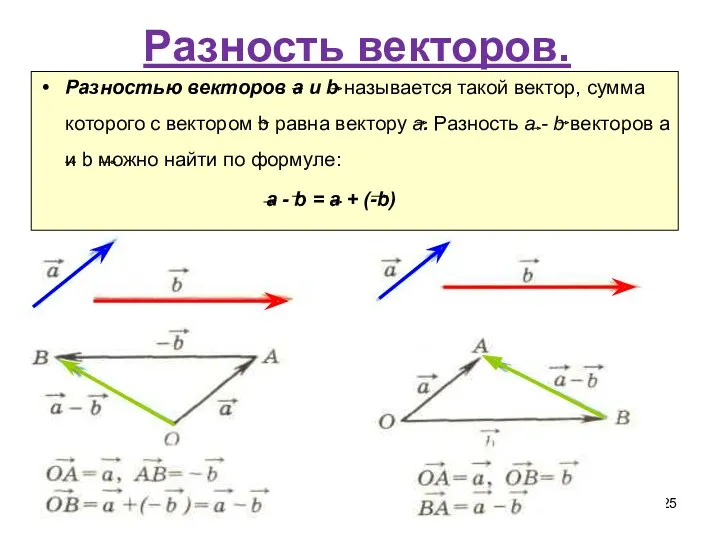
- 25. Разность векторов. Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна
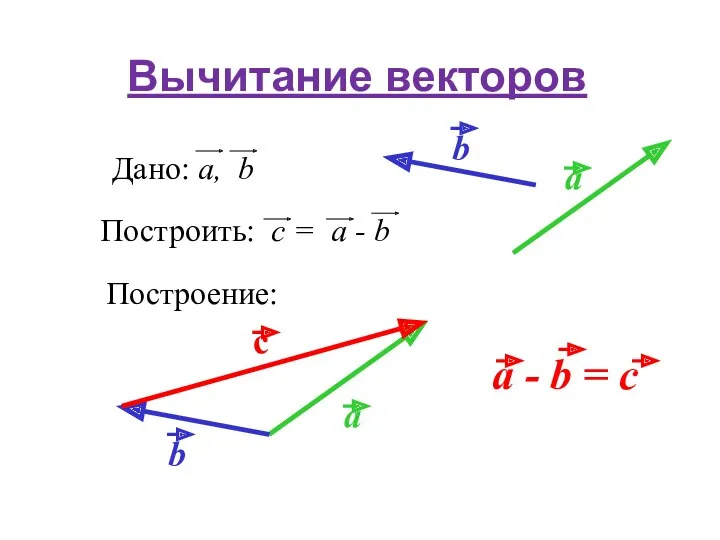
- 26. Вычитание векторов Построение:
- 27. Умножение вектора a на число k k·a = b, |a| ≠ 0, k – произвольное число
- 28. Правила умножения вектора на число. Для любых векторов а, b и любых чисел k, т справедливы
- 29. Свойства умножения вектора на число. (-1)а является вектором, противоположным вектору а, т.е. (-1)a = -а. если
- 30. Произведением нулевого вектора на любое число считается нулевой вектор. Для любого числа k и любого вектора
- 31. Декартовая система координат
- 32. Рене Декарт французский философ, математик, физик и физиолог. Заложил основы аналитической геометрии, дал понятия переменной величины
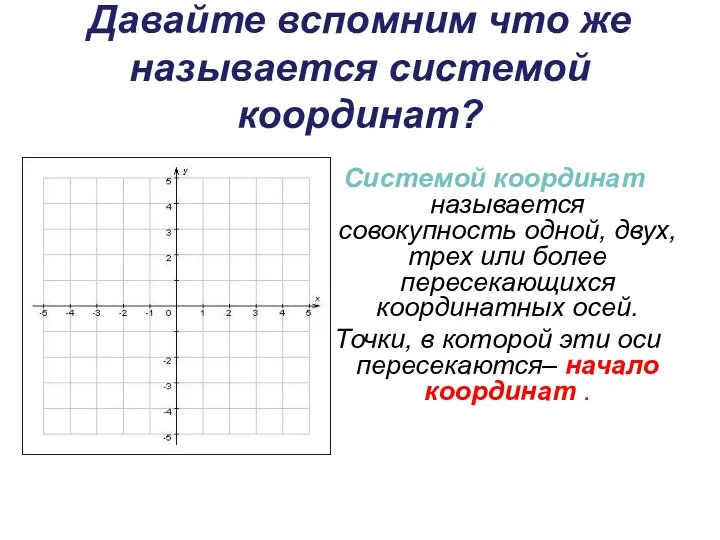
- 33. Давайте вспомним что же называется системой координат? Системой координат называется совокупность одной, двух, трех или более
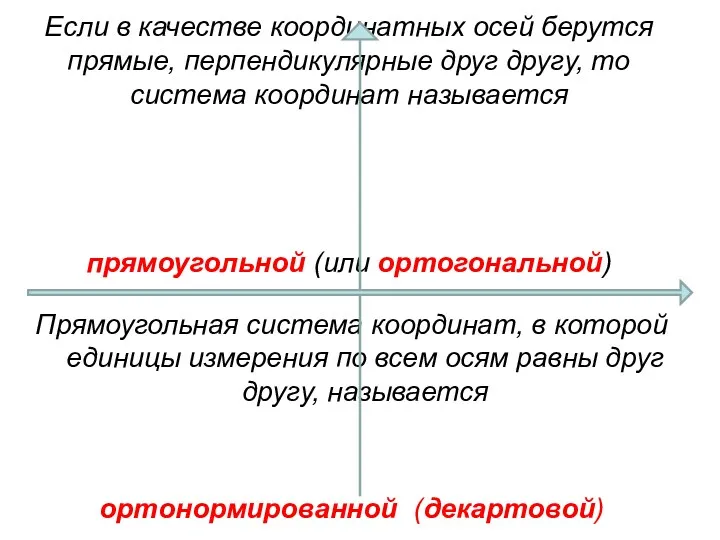
- 34. Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или
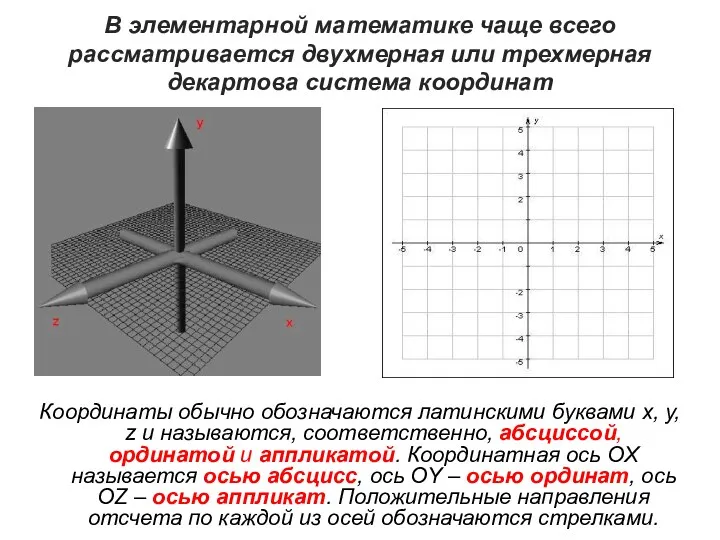
- 35. В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат Координаты обычно обозначаются латинскими
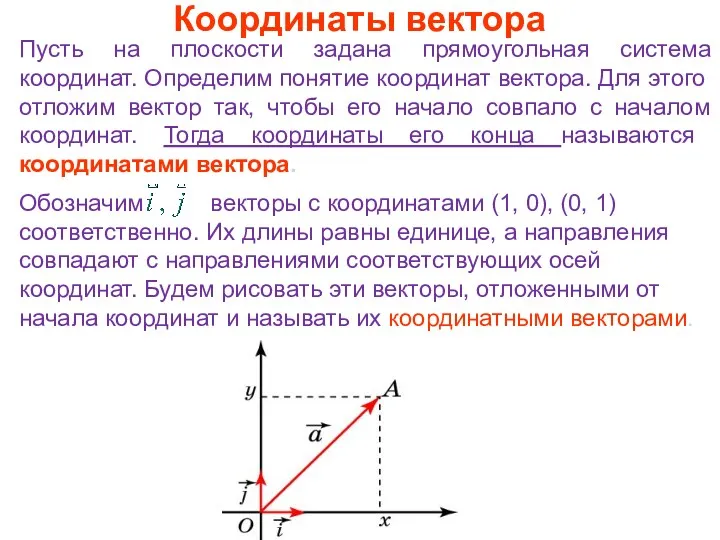
- 36. Координаты вектора Пусть на плоскости задана прямоугольная система координат. Определим понятие координат вектора. Для этого отложим
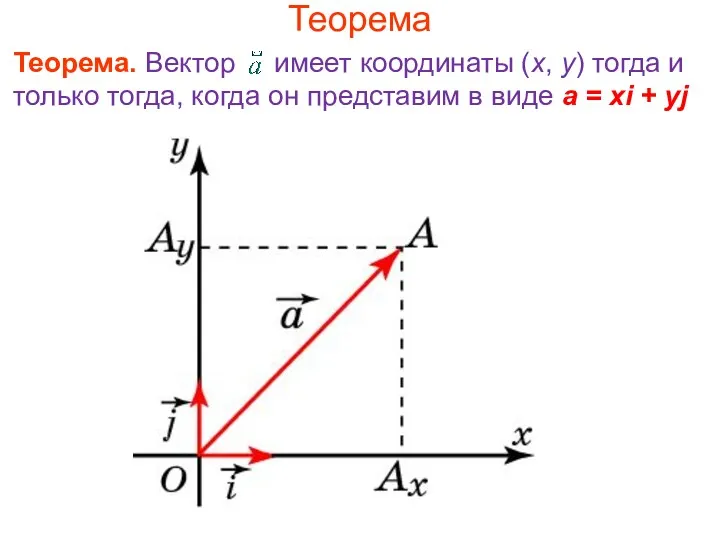
- 37. Теорема Теорема. Вектор имеет координаты (x, y) тогда и только тогда, когда он представим в виде
- 38. Пример
- 39. Упражнение 1
- 40. Упражнение 2
- 41. Упражнение 3
- 42. Упражнение 4
- 43. Упражнение 5
- 44. Упражнение 6
- 45. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2
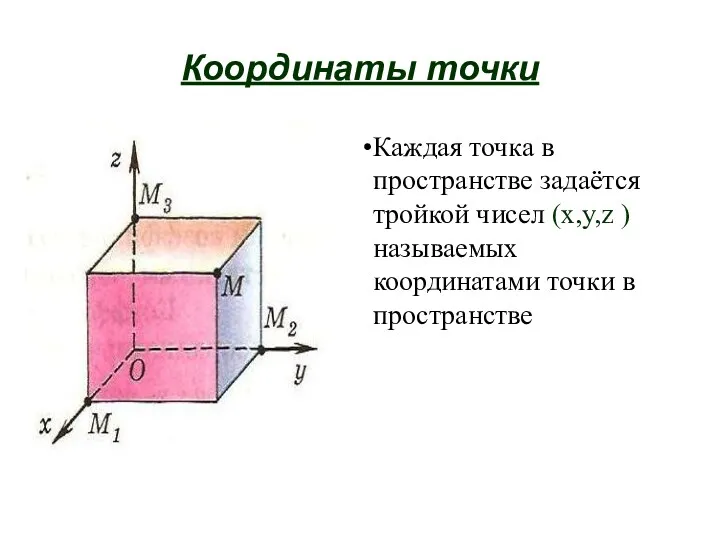
- 46. Координаты точки Каждая точка в пространстве задаётся тройкой чисел (x,y,z ) называемых координатами точки в пространстве
- 47. Координаты вектора Векторы (i. j. k) единичные векторы Любой вектор можно разложить по координатным векторам Назад
- 48. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2 + z1z2
- 49. Пример №1 Найти скалярное произведение векторов: a {-6; 9} b {-1; 0}
- 50. Пример №2 Найти скалярное произведение векторов: a {0; 0; 4} b {22; 1; 8}
- 51. Пример №3 Найти скалярное произведение векторов: a {1; 7; 9} b {-2; 4; 0}
- 52. Проверочная работа 1. Найти скалярное произведение векторов: a {1; 10; 7} b {0; 7; 0}
- 53. Проверочная работа 2. Найти скалярное произведение векторов: a {7; 25; 0} b {11; 0; 54}
- 54. Проверочная работа 3. Найти скалярное произведение векторов: a {-1; 2; 8} b {5; 5; 0}
- 55. Скалярное произведение векторов (через длину векторов и угол между ними)
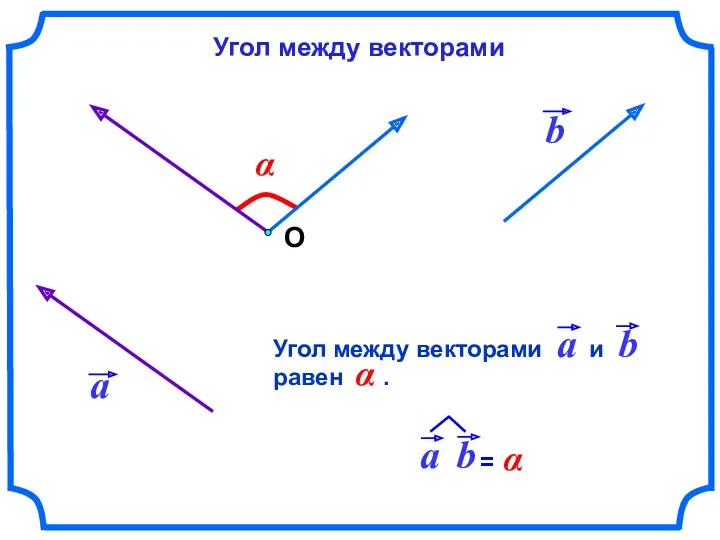
- 56. α О Угол между векторами
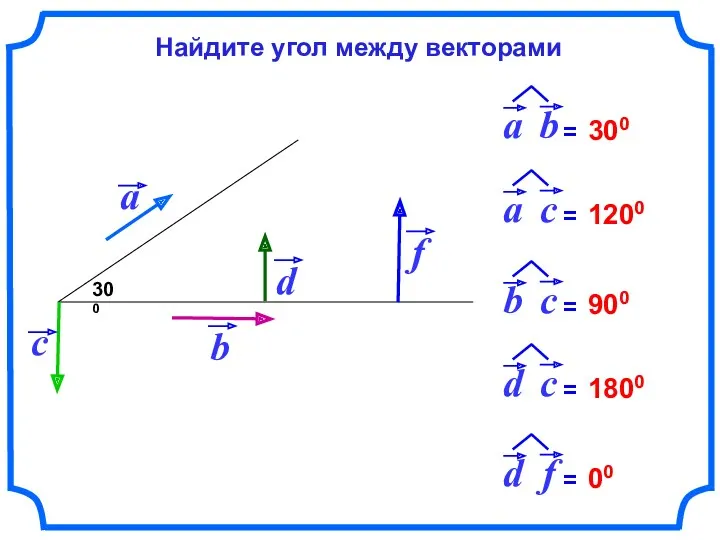
- 57. 300 300 1200 900 1800 00 Найдите угол между векторами
- 58. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
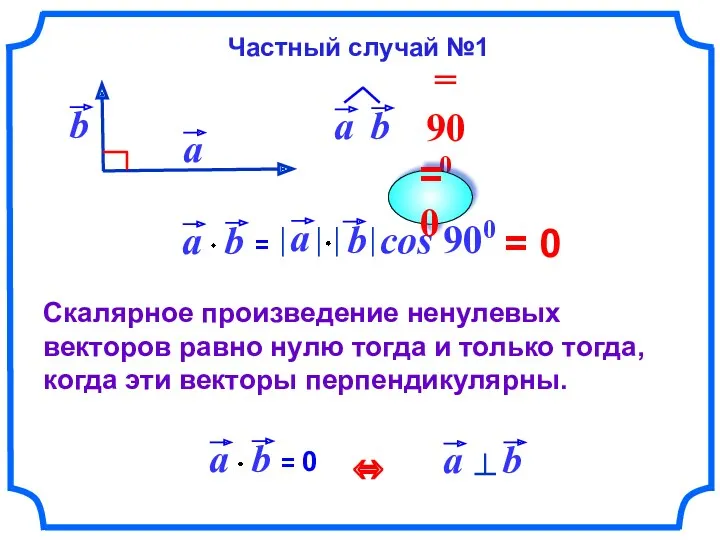
- 59. = 0 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
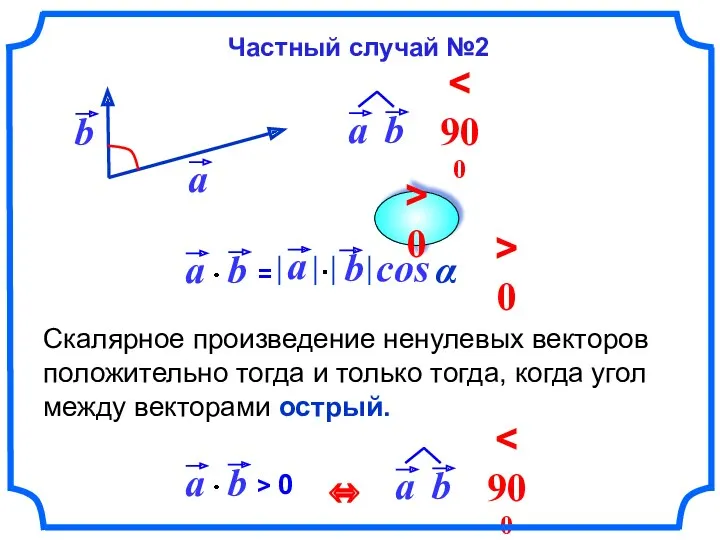
- 60. Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. cos α
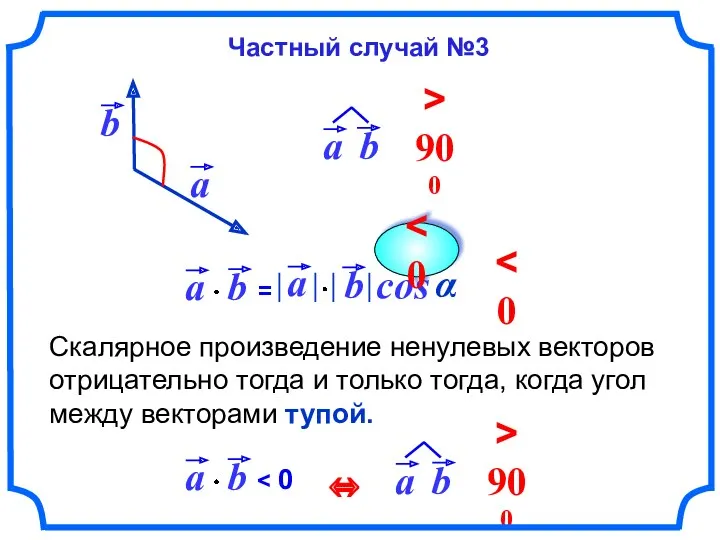
- 61. Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. cos α
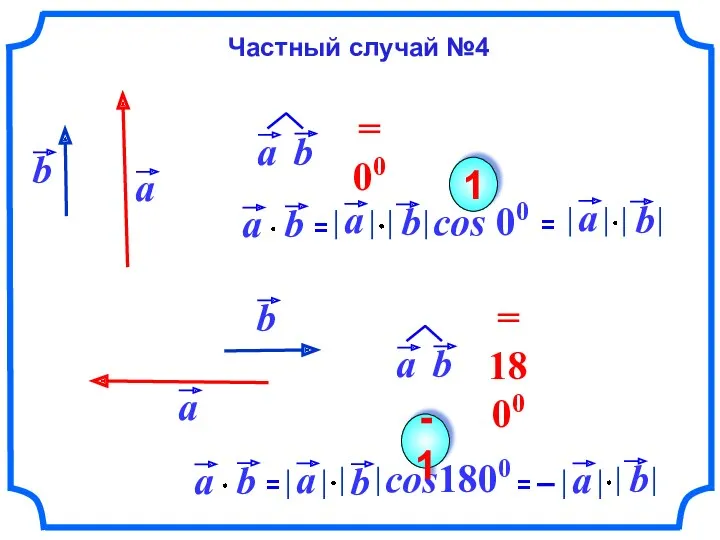
- 62. cos 00 1 cos1800 -1 Частный случай №4
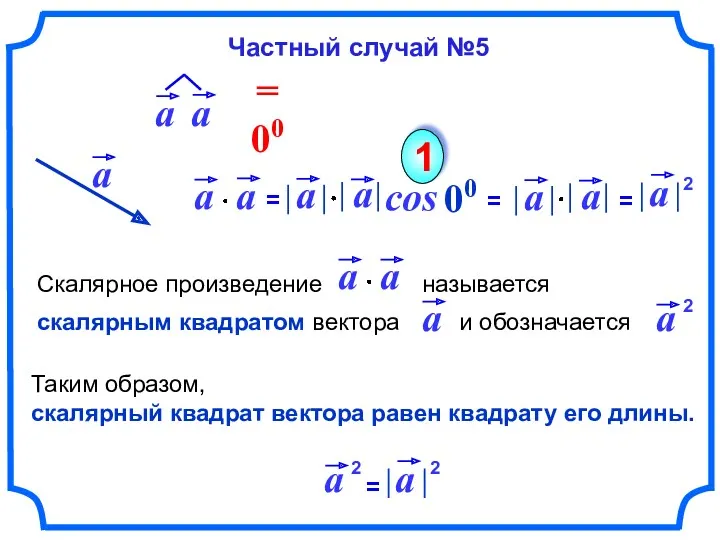
- 63. cos 00 1 Таким образом, скалярный квадрат вектора равен квадрату его длины. Частный случай №5 2
- 64. Формула для нахождения скалярного произведения через координаты векторов = x1x2 + y1y2
- 66. Скачать презентацию






























 Презентация к уроку математики Сравнение чисел
Презентация к уроку математики Сравнение чисел Компоненты при сложении. Перестановка слагаемых
Компоненты при сложении. Перестановка слагаемых Делители и кратные (тест)
Делители и кратные (тест) Арифметикалық прогрессияда
Арифметикалық прогрессияда Парабола и ее применение
Парабола и ее применение Квадратный корень из дроби
Квадратный корень из дроби Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Правильный многоугольник
Правильный многоугольник Формула Тейлора
Формула Тейлора Тригонометрические уравнения
Тригонометрические уравнения Методы решения текстовых задач
Методы решения текстовых задач Приёмы устного решения квадратного уравнения. Подготовка к экзаменам в тестовой форме
Приёмы устного решения квадратного уравнения. Подготовка к экзаменам в тестовой форме Периметр прямоугольника
Периметр прямоугольника Моделирование временных рядов. (Лекция 8)
Моделирование временных рядов. (Лекция 8) Системы линейных уравнений и методы их решения. (Тема 2)
Системы линейных уравнений и методы их решения. (Тема 2) Логические величины и выражения
Логические величины и выражения Решение задач с помощью уравнений
Решение задач с помощью уравнений Окружность. Отличие круга от окружности
Окружность. Отличие круга от окружности Математическая игра Цифра семь известна всем
Математическая игра Цифра семь известна всем Правильні многогранники
Правильні многогранники Урок математики. Сутки. Время от 0 до 24
Урок математики. Сутки. Время от 0 до 24 Определители
Определители Путешествие в страну Геометрию: Прямой угол
Путешествие в страну Геометрию: Прямой угол Час веселой математики. Внеклассное мероприятие для 5-6 классов
Час веселой математики. Внеклассное мероприятие для 5-6 классов Закрепление. Величины (Методическая разработка)
Закрепление. Величины (Методическая разработка) Практикум по решению задачи №20 (базовый уровень)
Практикум по решению задачи №20 (базовый уровень) Приёмы быстрого счёта
Приёмы быстрого счёта Урок математики 1 класс УМК ПНШ. Число и цифра 3
Урок математики 1 класс УМК ПНШ. Число и цифра 3