Содержание
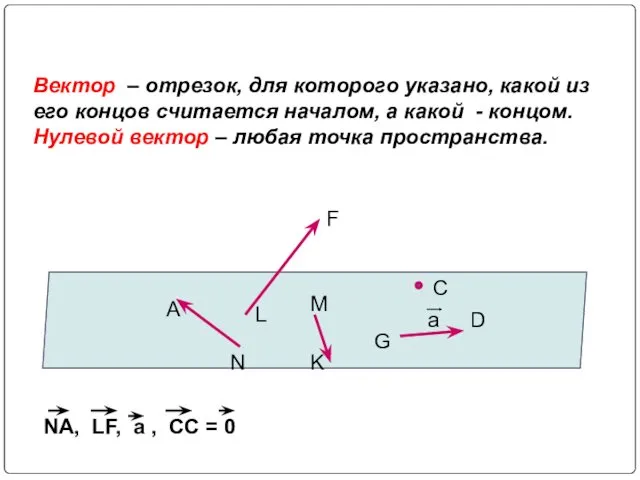
- 2. C F G D A N M K L Вектор – отрезок, для которого указано, какой
- 3. Длиной ненулевого вектора АВ называется длина отрезка АВ Обозначение : | a | или | АВ
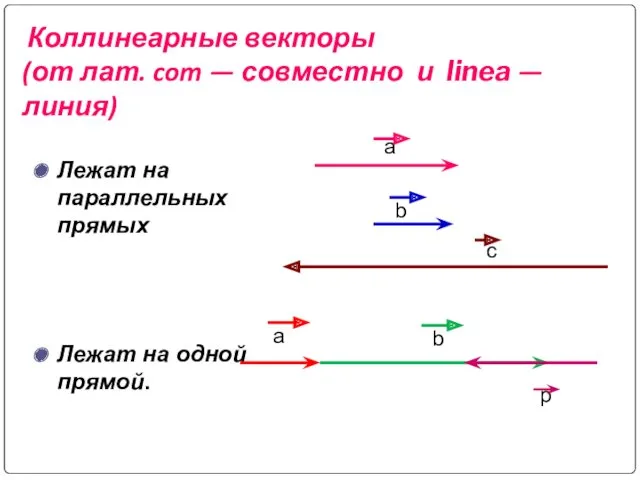
- 4. Коллинеарные векторы (от лат. com — совместно и linea — линия) Лежат на параллельных прямых Лежат
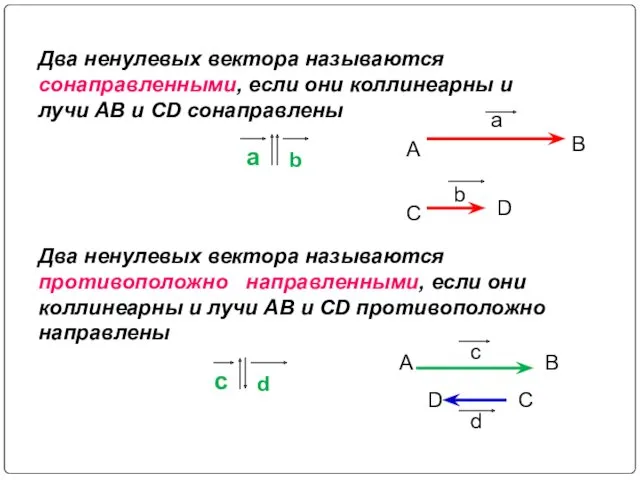
- 5. a b c d a b Два ненулевых вектора называются сонаправленными, если они коллинеарны и лучи
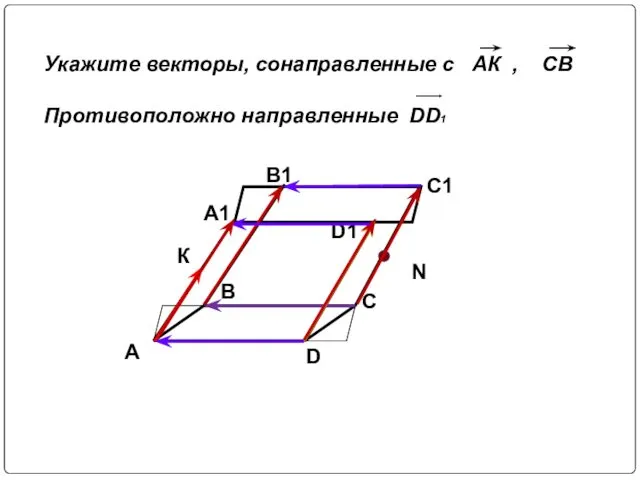
- 6. A D C B A1 B1 C1 D1 Укажите векторы, сонаправленные с АК , СВ Противоположно
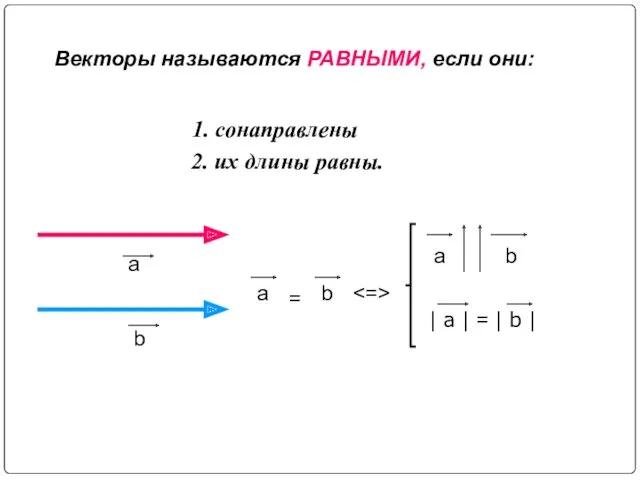
- 7. 1. сонаправлены 2. их длины равны. a b | a | = | b | a
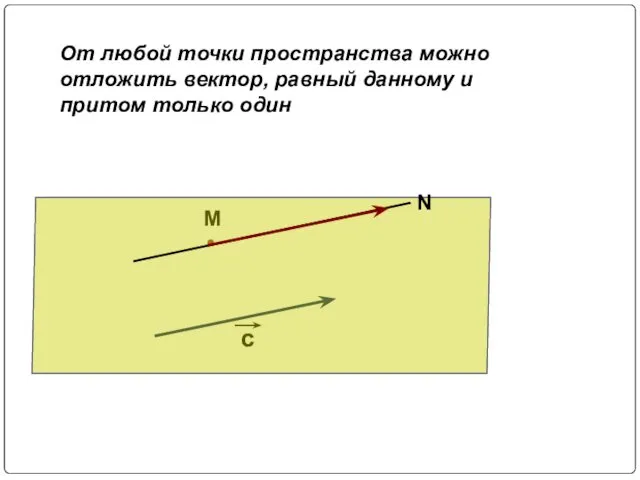
- 8. M c От любой точки пространства можно отложить вектор, равный данному и притом только один N
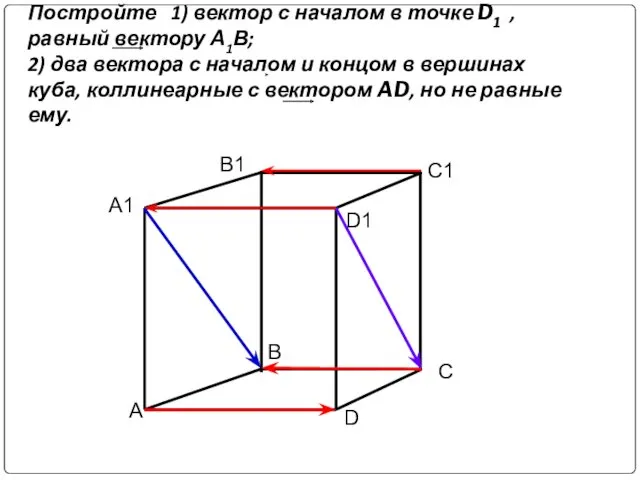
- 9. Постройте 1) вектор с началом в точке D1 , равный вектору А1В; 2) два вектора с
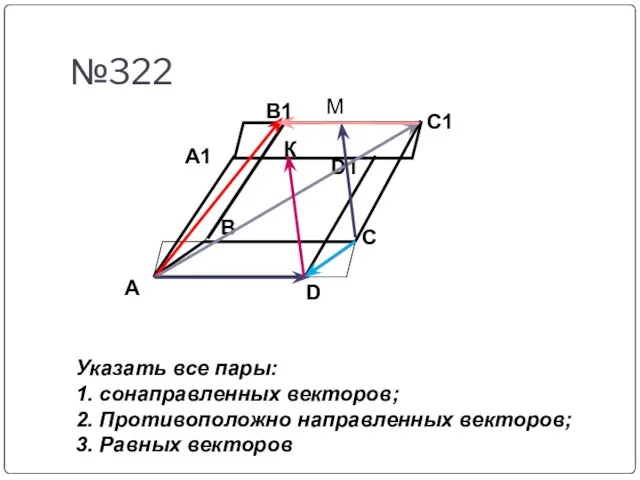
- 10. №322 A D C B A1 B1 C1 D1 К М Указать все пары: 1. сонаправленных
- 11. § 2 СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
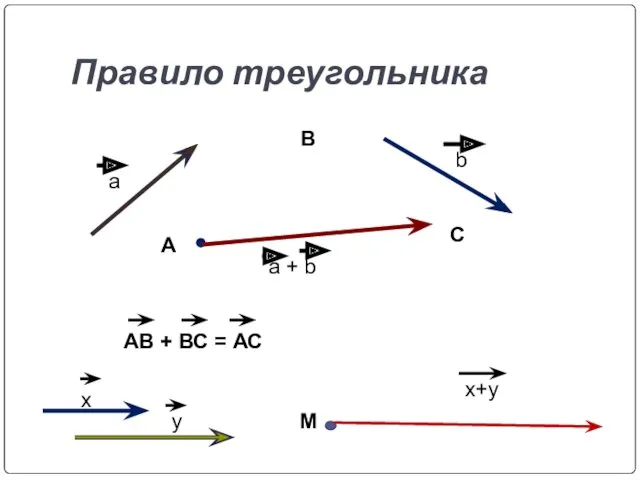
- 12. Правило треугольника a b a + b А M x y x+y В С АВ +
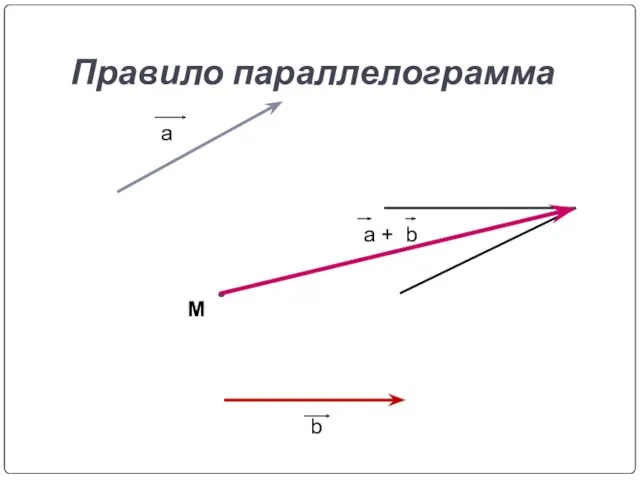
- 13. Правило параллелограмма a b a + b M
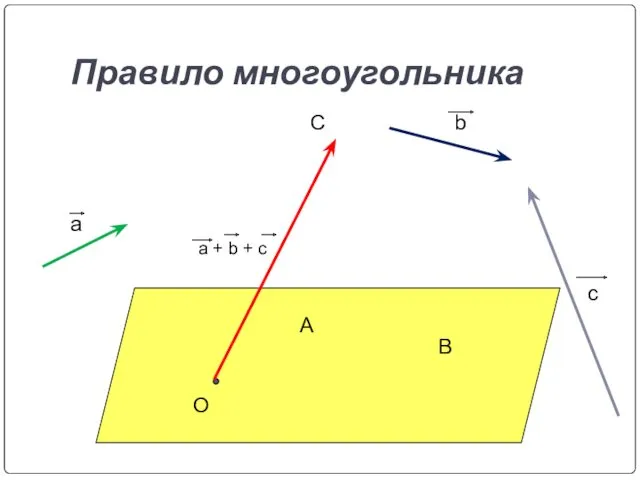
- 14. Правило многоугольника О С В А a b c a + b + c
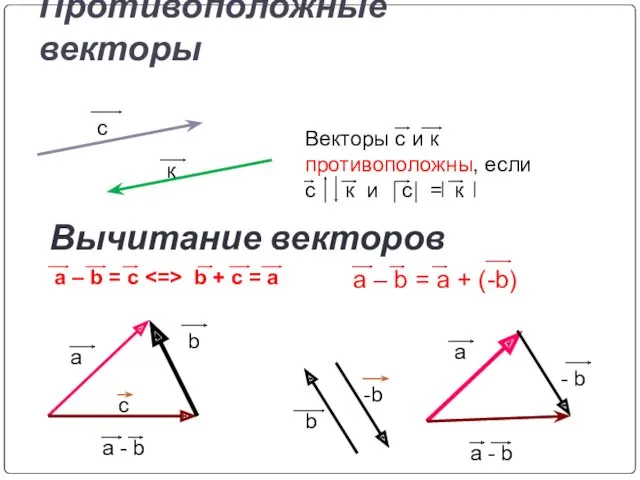
- 15. Противоположные векторы a b a - b - b a a - b с к Векторы
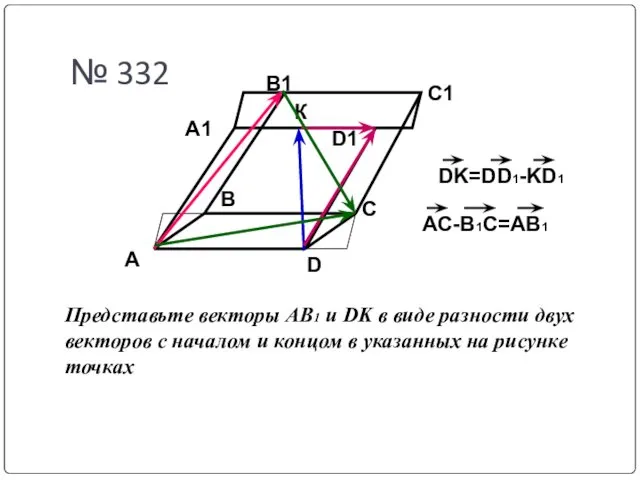
- 16. A D C B A1 B1 C1 D1 № 332 К Представьте векторы АВ1 и DK
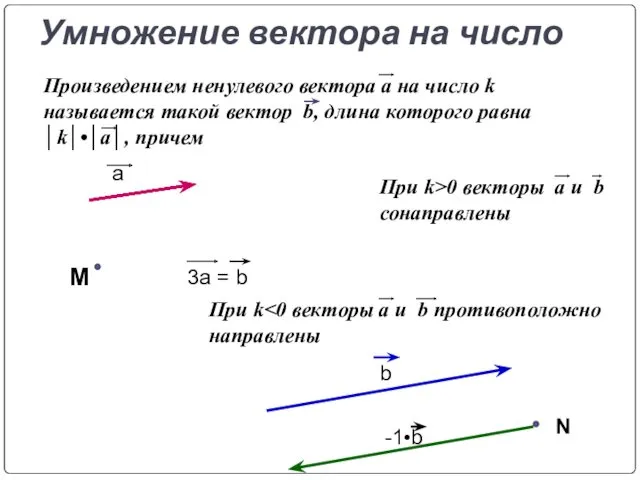
- 17. Умножение вектора на число a 3a = b M b N -1•b Произведением ненулевого вектора а
- 18. Законы сложения и умножения вектора на число а + b = b + а (переместительный) (а
- 19. § 3 КОМПЛАНАРНЫЕ ВЕКТОРЫ
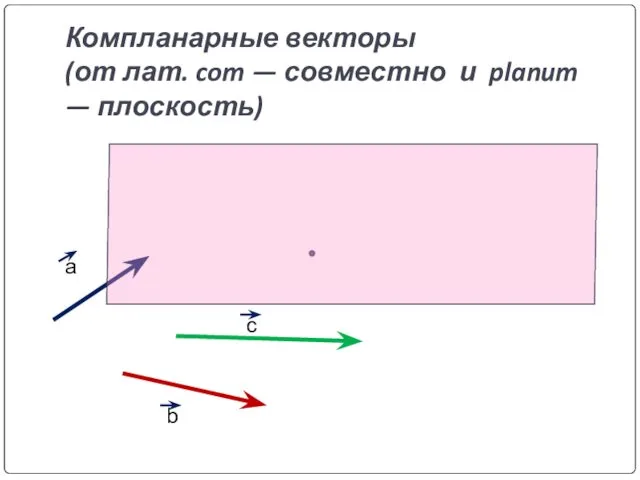
- 20. Компланарные векторы (от лат. com — совместно и planum — плоскость) а b c
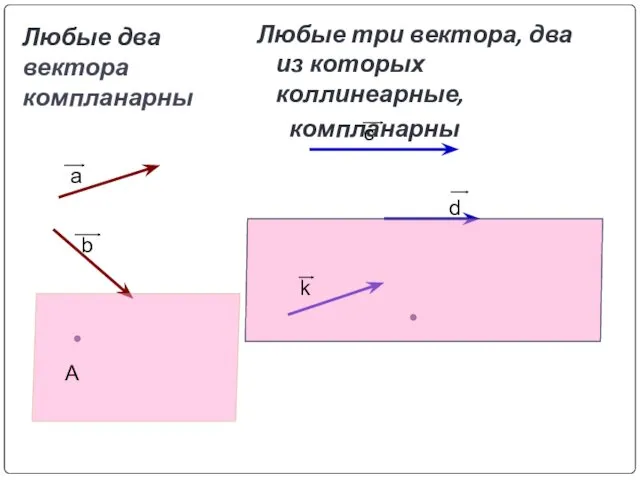
- 21. Любые два вектора компланарны Любые три вектора, два из которых коллинеарные, компланарны A a b c
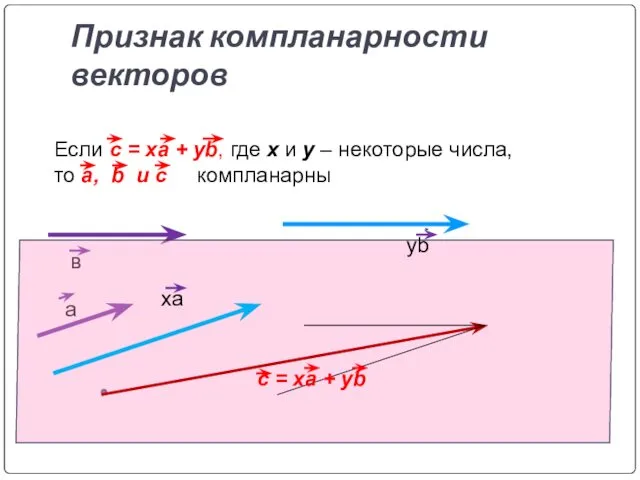
- 22. Признак компланарности векторов Если c = xa + yb, где x и y – некоторые числа,
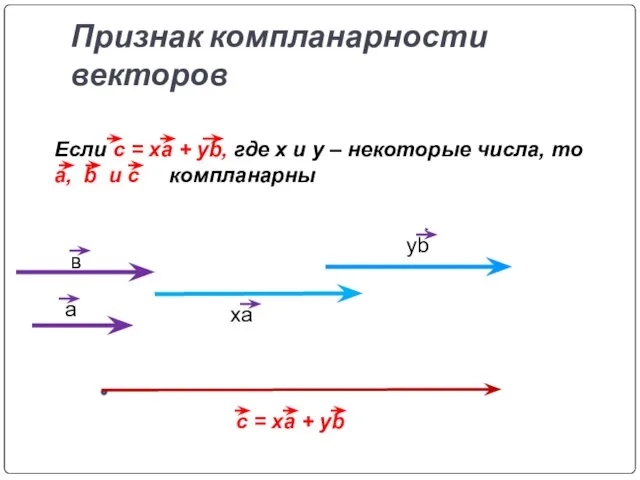
- 23. Признак компланарности векторов Если c = xa + yb, где x и y – некоторые числа,
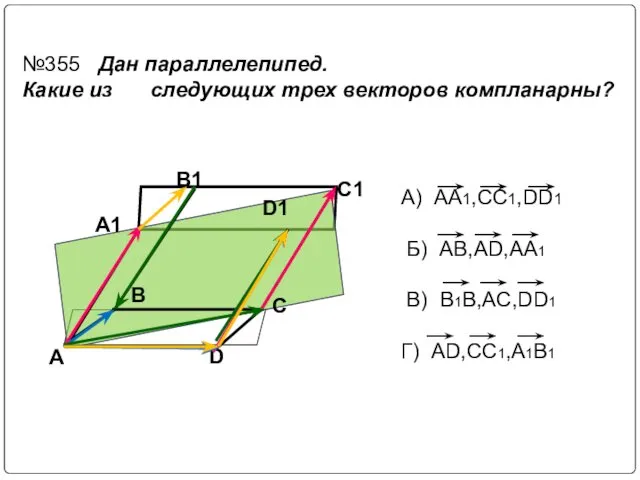
- 24. A D C B A1 B1 C1 D1 №355 Дан параллелепипед. Какие из следующих трех векторов
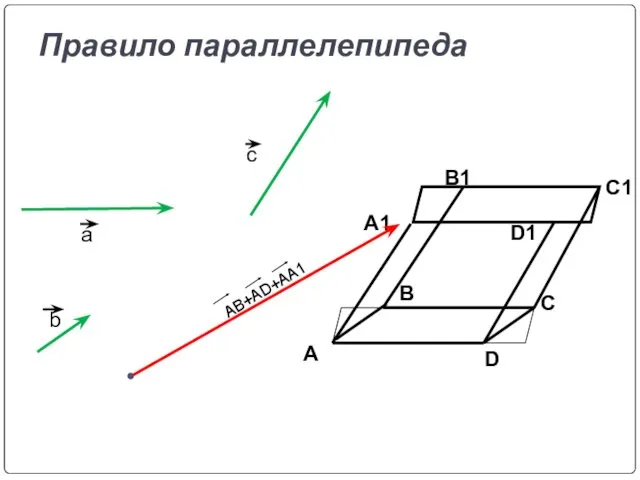
- 25. Правило параллелепипеда A D C B A1 B1 C1 D1 AB+AD+AA1 a b c
- 27. Скачать презентацию




 Площадь треугольника
Площадь треугольника Изготовление развертки
Изготовление развертки Формирование познавательной учебной деятельности на уроках математики с применением технологии развития критического мышления
Формирование познавательной учебной деятельности на уроках математики с применением технологии развития критического мышления Число девять и цифра 9
Число девять и цифра 9 Действительные числа
Действительные числа Задачи по математике
Задачи по математике Введение в математику. Краткие справочно-информационные сведения
Введение в математику. Краткие справочно-информационные сведения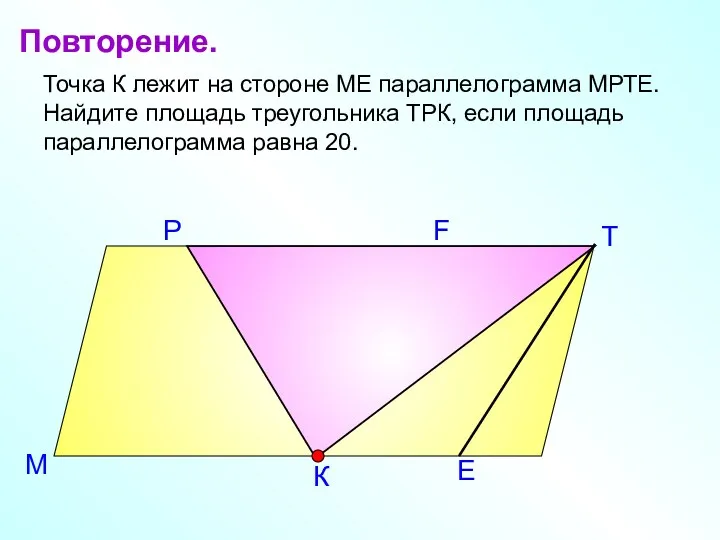 Площадь трапеции
Площадь трапеции Математическая игра Счастливый случай. 5 класс
Математическая игра Счастливый случай. 5 класс Геометрические построения
Геометрические построения Застосування різних способів розкладання многочленів на множники
Застосування різних способів розкладання многочленів на множники Определители: основные понятия
Определители: основные понятия Разложение на простые множители
Разложение на простые множители Решение иррациональных уравнений
Решение иррациональных уравнений Состав чисел первого десятка. Анимированный плакат. 1 класс
Состав чисел первого десятка. Анимированный плакат. 1 класс Нахождение числа по его дроби
Нахождение числа по его дроби Соотношение между сторонами и углами в прямоугольном треугольнике
Соотношение между сторонами и углами в прямоугольном треугольнике Что называется процентом?
Что называется процентом? Раскрытие скобок
Раскрытие скобок День победы. Точные науки в годы ВОВ
День победы. Точные науки в годы ВОВ Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел Поставь правильно знаки Игровое упражнение
Поставь правильно знаки Игровое упражнение презентация Математика (материалы для подготовки будущих первоклассников к школе)
презентация Математика (материалы для подготовки будущих первоклассников к школе)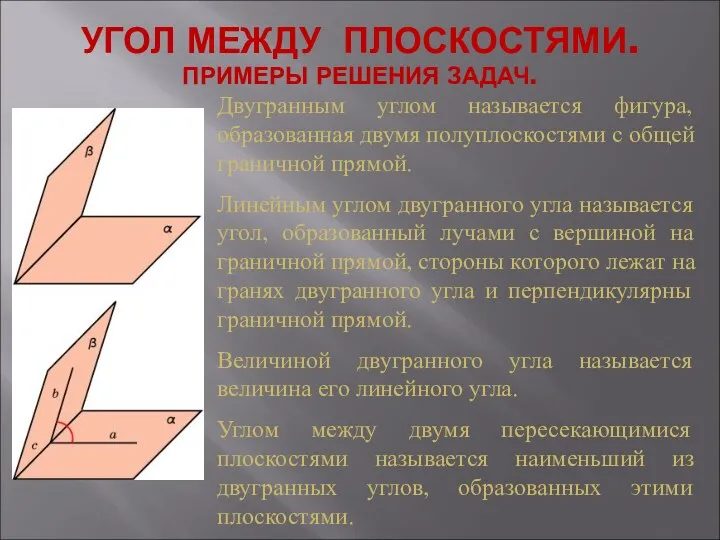 Угол между плоскостями. Примеры решения задач
Угол между плоскостями. Примеры решения задач Осевая и центральная симметрия. Алгоритмы построения фигур
Осевая и центральная симметрия. Алгоритмы построения фигур Табличное сложение
Табличное сложение Случаи вычитания 11-
Случаи вычитания 11- Дополнительные главы линейной алгебры
Дополнительные главы линейной алгебры