Содержание
- 2. Учебные вопросы: Основные понятия Математическая постановка общей задачи линейного программирования (ОЗЛП) Транспортная задача Геометрический метод решения
- 3. Первый учебный вопрос: Основные понятия
- 4. 1. Основные понятия 1.1 Сущность задач оптимального планирования Оптимальное планирование – комплекс методов который позволяет выбрать
- 5. 1.1 Сущность задач оптимального планирования Основные задачи: Правильно и чётко формулировать цели экономической системы в целом
- 6. 1.2 Классификация задач оптимального планирования I. По характеру взаимосвязи между переменными: линейные; нелинейные. II. По характеру
- 7. 1.2 Классификация задач оптимального планирования (продолжение) IV. По наличию информации: полные определённости; неполные информации. V. По
- 8. 1.3 Методы математического проектирования Дифференциальный; Линейный; Нелинейный; Динамический; Стохастический (вероятностный); Эвристический (интуиция, мнение экспертов) и т.д.
- 9. 1.4 Проблемы решаемые методами линейного программирования Оптимальное распределение мощностей различных машин, станков, механизмов; Оптимальное использование транспортных
- 10. Второй учебный вопрос: Математическая постановка общей задачи линейного программирования (ОЗЛП)
- 11. 2.1 Общие математические признаки общей задачи линейного программирования (ОЗЛП) Отыскание экстремума (min; max); Наличие большого числа
- 12. 2.2 Постановка общей задачи Найти значение переменных Х1, Х2, …, Хn, которые обращают в max или
- 13. 2.3 Формы записи задачи линейного программирования Стандартная; Каноническая; Векторная; Матричная.
- 14. Третий учебный вопрос: Транспортная задача
- 15. 3.1 Транспортная задача В зависимости от выбранного критерия эффективности различают следующие задачи: по суммарному пробегу; по
- 16. 3.1 Транспортная задача линейного проектирования (ТЗЛП) в общем виде Исходные данные: Скi - склады с запасом
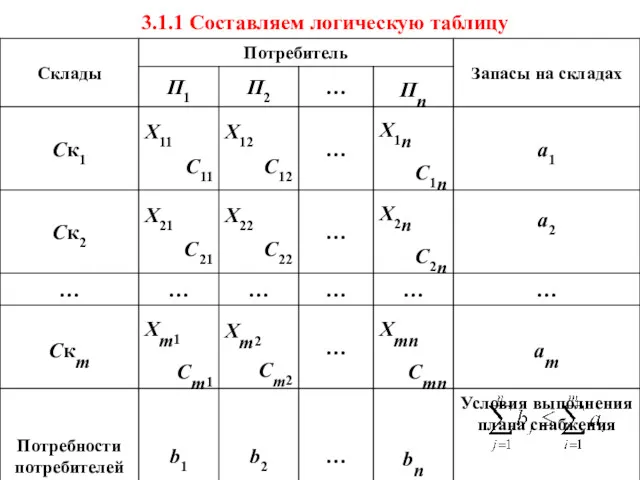
- 17. 3.1.1 Составляем логическую таблицу
- 18. 3.1.2 На основе таблицы составляем целевую функцию Целевая функция Ограничения по запасам на складах Ограничения по
- 19. Четвёртый учебный вопрос: Геометрический метод решения ОЗЛП
- 20. 4.1 Основа метода Задачам линейного программирования можно дать наглядную геометрическую интерпретацию, которая позволяет наглядно увидеть ряд
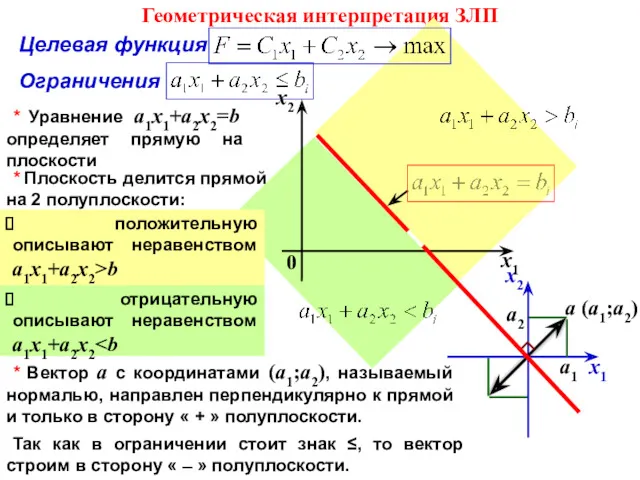
- 21. Целевая функция Ограничения * Плоскость делится прямой на 2 полуплоскости: Геометрическая интерпретация ЗЛП
- 22. Построить на координатной плоскости область соответствующую ограничениям, которые представлены прямыми линиями. Определить положительную или отрицательную полуплоскость
- 23. 5. Определить направление возрастания или убывания целевой функции в зависимости от её вида (min; max) с
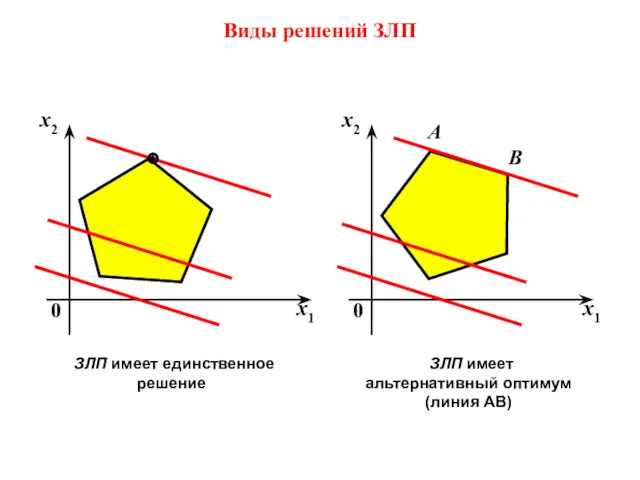
- 24. ЗЛП имеет единственное решение Виды решений ЗЛП ЗЛП имеет альтернативный оптимум (линия АВ)
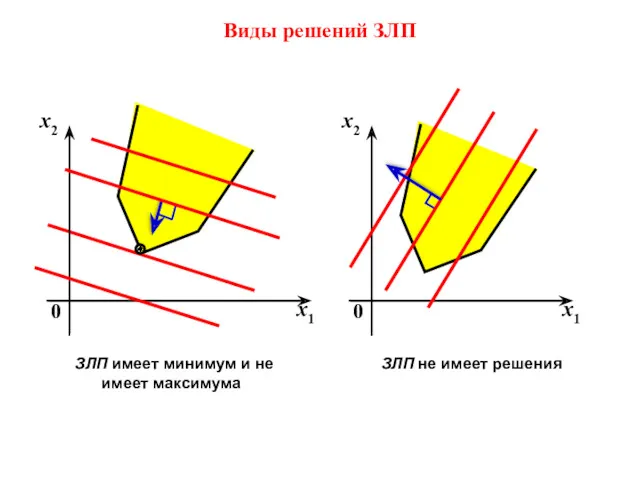
- 25. ЗЛП имеет минимум и не имеет максимума Виды решений ЗЛП ЗЛП не имеет решения
- 26. Пятый учебный вопрос: Пример решения ЗЛП
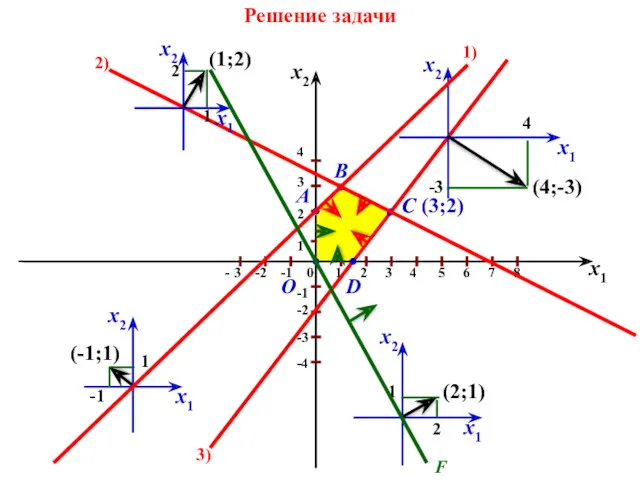
- 27. Целевая функция F = 2х1 + х2 → max Ограничения Решить задачу геометрическим методом Решение задачи
- 28. I Этап: II Этап: Определить направление векторов. III Этап: Выделить ОДР и её вершины – ОАВСД
- 29. V Этап: Определить направление вектора. VI Этап: Перебираем все точки для F = 2х1 + х2
- 30. Решение задачи C (3;2)
- 31. P.S. Если взять целевую функцию F = х1 + 2х2 → max при тех же ограничениях,
- 32. Шестой учебный вопрос: Двойственные задачи линейного программирования
- 33. Двойственность в линейном программировании это принцип, который заключается в том, чтобы для каждой задачи ЛП путём
- 34. 6.1 Основные понятия (продолжение)
- 35. В экономической литературе цены ресурсов y1, y2, …, ym носят следующие названия – учётные, неявные, теневые.
- 36. Алгоритм составления двойственной задачи I. Привести все неравенства системы ограничений прямой задачи к одному смыслу: Если
- 37. II. Составить расширенную матрицу коэффициентов прямой задачи Алгоритм составления двойственной задачи (продолжение)
- 38. III. Составить расширенную матрицу двойственной задачи, транспонированную (замена строк столбцами с сохранением порядка) к прямой Алгоритм
- 39. IV. Сформировать двойственную задачу. Fпр → Fдв , хj → yi; число переменных в двойственной задаче
- 40. Составить задачу двойственную следующей Целевая функция F = - х1 + х2 → max Ограничения Пример
- 41. I. Приведём все неравенства системы ограничений к виду ≤, так как ЦФ → max. С этой
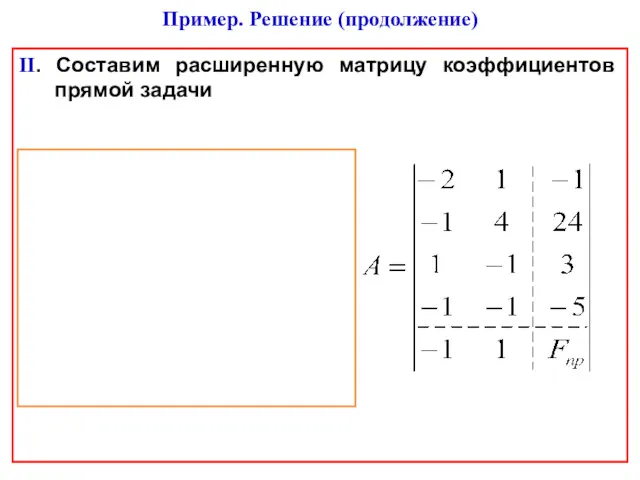
- 42. II. Составим расширенную матрицу коэффициентов прямой задачи Пример. Решение (продолжение)
- 43. III. Составим расширенную матрицу двойственной задачи транспонированную к прямой Пример. Решение (продолжение)
- 44. IV. Сформируем двойственную задачу Целевая функция FДВ = ̶ у1 + 24 у2 + 3у3 ̶
- 46. Скачать презентацию





































 Формула бинома Ньютона. Свойства биномиальных коэффициентов
Формула бинома Ньютона. Свойства биномиальных коэффициентов Устный счет. Сложение с переходом через десяток. Часть 2
Устный счет. Сложение с переходом через десяток. Часть 2 Математика в календаре
Математика в календаре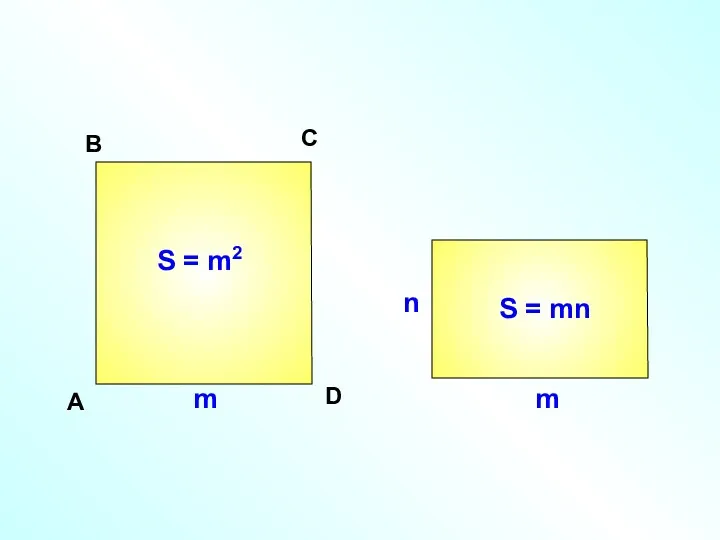 Площади фигур
Площади фигур Предел функции
Предел функции Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов
Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов Умножение круглых чисел
Умножение круглых чисел Цилиндр. Понятие цилиндрической поверхности
Цилиндр. Понятие цилиндрической поверхности Числовые промежутки
Числовые промежутки Анализ эмпирических данных. (Тема 9)
Анализ эмпирических данных. (Тема 9) Функция y=sinx и её график
Функция y=sinx и её график Проблема качества систем автоматического управления. Тема 4
Проблема качества систем автоматического управления. Тема 4 Презентация Больше, меньше 1 класс
Презентация Больше, меньше 1 класс Самостоятельная математическая деятельность детей дошкольного возраста
Самостоятельная математическая деятельность детей дошкольного возраста Первый признак равенства треугольников. (7 класс)
Первый признак равенства треугольников. (7 класс) Знаки тригонометрических функций
Знаки тригонометрических функций Урок математики в 1 классе ( Гармония).
Урок математики в 1 классе ( Гармония). Компоненты суммы
Компоненты суммы Письменное деление многозначных чисел на трехзначное число
Письменное деление многозначных чисел на трехзначное число Урок математики в 4 классе по теме: Прямоугольный параллелепипед. Куб.
Урок математики в 4 классе по теме: Прямоугольный параллелепипед. Куб. Интегральное исчисление функций одной переменной
Интегральное исчисление функций одной переменной Конспект занятия Путешествие по стране логики
Конспект занятия Путешествие по стране логики Перпендикуляр и наклонные Перпендикуляр из точки А к плоскости a
Перпендикуляр и наклонные Перпендикуляр из точки А к плоскости a Математическая игра Звёздный час
Математическая игра Звёздный час Множення десяткових дробів
Множення десяткових дробів Усечённая пирамида
Усечённая пирамида Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс
Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа