Содержание
- 2. Повторение пройденного
- 3. Часть 1 - ГЛАВА 9. ЗАКОН БОЛЬШИХ ЧИСЕЛ. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- 4. При статистическом определении вероятности она трактуется как некоторое число, к которому стремится относительная частота случайного события.
- 5. При увеличении числа испытаний биномиальный закон стремится к нормальному распределению. Это теорема Муавра–Лапласа, которая является частным
- 6. 9.1. Неравенство Чебышева Пусть случайная величина ξ имеет конечные математическое ожидание M[ξ] и дисперсию D[ξ]. Тогда
- 7. Примечания Для противоположного события: Неравенство Чебышева справедливо для любого закона распределения. Положив , получаем нетривиальный факт:
- 8. 9.2. Закон больших чисел в форме Чебышева Теорема Пусть случайные величины попарно независимы и имеют конечные
- 9. 9.2. Закон больших чисел в форме Чебышева: дополнение Теорема (Маркова): закон больших чисел выполняется, если дисперсия
- 10. 9.3. Теорема Бернулли Теорема: Рассмотрим схему Бернулли. Пусть μn – число наступлений события А в n
- 11. Доказательство: Случайная величина μn распределена по биномиальному закону, поэтому имеем
- 12. 9.4. Характеристические функции Характеристической функцией случайной величины называется функция где exp(x) = ex. Таким образом, представляет
- 13. Для непрерывной случайной величины с плотностью распределения вероятности
- 15. 9.5. Центральная предельная теорема (теорема Ляпунова)
- 16. Повторили пройденное
- 17. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ЧАСТЬ II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- 18. Эпиграф «Существует три вида лжи: ложь, наглая ложь и статистика» Бенджамин Дизраэли
- 19. Введение Две основные задачи математической статистики: сбор и группировка статистических данных; разработка методов анализа полученных данных
- 20. Методы статистического анализа данных: оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров известного распределения;
- 21. ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- 22. 1.1. Генеральная совокупность и выборка Генеральная совокупность - все множество исследуемых объектов, Выборка – набор объектов,
- 23. Выборка бывает повторной, когда каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность, и бесповторной,
- 24. Репрезентативная выборка: правильно представляет особенности генеральной совокупности, т.е. является репрезентативной (представительной). По закону больших чисел, можно
- 25. Генеральная совокупность и выборка могут быть одномерными (однофакторными) и многомерными (многофакторными)
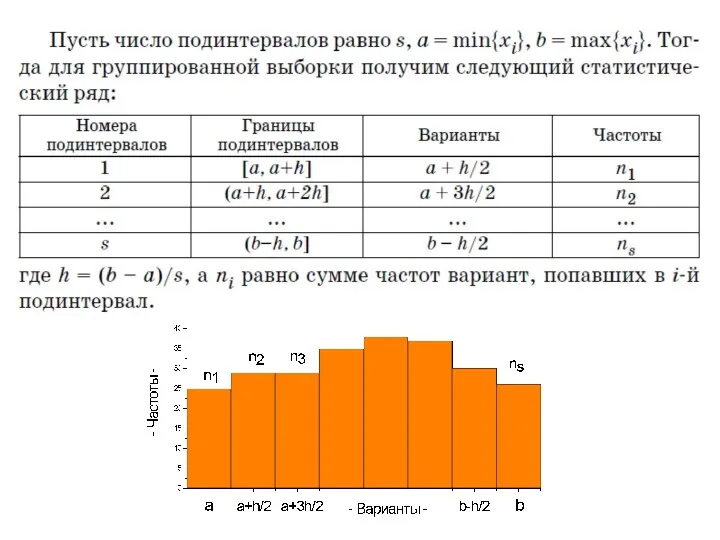
- 26. 1.2. Выборочный закон распределения (статистический ряд) Пусть в выборке объемом n интересующая нас случайная величина ξ
- 27. Разность xmax – xmin есть размах выборки, отношение ωi = ni /n – относительная частота варианты
- 28. Если мы запишем варианты в возраста-ющем порядке, то получим вариацион-ный ряд. Таблица, состоящая из таких упорядоченных
- 29. Если вариационный ряд состоит из очень большого количества чисел или исследуется некоторый непрерывный признак, используют группированную
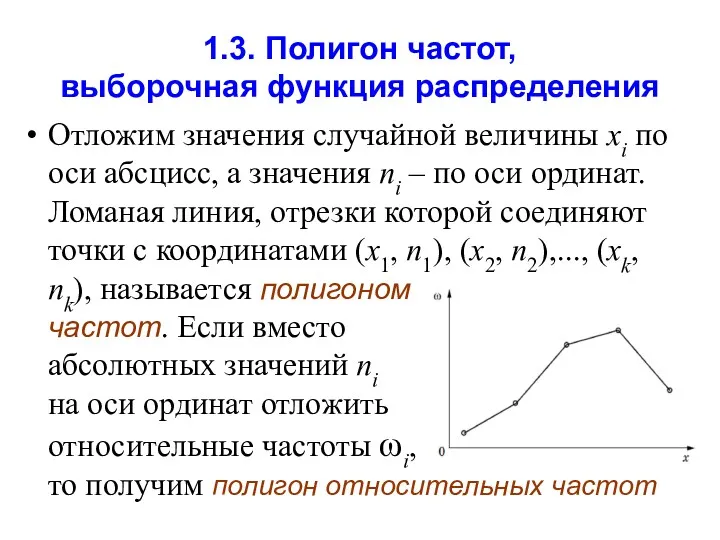
- 31. 1.3. Полигон частот, выборочная функция распределения Отложим значения случайной величины xi по оси абсцисс, а значения
- 32. По аналогии с функцией распределения дискретной случайной величины по выборочному закону распределения можно построить выборочную (эмпирическую)
- 33. В отличие от функции ,найденной для случайной величины ξ опытным путем в результате обработки статис-тических данных,
- 34. Заметим, что:
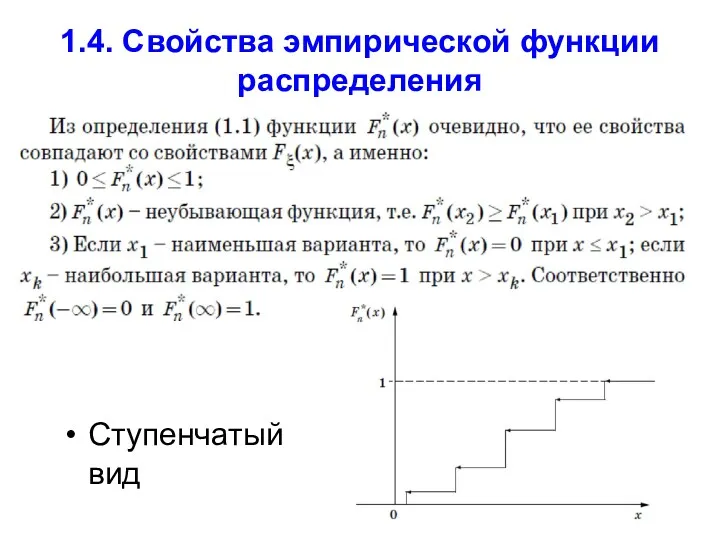
- 35. 1.4. Свойства эмпирической функции распределения Ступенчатый вид
- 36. Еще одним графическим представлением интересующей нас выборки является гистограмма – ступенчатая фигура, состоящая из прямоугольников, основани-ями
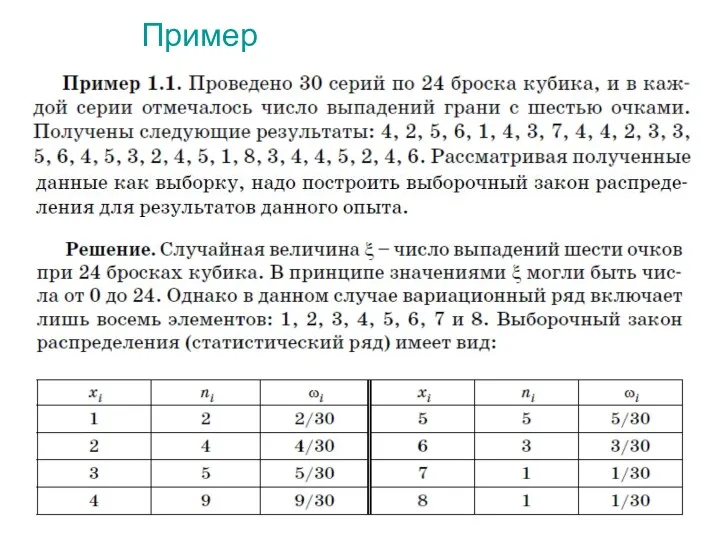
- 37. Пример
- 38. ГЛАВА 2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ
- 39. Задача математической статистики – по имеющейся выборке получить информацию о генеральной совокупности. Числовые характерис-тики репрезентативной выборки
- 40. 2.1. Выборочное среднее и выборочная дисперсия, эмпирические моменты Выборочным средним называется среднее арифметическое значений вариант в
- 41. Выборочной дисперсией называется величина, равная Выборочным средним квадратическим отклонением –
- 42. Легко показать, что выполняется следующее соотношение, удобное для вычисления дисперсии:
- 43. Другими характеристиками вариационного ряда являются: мода M0 – варианта, имеющая наибольшую частоту, и медиана me –
- 44. По аналогии с соответствующими теоретическими выражениями можно построить эмпирические моменты, применяемые для статистической оценки начальных и
- 45. По аналогии с моментами теории вероятностей начальным эмпирическим моментом порядка m называется величина центральным эмпирическим моментом
- 46. 2.2. Свойства статистических оценок параметров распределения: несмещен-ность, эффективность, состоятельность После получения статистических оценок параметров распределения случайной
- 48. Статистическая оценка A* называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности A при
- 49. Разброс отдельных значений относительно среднего значения M[A*] зависит от величины дисперсии D[A*]. Если дисперсия велика, то
- 50. К статистическим оценкам предъявляется еще требование состоятельности. Оценка называется состоятельной, если при n → она стремится
- 51. 2.3. Свойства выборочного среднего Будем полагать, что варианты x1, x2,..., xn являются значениями соответствующих независимых одинаково
- 52. Несмещенность. Из свойств математического ожидания следует, что т.е. выборочное среднее является несмещенной оценкой математического ожидания случайной
- 53. Состоятельность. Пусть a – оцениваемый параметр, а именно математическое ожидание генеральной совокупности – дисперсия генеральной совокупности
- 54. Таким образом, можно сделать вывод, что выборочное среднее является несмещенной, эффективной (по крайней мере, для нормального
- 56. ЛЕКЦИЯ 6
- 57. 2.4. Свойства выборочной дисперсии Исследуем несмещенность выборочной дисперсии D* как оценки дисперсии случайной величины
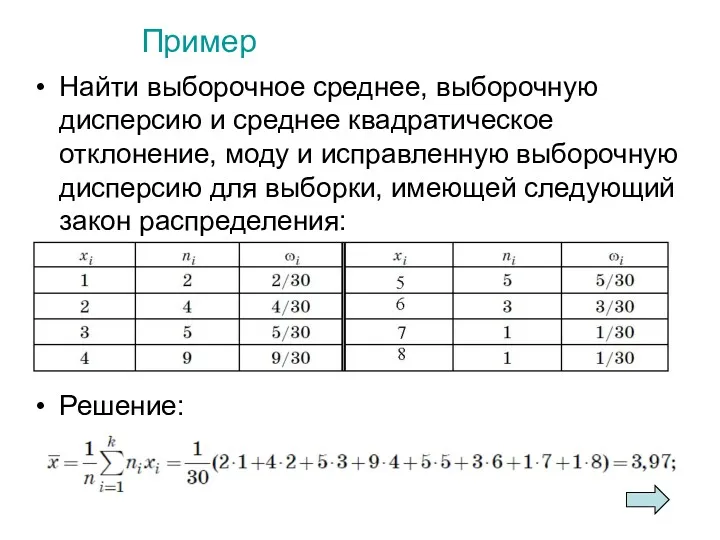
- 60. Пример Найти выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение, моду и исправленную выборочную дисперсию для
- 62. ГЛАВА 3. ТОЧЕЧНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ ИЗВЕСТНОГО РАСПРЕДЕЛЕНИЯ
- 63. Будем считать, что общий вид закона распределения нам известен и остается уточнить детали – параметры, определяющие
- 64. 3.1. Метод моментов
- 65. Метод моментов, развитый Карлом Пирсоном в 1894 г., основан на использовании этих приближенных равенств: моменты рассчитываются
- 66. Можно показать, что оценки параметров θ, полученные методом моментов, состоятельны, их математические ожидания отличаются от истинных
- 67. Пример Известно, что характеристика ξ объектов генеральной совокупности, являясь случайной величиной, имеет равномерное распределе-ние, зависящее от
- 68. Напоминание α1 – мат.ожидание β2 - дисперсия
- 69. (*)
- 71. 3.2. Метод наибольшего правдоподобия В основе метода лежит функция правдоподобия L(x1, x2,..., xn, θ), являющаяся законом
- 72. Идея метода наибольшего правдоподобия состоит в том, что мы ищем такие значения параметров θ, при которых
- 73. Оценки по методу максимального правдоподобия получаются из необходимого условия экстремума функции L(x1,x2,..., xn,θ) в точке
- 74. Примечания: 1. При поиске максимума функции правдоподобия для упрощения расчетов можно выполнить действия, не изменяющие результата:
- 75. Пример Решение. В данной задаче следует оценить два неизвестных параметра: a и σ2. Логарифмическая функция правдоподобия
- 76. Отбросив в этой формуле слагаемое, которое не зависит от a и σ2, составим систему уравнений правдоподобия
- 77. ГЛАВА 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ ИЗВЕСТНОГО РАСПРЕДЕЛЕНИЯ
- 78. Задачу оценивания параметра известного распределения можно решать путем построения интервала, в который с заданной вероятностью попадает
- 79. (*)
- 80. 4.1. Оценивание математического ожидания нормально распределенной величины при известной дисперсии Пусть исследуемая случайная величина ξ распре-делена
- 81. Имеем: (1) (2)
- 82. (*) (*) (2) (1)
- 83. 4.2. Оценивание математического ожидания нормально распределенной величины при неизвестной дисперсии
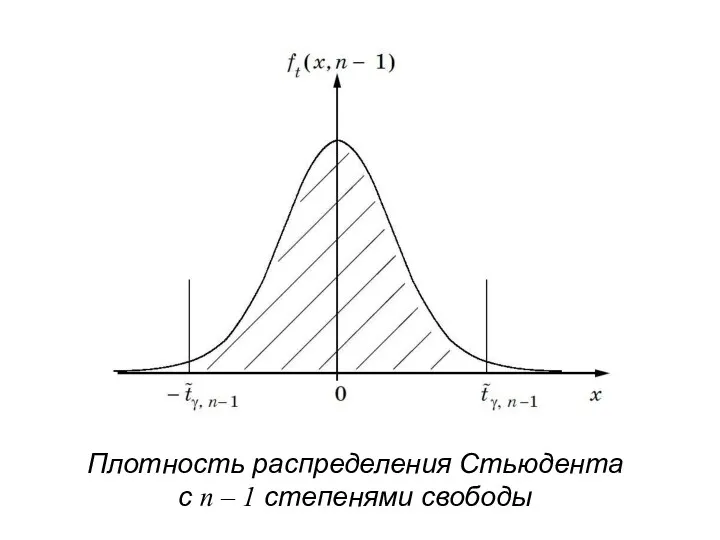
- 84. Известно, что случайная величина tn, заданная таким образом, имеет распределение Стьюдента с k = n –
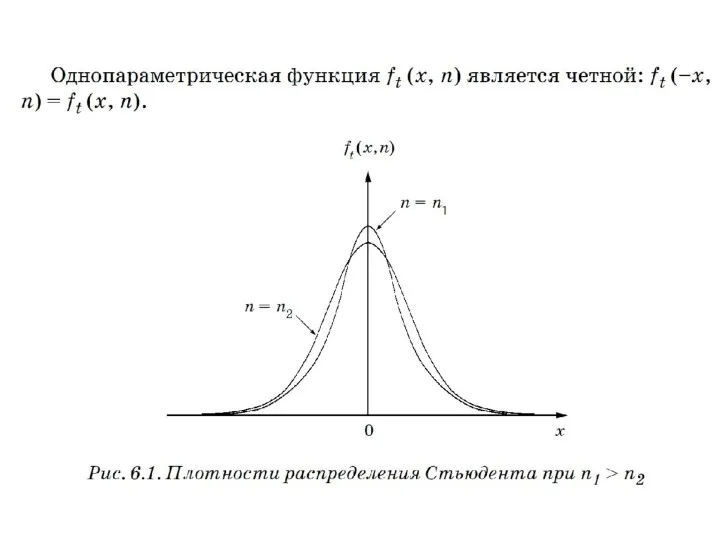
- 86. Плотность распределения Стьюдента c n – 1 степенями свободы
- 89. Примечание. При большом числе степеней свободы k распределение Стьюдента стремится к нормальному распределению с нулевым математическим
- 90. 4.3. Оценивание среднего квадратического отклонения нормально распределенной величины Пусть исследуемая случайная величина ξ распределена по нормальному
- 91. 4.3.1. Частный случай известного математического ожидания Пусть известно значение M[ξ] = a и требуется оценить только
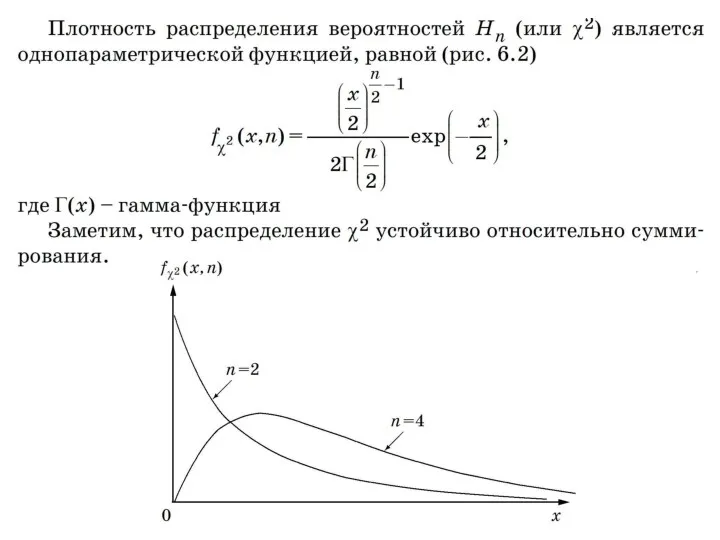
- 92. Рассмотрим случайную величину Стоящие под знаком суммы случайные величины имеют нормальное распределение с плотностью fN (x,
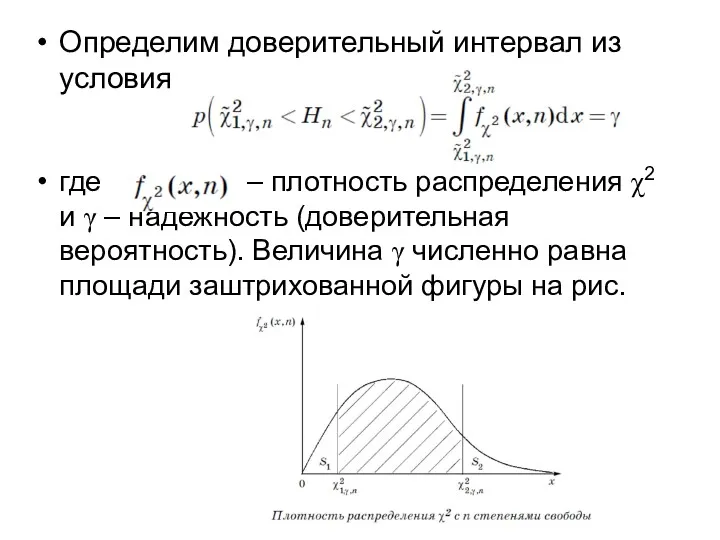
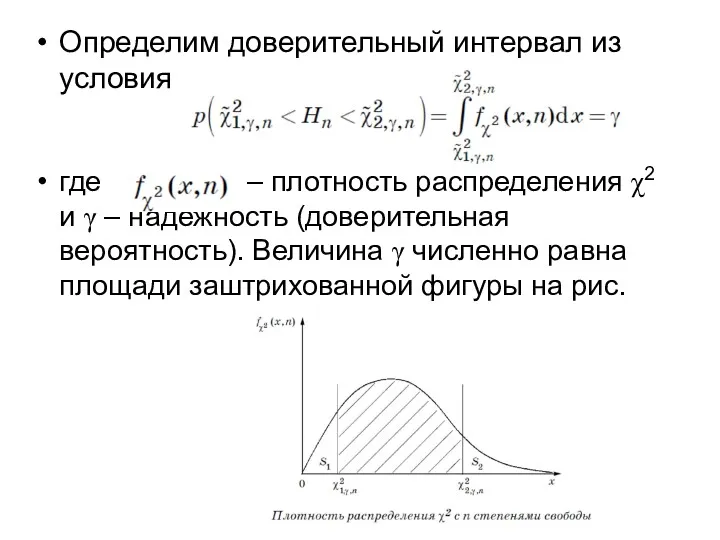
- 93. Определим доверительный интервал из условия где – плотность распределения χ2 и γ – надежность (доверительная вероятность).
- 97. 4.3.2. Частный случай неизвестного математического ожидания На практике чаще всего встречается ситуация, когда неизвестны оба параметра
- 99. 4.4. Оценивание математического ожидания случайной величины для произвольной выборки Интервальные оценки математического ожидания M[ξ], полученные для
- 100. Как и выше, будем рассматривать варианты x1, x2,..., xn как значения независимых, одинаково распределенных случайных величин
- 101. Поэтому, если известно значение дисперсии случайной величины ξ, то можно пользоваться приближенными формулами Если же значение
- 103. Лекция 7
- 104. Повторение пройденного
- 105. ГЛАВА 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ ИЗВЕСТНОГО РАСПРЕДЕЛЕНИЯ
- 106. Задачу оценивания параметра известного распределения можно решать путем построения интервала, в который с заданной вероятностью попадает
- 107. (*)
- 108. 4.1. Оценивание математического ожидания нормально распределенной величины при известной дисперсии Пусть исследуемая случайная величина ξ распре-делена
- 109. Имеем: (1) (2)
- 110. (*) (*) (2) (1)
- 111. 4.2. Оценивание математического ожидания нормально распределенной величины при неизвестной дисперсии
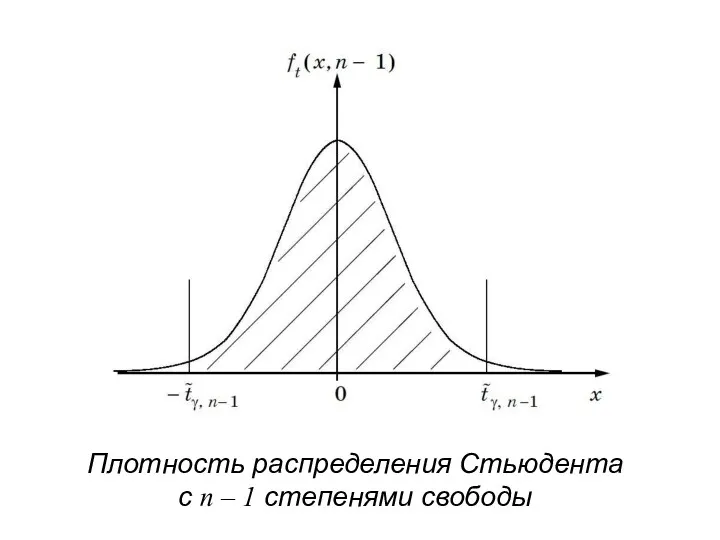
- 112. Известно, что случайная величина tn, заданная таким образом, имеет распределение Стьюдента с k = n –
- 114. Плотность распределения Стьюдента c n – 1 степенями свободы
- 117. Примечание. При большом числе степеней свободы k распределение Стьюдента стремится к нормальному распределению с нулевым математическим
- 118. 4.3. Оценивание среднего квадратического отклонения нормально распределенной величины Пусть исследуемая случайная величина ξ распределена по нормальному
- 119. 4.3.1. Частный случай известного математического ожидания Пусть известно значение M[ξ] = a и требуется оценить только
- 120. Рассмотрим случайную величину Стоящие под знаком суммы случайные величины имеют нормальное распределение с плотностью fN (x,
- 121. Определим доверительный интервал из условия где – плотность распределения χ2 и γ – надежность (доверительная вероятность).
- 125. 4.3.2. Частный случай неизвестного математического ожидания На практике чаще всего встречается ситуация, когда неизвестны оба параметра
- 127. 4.4. Оценивание математического ожидания случайной величины для произвольной выборки Интервальные оценки математического ожидания M[ξ], полученные для
- 128. Как и выше, будем рассматривать варианты x1, x2,..., xn как значения независимых, одинаково распределенных случайных величин
- 129. Поэтому, если известно значение дисперсии случайной величины ξ, то можно пользоваться приближенными формулами Если же значение
- 130. Повторили пройденное
- 131. ГЛАВА 5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
- 132. Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известного распределения случайной величины. Проверяемая
- 133. Вероятность ошибки первого рода будем называть уровнем значимости и обозначать как α. Основной прием проверки статистических
- 135. 5.1. Проверка гипотез о параметрах известного распределения 5.1.1. Проверка гипотезы о математическом ожидании нормально распределенной случайной
- 136. В случае известной дисперсии D[ξ] = σ2, как и в п. 4.1, определим случайную величину ,
- 143. 5.1.2. Сравнение дисперсий нормально распределенных случайных величин Пусть имеются две нормально распределенные случайные величины Для них
- 144. Учитывая несмещенность исправленных выборочных дисперсий, нулевую гипотезу можно записать следующим образом: где случайная величина принимает значения
- 145. Случайная величина F имеет распределение Фишера – Снедекора с числом степеней свободы k1 = n1 –
- 148. 5.1.3. Сравнение математических ожиданий независимых случайных величин Сначала рассмотрим случай нормального распределения случайных величин с известными
- 149. Введем случайные величины , принимающие значения выборочных средних соответственно. Поскольку выборочные средние – это несмещенные оценки
- 153. 5.2. Проверка гипотез о виде закона распределения случайной величины. Критерий Пирсона Надежное предположение о распределении случайной
- 154. Известно несколько критериев согласия. Достоинством критерия Пирсона является его универсальность. С его помощью можно проверять гипотезы
- 155. 5.2.1. Проверка гипотезы о нормальном распределении Пусть имеется случайная величина ξ и сделана выборка достаточно большого
- 159. ГЛАВА 6. ВАЖНЕЙШИЕ РАСПРЕДЕЛЕНИЯ И ИХ КВАНТИЛИ
- 160. 6.1. Нормальное распределение По определению нормально распределенная случайная величина ξ имеет плотность распределения вероятностей где a
- 161. Квантилью порядка α (0 Квантиль x½ называется медианой случайной величины ξ, квантили x¼ и x¾ –
- 162. 6.2. Распределение Стьюдента Если – независимые случайные величины, имеющие нормальное распределение с нулевым математическим ожиданием и
- 167. 6.3. Распределение χ2 Если ξ1, ξ2, …, ξn – независимые случайные величины, имеющие нормальное распределение с
- 172. ГЛАВА 7. ПРИМЕР СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ВЫБОРКИ
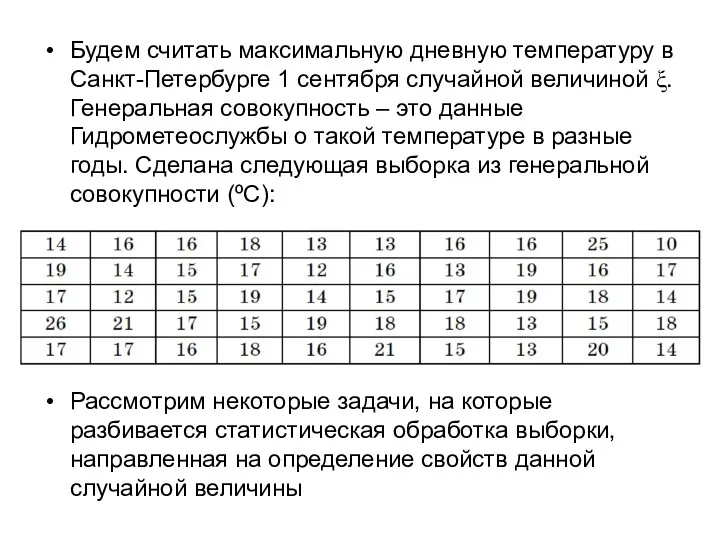
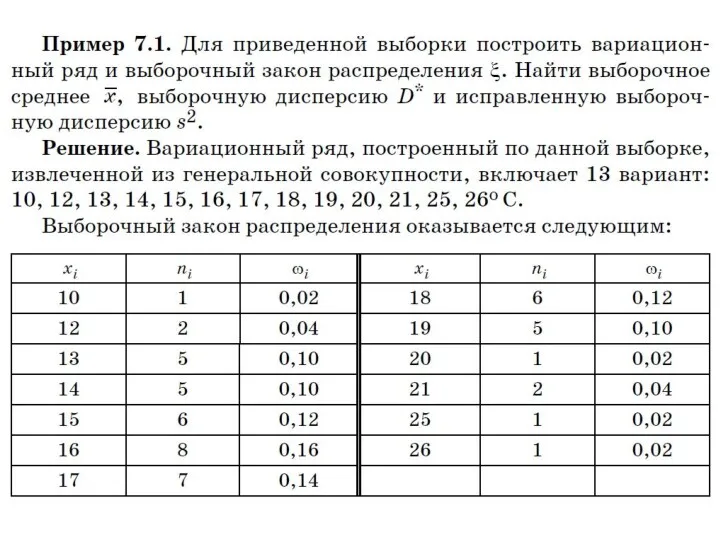
- 173. Будем считать максимальную дневную температуру в Санкт-Петербурге 1 сентября случайной величиной ξ. Генеральная совокупность – это
- 180. Скачать презентацию











































![Разброс отдельных значений относительно среднего значения M[A*] зависит от величины](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/284866/slide-48.jpg)







































![4.3.1. Частный случай известного математического ожидания Пусть известно значение M[ξ]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/284866/slide-90.jpg)

























![4.3.1. Частный случай известного математического ожидания Пусть известно значение M[ξ]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/284866/slide-118.jpg)















![В случае известной дисперсии D[ξ] = σ2, как и в](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/284866/slide-135.jpg)






































 Урок математики
Урок математики Решение задач на готовых чертежах. Вводное повторение. Геометрия. 9 класс
Решение задач на готовых чертежах. Вводное повторение. Геометрия. 9 класс Grafika komputerowa
Grafika komputerowa Математическое странствие
Математическое странствие Перевод обыкновенной дроби в десятичную
Перевод обыкновенной дроби в десятичную Презентация КВН по математике
Презентация КВН по математике Lemke’s Algorithm: The Hammer in Your Math Toolbox?
Lemke’s Algorithm: The Hammer in Your Math Toolbox? Решение линейных неравенств
Решение линейных неравенств Методы и приемы решения уравнений с параметром
Методы и приемы решения уравнений с параметром Десятичные дроби
Десятичные дроби Лекция 2 ЦОС. Преобразование речевых сигналов к цифровому виду
Лекция 2 ЦОС. Преобразование речевых сигналов к цифровому виду Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Вычитание из чисел 6 и 7. Состав чисел 6 и 7
Вычитание из чисел 6 и 7. Состав чисел 6 и 7 Правило сложения отрицательных чисел
Правило сложения отрицательных чисел Решение задач на нахождение дроби от числа
Решение задач на нахождение дроби от числа Знакомство с задачей.
Знакомство с задачей. Теорема Пифагора. Применение теоремы в ходе решения задач
Теорема Пифагора. Применение теоремы в ходе решения задач Презентация:Открытое занятие по ФЭМП в средней группе
Презентация:Открытое занятие по ФЭМП в средней группе Определенный интеграл: основные понятия
Определенный интеграл: основные понятия Презентация Геометрические фигуры
Презентация Геометрические фигуры Позначення чисел другого десятка цифрами. Вимірювання довжини
Позначення чисел другого десятка цифрами. Вимірювання довжини Площадь и периметр прямоугольника
Площадь и периметр прямоугольника Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость. Задания
Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость. Задания Десятичная запись дробных чисел (повторение)
Десятичная запись дробных чисел (повторение) Состав чисел первого десятка
Состав чисел первого десятка Среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия. Урок 3. 10 класс
Среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия. Урок 3. 10 класс Сложение однозначных чисел с переходом через десяток
Сложение однозначных чисел с переходом через десяток Методы кибернетики
Методы кибернетики