Содержание
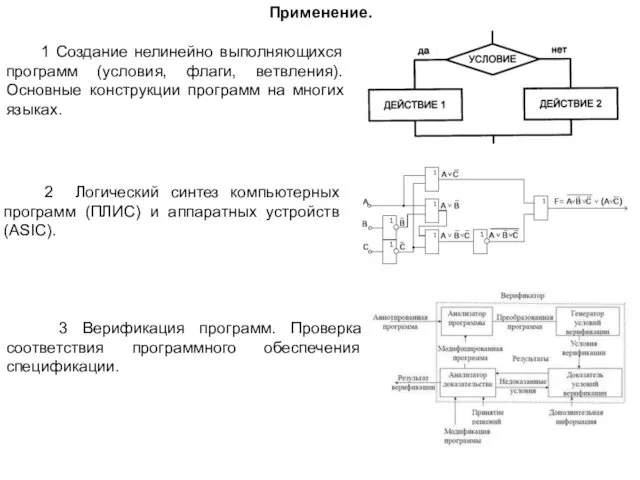
- 2. Применение. 1 Создание нелинейно выполняющихся программ (условия, флаги, ветвления). Основные конструкции программ на многих языках. 2
- 3. Исчисление высказываний – это аксиоматическая логическая система, интерпретацией которой является алгебра высказываний. Алфавит исчисления высказываний состоит
- 4. Формулу Q = F(Х1, Х2, ..., Хn) называют логической функцией, если логическая переменная Q принимает значения
- 5. 2. Тавтологиями - истинными на всех наборах значений атомов из I. Тавтологии представляют собой схемы построения
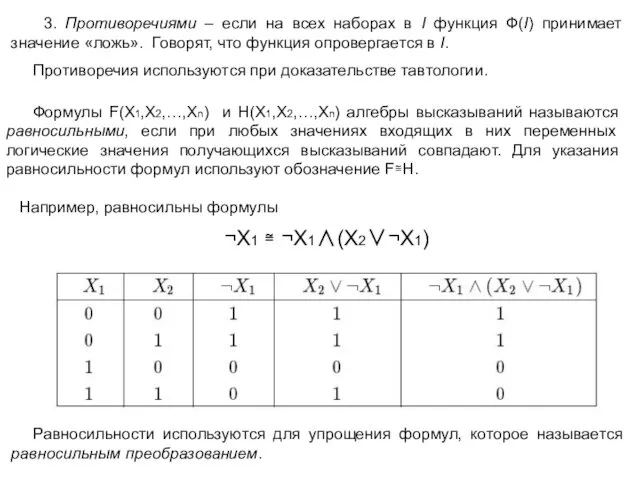
- 6. 3. Противоречиями – если на всех наборах в I функция Ф(I) принимает значение «ложь». Говорят, что
- 7. Основные равносильности, используемые при преобразованиях:
- 8. Нормальные формы высказываний Для каждой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую только отрицание,
- 9. Конъюнктивным одночленом от переменных X1,X2,…,Xn называется конъюнкция этих переменных или их отрицаний, т.е. может входить и
- 10. Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов, т.е. выражение вида K1∨K2∨…∨Kp, где все Ki, i=1,2,…,p, являются
- 11. Алгоритм построения ДНФ 1) Избавиться от всех логических операций, кроме конъюнкций, дизъюнкций, отрицания. Это можно сделать,
- 12. Алгоритм построения КНФ 1) Избавиться от всех логических операций, кроме конъюнкций, дизъюнкций, отрицания. Это можно сделать,
- 13. CДНФ Совершенная дизъюнктивная нормальная форма (СДНФ) – это ДНФ, которая удовлетворяет трём условиям: – в ней
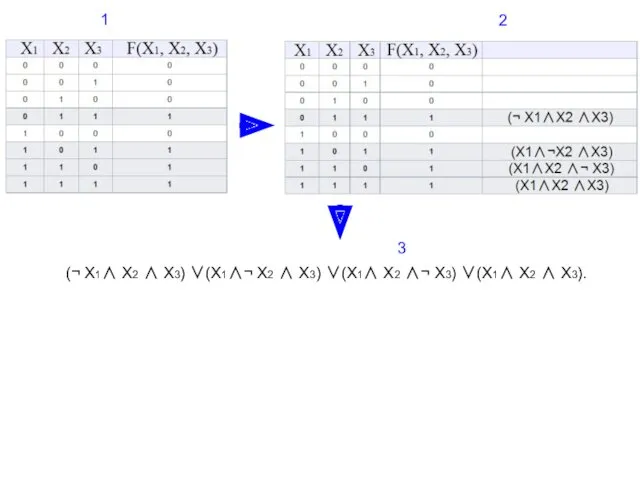
- 14. 1 2 (¬ X1∧ X2 ∧ X3) ∨(X1∧¬ X2 ∧ X3) ∨(X1∧ X2 ∧¬ X3) ∨(X1∧
- 15. CКНФ Совершенная конъюнктивная нормальная форма (СКНФ) – это КНФ, которая удовлетворяет трём условиям: – в ней
- 17. Скачать презентацию










 Презентация_Селяева А.Д
Презентация_Селяева А.Д Презентация посвящённая 100-летию Г.В.Свиридова МБДОУ №25
Презентация посвящённая 100-летию Г.В.Свиридова МБДОУ №25 Важные изменения в законодательстве в 2019 году
Важные изменения в законодательстве в 2019 году Семья субъект социокультурной среды
Семья субъект социокультурной среды презентация по работе семейного клуба Счастливый ребёнок МКДОУ детский сад№4 Золотой петушок. с.Пригородное Ивановская область
презентация по работе семейного клуба Счастливый ребёнок МКДОУ детский сад№4 Золотой петушок. с.Пригородное Ивановская область Презентация 8 класс Рациональное использование природных ресурсов
Презентация 8 класс Рациональное использование природных ресурсов командная игра огонь - наш друг, огонь - наш враг
командная игра огонь - наш друг, огонь - наш враг Представление чисел в формате с плавающей запятой
Представление чисел в формате с плавающей запятой Газопламенное напыление
Газопламенное напыление Шагает эра космоса вперёд.
Шагает эра космоса вперёд. Алтайский заповедник
Алтайский заповедник Профотбор. Проблема отбора
Профотбор. Проблема отбора РобоПлатформа. Старт 2.0 Урок 10
РобоПлатформа. Старт 2.0 Урок 10 Отработка предлагаемых продаж и навыки презентации меню/
Отработка предлагаемых продаж и навыки презентации меню/ ВОИН о ВОЙНЕ работа посвящается Героям Отечества
ВОИН о ВОЙНЕ работа посвящается Героям Отечества 97 А класс әмбебап тігін машинасы
97 А класс әмбебап тігін машинасы Презентация Механические волны.
Презентация Механические волны. Презентация к уроку истории и культуры Санкт-Петербурга в 8 классе Памятники воинской славы в Санкт-Петербурге: Отечественная война 1812 года
Презентация к уроку истории и культуры Санкт-Петербурга в 8 классе Памятники воинской славы в Санкт-Петербурге: Отечественная война 1812 года Будова і технічне обслуговування транспортного засобу категорії В. Трансмісія, підвіска та механізми керування
Будова і технічне обслуговування транспортного засобу категорії В. Трансмісія, підвіска та механізми керування Рисуем пасхальные яйца
Рисуем пасхальные яйца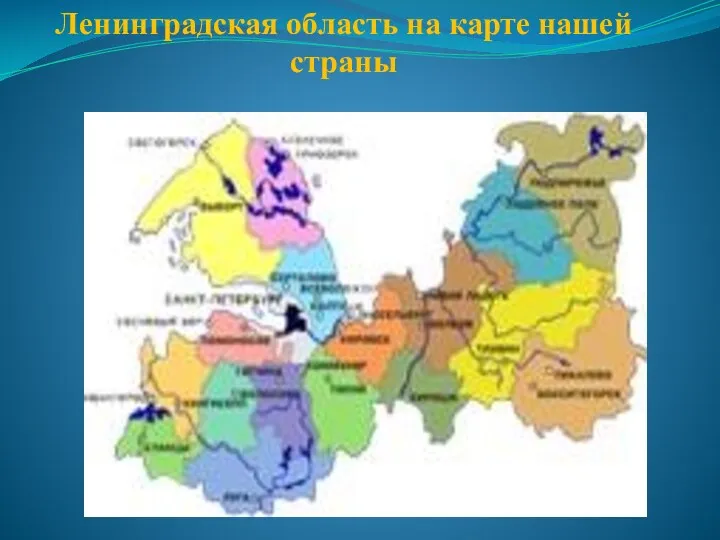 Ленинградская область на карте нашей страны
Ленинградская область на карте нашей страны Петровские преобразования: предпосылки, основные направления, результаты
Петровские преобразования: предпосылки, основные направления, результаты Заболачивание
Заболачивание Моя презентация
Моя презентация Метод щелевой разгрузки пласта в призабойной зоне скважин
Метод щелевой разгрузки пласта в призабойной зоне скважин Система входных приемных устройств 35ВВ РЛС 35Н6
Система входных приемных устройств 35ВВ РЛС 35Н6 Против неограниченной свободы
Против неограниченной свободы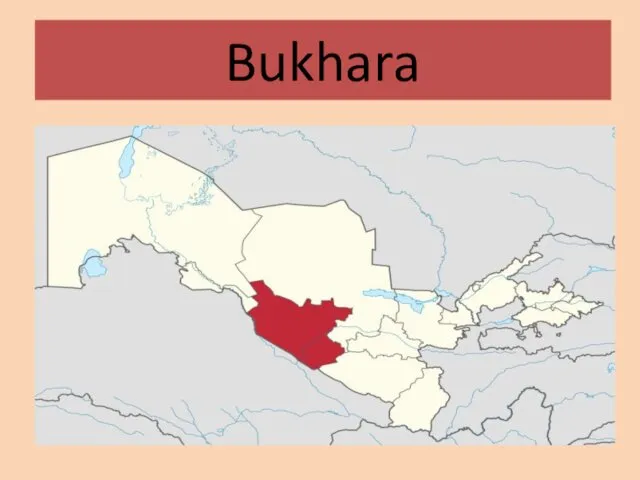 Bukhara
Bukhara