Содержание
- 2. 8.1 Прямая на плоскости 8.1.1. Некоторые понятия Декартова прямоугольная система координат Прямая линия L на плоскости
- 3. Пусть n = (A, B) = Ai + Bj, q = (l, m) = li +
- 4. Уравнение прямой, проходящей через точку M0(x0;y0), перпендикулярно вектору нормали 8.1.2. Общее уравнение прямой на плоскости O(0,
- 5. То же самое для координат: Частные случаи: A = 0, B ≠ 0, C ≠ 0
- 6. a и b – отрезки, отсекаемые прямой на осях Ox и Oy. 8.1.3. Уравнение прямой в
- 7. Пусть прямая ℓ не проходит через O(0;0). cosα·x + cosβ·y + C = 0, 8.1.4. Нормальное
- 8. Уравнение прямой, проходящей через точку M0(x0;y0), параллельно направляющему вектору 8.1.5. Каноническое уравнение прямой Частные случаи: -
- 9. 8.1.6. Уравнение прямой, проходящей через две точки Подставляем в каноническое уравнение: Следствие: условие того, что три
- 10. 8.1.7. Параметрические уравнения прямой Векторное параметрическое уравнение прямой: Найдём это уравнение в декартовых координатах из канонического
- 11. 8.1.8. Уравнение прямой с угловым коэффициентом Частные случаи: если φ = 0, то к = 0
- 12. 8.1.9. Взаимное расположение прямых на плоскости либо параллельны, либо пересекаются. ℓ1: A1x + B1y + C1
- 13. Прямые перпендикулярны, если: (3) k1k2 = -1. Угол между прямыми:
- 14. 8.1.10. Расстояние от точки до прямой Пусть прямая ℓ задана уравнением Ax + By + C
- 15. 8.1.11. Уравнение прямой, проходящей через точку Дано: фиксированная точка прямой M0(x0, y0). 1. Пусть задан вектор
- 16. Пример на нахождение других уравнений прямой Дано: общее уравнение 3x - 4y - 12 = 0
- 17. Пример на нахождение угла между прямыми Дано: прямая 2x + y - 1 = 0 Найти:
- 18. Ещё пример на нахождение угла между прямыми Дано: прямая L1 отсекает на координатных осях отрезки (2;
- 19. Пример на нахождение уравнения прямой, проходящей через точку Дано: точка M(4; -1), прямая 4x + 3y
- 21. Скачать презентацию


















 Материалы, применяемые для изготовления горных инструментов. ТИПИ. Тема 1
Материалы, применяемые для изготовления горных инструментов. ТИПИ. Тема 1 Информационные технологии в профессии. Сфера IT
Информационные технологии в профессии. Сфера IT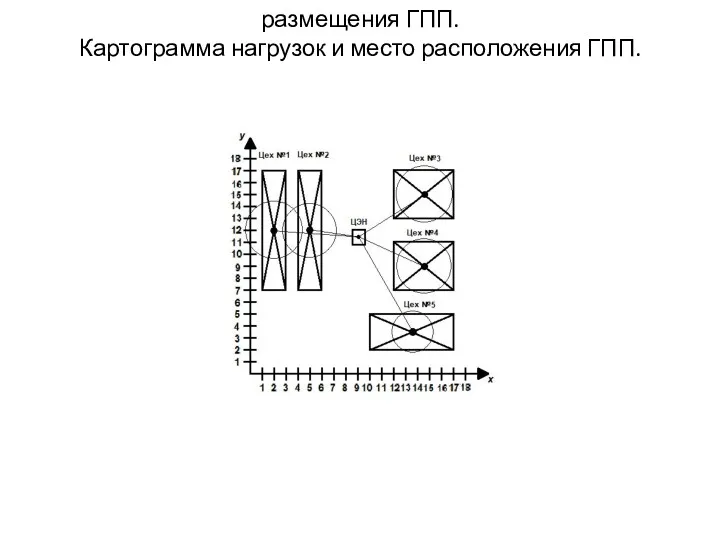 Размещения ГПП. Картограмма нагрузок и место расположения ГПП
Размещения ГПП. Картограмма нагрузок и место расположения ГПП организация и проведение прогулки в детском саду
организация и проведение прогулки в детском саду Что такое музыка. Тест
Что такое музыка. Тест Газетница для хранения газет и журналов
Газетница для хранения газет и журналов Наполняем ваш каталог качественными описаниями товаров
Наполняем ваш каталог качественными описаниями товаров Методическое объединение.
Методическое объединение. Гуманитарные проблемы информационной безопасности
Гуманитарные проблемы информационной безопасности Святая блаженная Матрона Московская
Святая блаженная Матрона Московская Презентация Прогулка по Москве
Презентация Прогулка по Москве Domino Effect Analysis and Assessment of Industrial Sites: A Review of Methodologies and Software Tools
Domino Effect Analysis and Assessment of Industrial Sites: A Review of Methodologies and Software Tools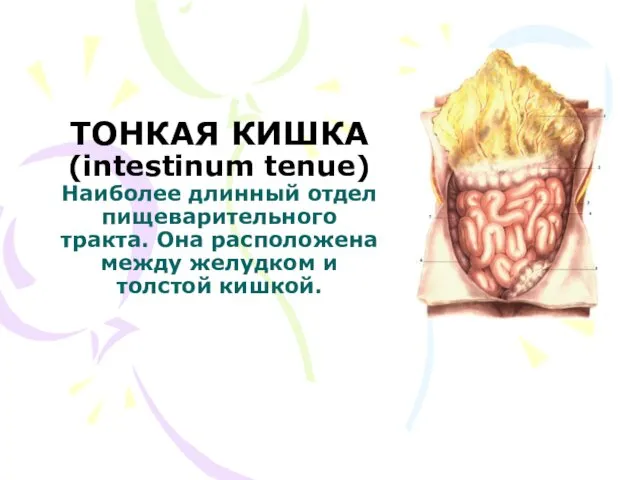 Тонкая кишка. Длина тонкой кишки у человека
Тонкая кишка. Длина тонкой кишки у человека Введение в фармакологию. Основы фармакокинетики
Введение в фармакологию. Основы фармакокинетики Презентация Праздники разных стран мира
Презентация Праздники разных стран мира Опыты с веществами
Опыты с веществами Скажи нет терроризму
Скажи нет терроризму Соединения деталей
Соединения деталей Поделка оригами Зайчик
Поделка оригами Зайчик Устройства электропитания УЭП-МПК
Устройства электропитания УЭП-МПК Что же такое Qlean?
Что же такое Qlean? Газобалонное оборудование второго поколения на СНГ и СПГ
Газобалонное оборудование второго поколения на СНГ и СПГ футбол роботов
футбол роботов Алгоритм Беллмана – Форда
Алгоритм Беллмана – Форда Теория вероятностей. Решение заданий №4
Теория вероятностей. Решение заданий №4 Взаимодествие детей и воспитателя в образовательной области Социально- коммуникативное развитие
Взаимодествие детей и воспитателя в образовательной области Социально- коммуникативное развитие Физические методы в стоматологии
Физические методы в стоматологии Массовое применение кабелей с изоляцией СПЭ в странах Европы и США
Массовое применение кабелей с изоляцией СПЭ в странах Европы и США