Слайд 2

Постановка задачи:
вычислить интеграл вида
где a и b – пределы интегрирования;
f(x)
– непрерывная функция на отрезке [a,b]
Слайд 3
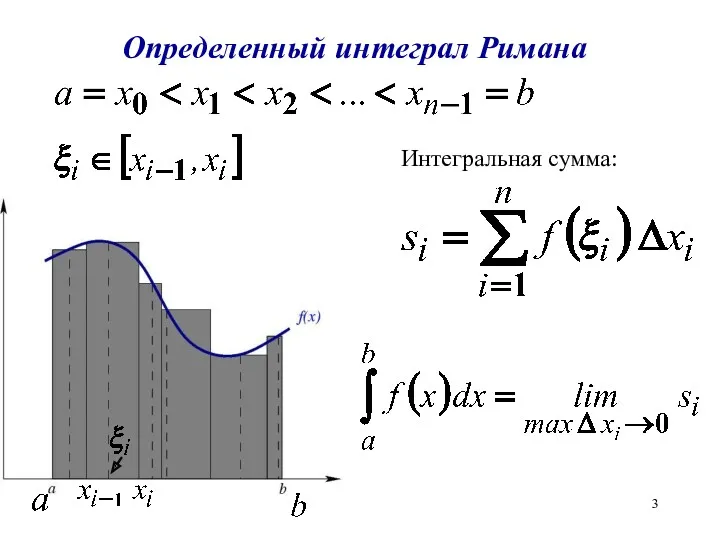
Определенный интеграл Римана
Слайд 4

Вычисление определенных интегралов
Значение определенного интеграла можно трактовать как площадь криволинейной трапеции
Слайд 5

методы численного интегрирования применяют
Если:
1) вид функции f(x) не допускает непосредственного
интегрирования;
2) значения функции f(x) заданы в виде таблицы
Основная идея - замена подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически.
Слайд 6

Квадратурные формулы
Ньютона-Котеса
Замена f(x) – на полином различных степеней.
f(x)=const
- метод прямоугольников,
f(x)=kx+b - метод трапеций,
f(x)=ax2+bx+c - метод Симпсона.
Слайд 7
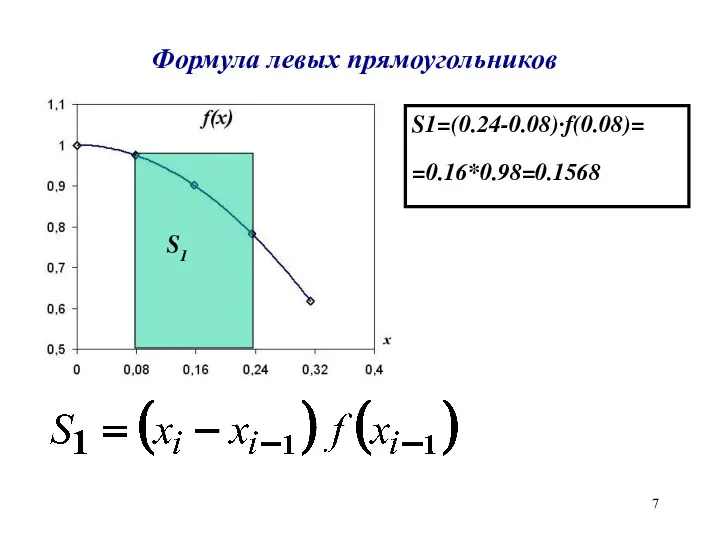
Формула левых прямоугольников
S1
S1=(0.24-0.08)·f(0.08)=
=0.16*0.98=0.1568
Слайд 8
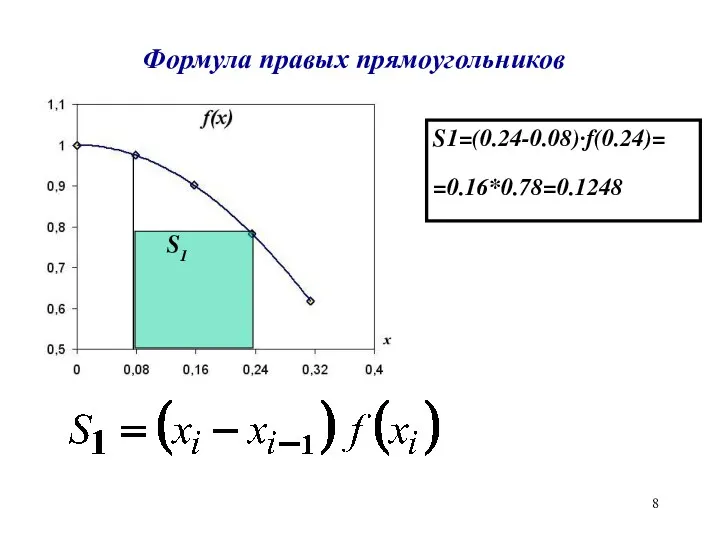
Формула правых прямоугольников
S1
S1=(0.24-0.08)·f(0.24)=
=0.16*0.78=0.1248
Слайд 9
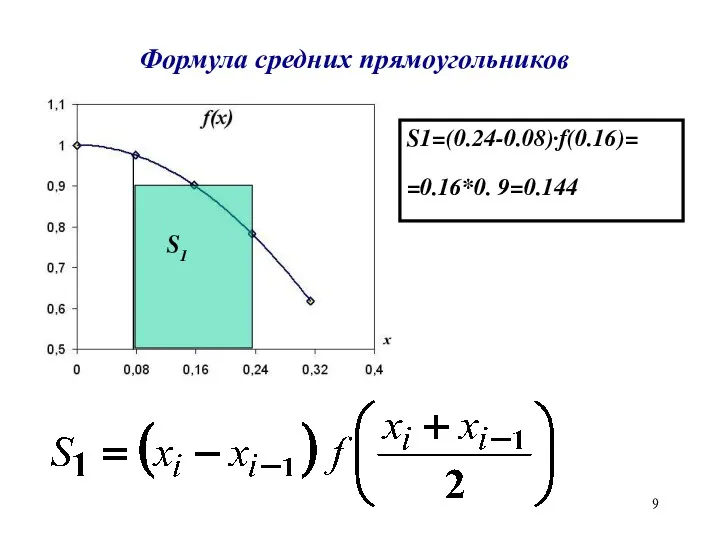
Формула средних прямоугольников
S1
S1=(0.24-0.08)·f(0.16)=
=0.16*0. 9=0.144
Слайд 10
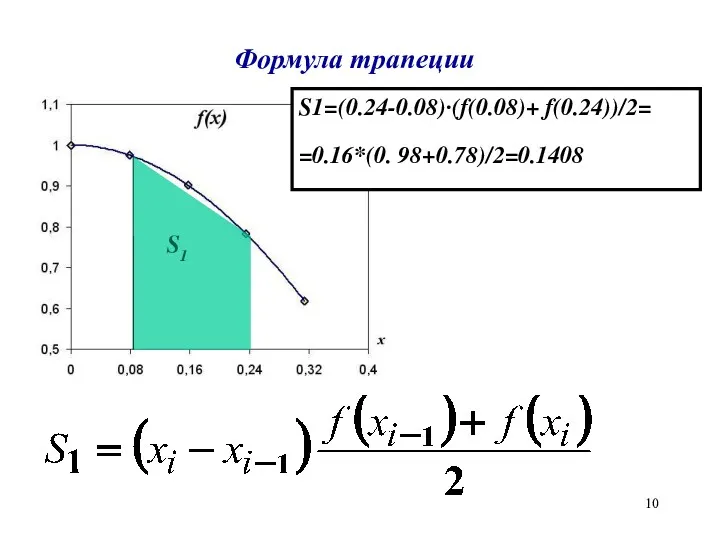
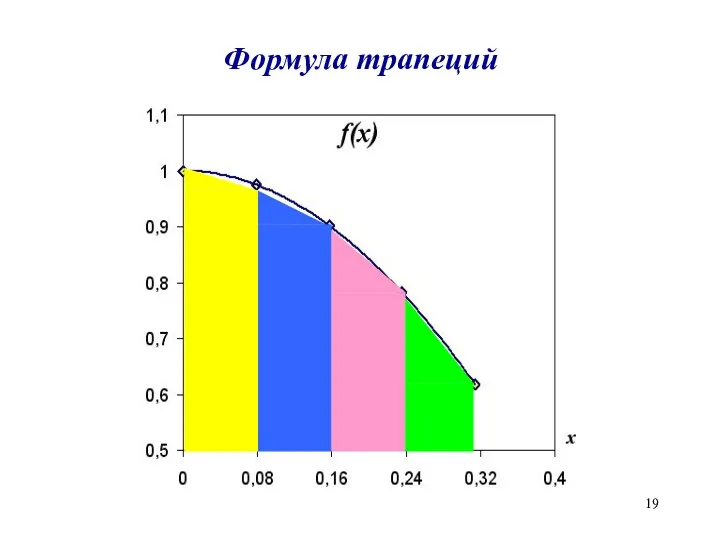
Формула трапеции
S1
S1=(0.24-0.08)·(f(0.08)+ f(0.24))/2=
=0.16*(0. 98+0.78)/2=0.1408
Слайд 11
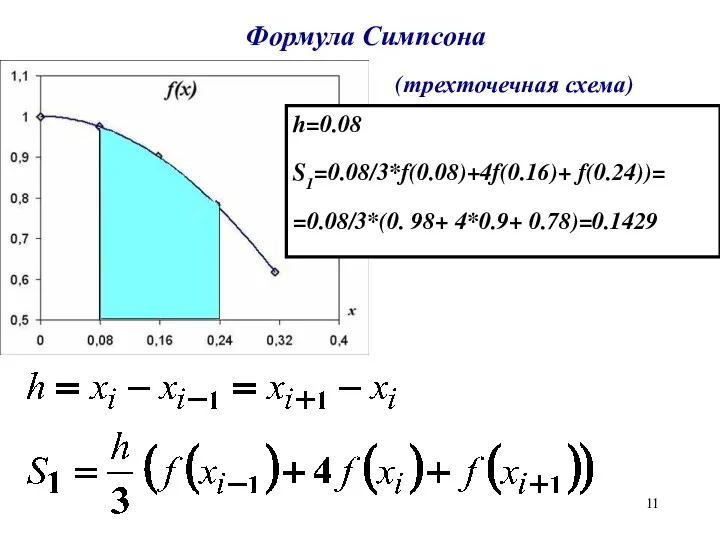
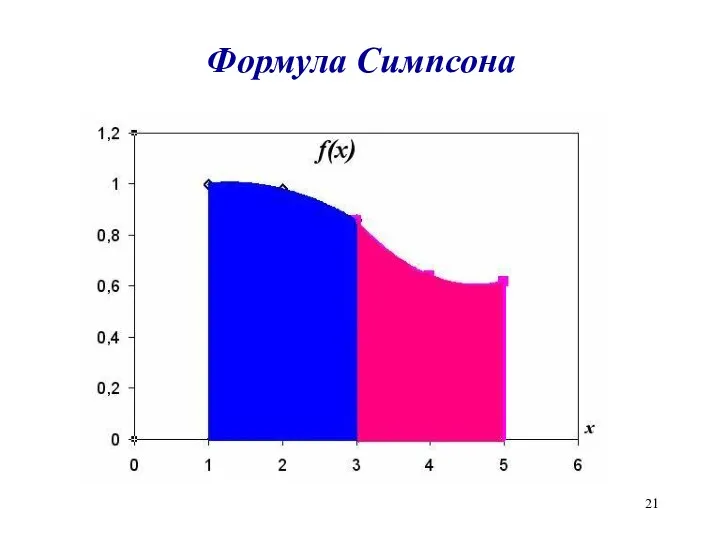
Формула Симпсона
(трехточечная схема)
h=0.08
S1=0.08/3*f(0.08)+4f(0.16)+ f(0.24))=
=0.08/3*(0. 98+ 4*0.9+ 0.78)=0.1429
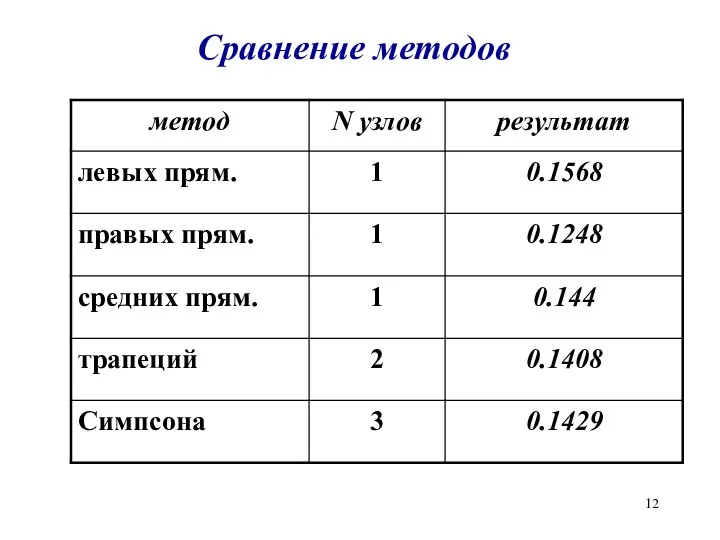
Слайд 12
Слайд 13
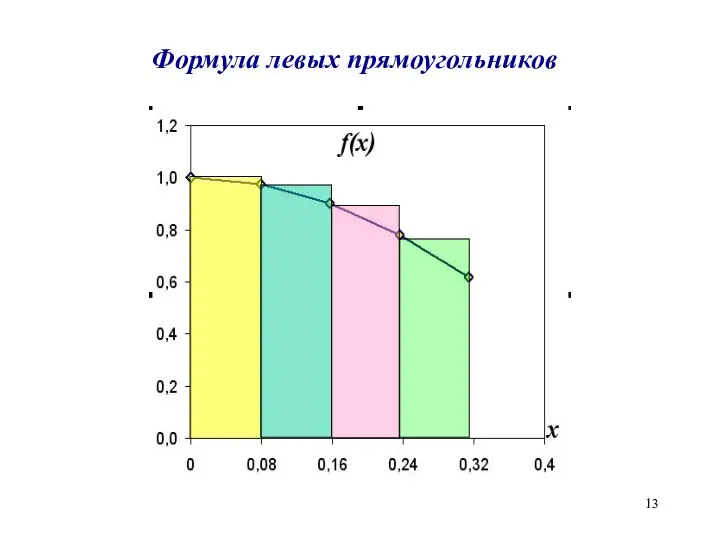
Формула левых прямоугольников
Слайд 14

Метод левых прямоугольников
n – количество отрезков
Слайд 15
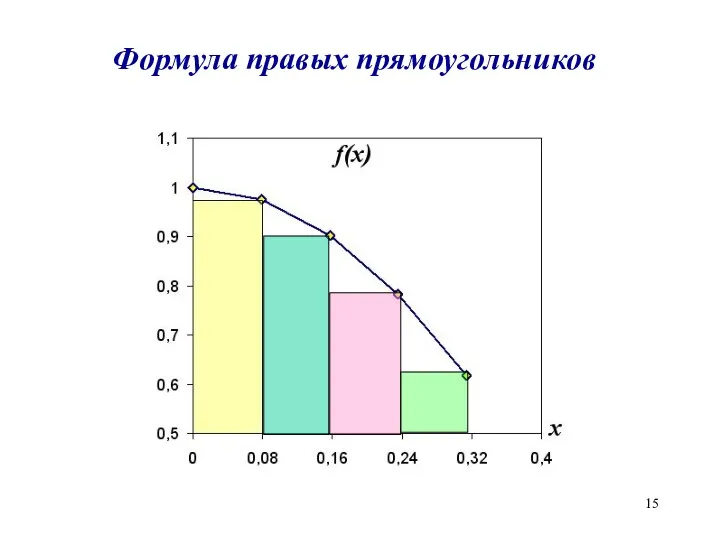
Формула правых прямоугольников
Слайд 16

Метод правых прямоугольников
Слайд 17
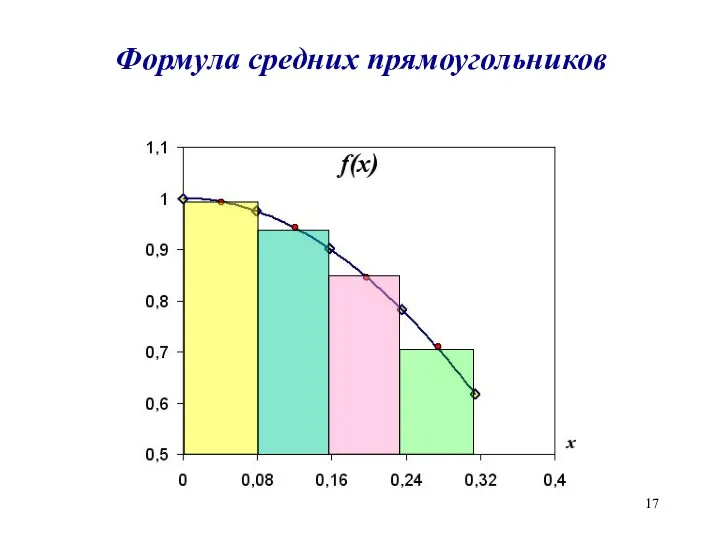
Формула средних прямоугольников
Слайд 18

Метод средних прямоугольников
n – количество отрезков
Слайд 19
Слайд 20

Слайд 21
Слайд 22

Слайд 23
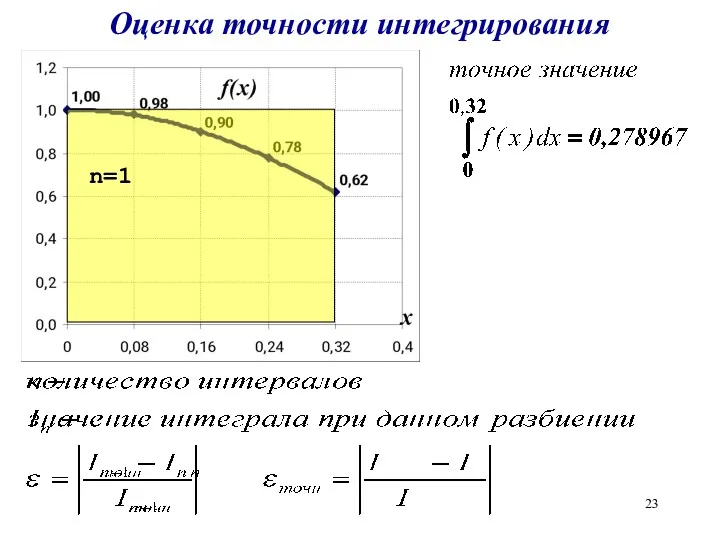
Оценка точности интегрирования
Слайд 24
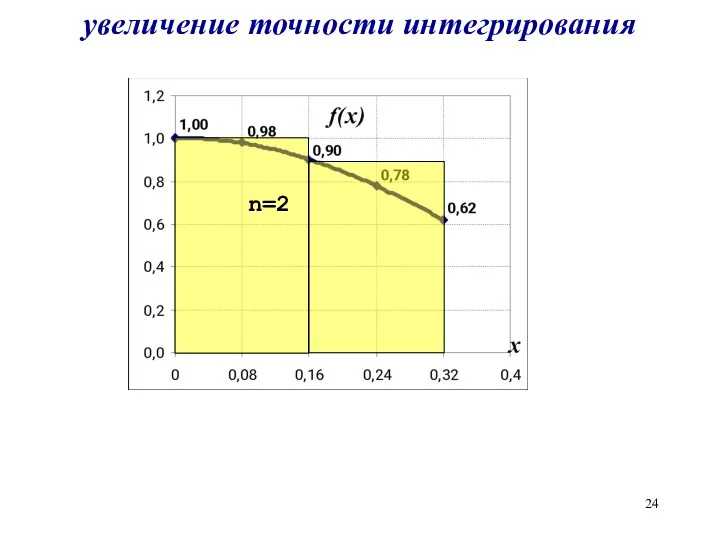
увеличение точности интегрирования
Слайд 25
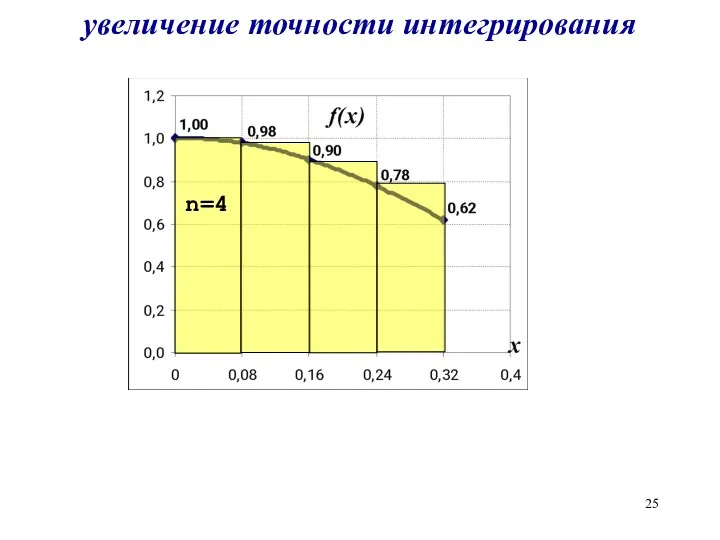
увеличение точности интегрирования
Слайд 26
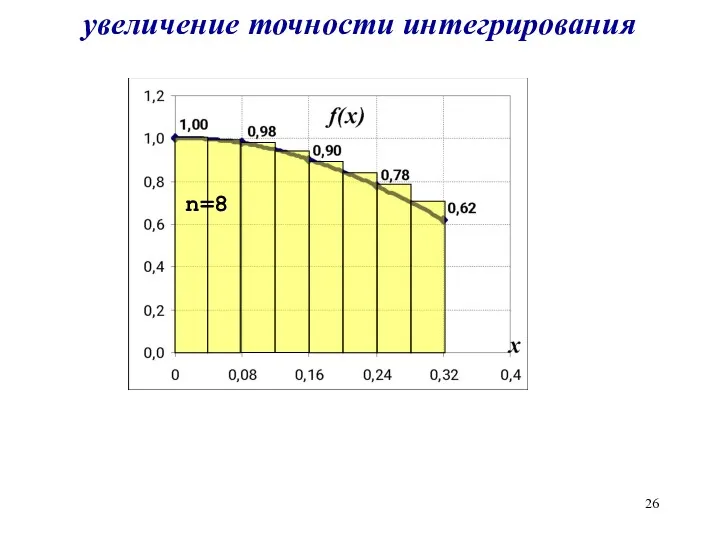
увеличение точности интегрирования
Слайд 27
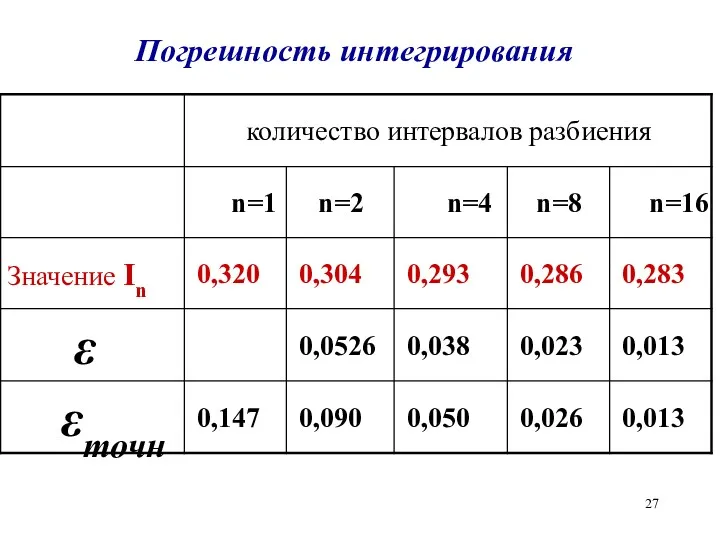
Погрешность интегрирования
Слайд 28
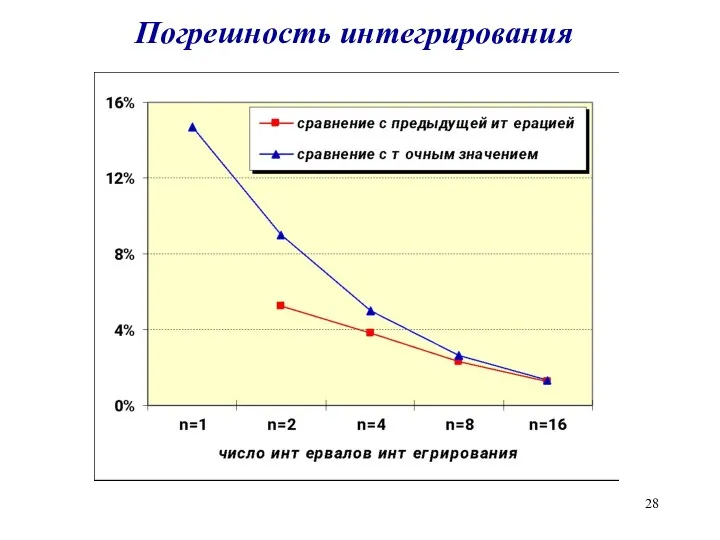
Погрешность интегрирования
Слайд 29

Символьное интегрирование в среде Matlab
syms x
f=sym(‘x/(4+x^2’)
s=int(f,x) – функция вычисляющая значение интеграла,
где
s – символьное значение интеграла
f –подынтегральная функция.
Слайд 30

Численное интегрирование в среде Matlab
a=0;
b=1;
s=int(‘x/(4+x^2’,a,b)
где
s – численное значение интеграла
a,
b – пределы интегрирования
Слайд 31

Численное интегрирование в среде Matlab
Метод трапеций:
s=trapz(x,y)
– функция вычисляющая значение интеграла
методом трапеций, где
s – численное значение интеграла
x – вектор значений аргумента
y – вектор значений подынтегральной функции.






























 Числовые промежутки
Числовые промежутки Возникновение жизни на Земле
Возникновение жизни на Земле Лев Николаевич Толстой (1828 – 1910)
Лев Николаевич Толстой (1828 – 1910) Конституція України - Основний закон держави
Конституція України - Основний закон держави Гидролиз солей
Гидролиз солей Основные средства предприятия
Основные средства предприятия презентация Герои Великой Отечественной войны А. Мнацаканов
презентация Герои Великой Отечественной войны А. Мнацаканов Мікропроцесорна техніка PSoC Creator 4.2 Designing with PSoC 3/5. (Лекція 5)
Мікропроцесорна техніка PSoC Creator 4.2 Designing with PSoC 3/5. (Лекція 5) Новогодняя открытка у году обезьяны
Новогодняя открытка у году обезьяны A little bit about Spimun
A little bit about Spimun Ценности западной культуры по мнению М. Вебера
Ценности западной культуры по мнению М. Вебера Поколения авиационных ГТД
Поколения авиационных ГТД Крыжацкая і татарская навала
Крыжацкая і татарская навала Презентация Проектная деятельность
Презентация Проектная деятельность О нашем классе.
О нашем классе. Царь колокол
Царь колокол Ты во мне поёшь, Азербайджан
Ты во мне поёшь, Азербайджан Печатающие устройства
Печатающие устройства Глагол can
Глагол can Пропорциональность отрезков хорд, касательных и секущих
Пропорциональность отрезков хорд, касательных и секущих Отчет о работе педагога группы № 4 за 2014-2015 учебный год
Отчет о работе педагога группы № 4 за 2014-2015 учебный год Электроснабжение ремонтно-механического цеха
Электроснабжение ремонтно-механического цеха Компьютерные игры в жанре экшен
Компьютерные игры в жанре экшен Дистрофии. Гипотрофия. Паратрофия. Гипостатура. Симптомы, диагностика, лечение, профилактика
Дистрофии. Гипотрофия. Паратрофия. Гипостатура. Симптомы, диагностика, лечение, профилактика Множества и операции над ними
Множества и операции над ними Система образования Германии
Система образования Германии Формула души. Обучающий курс
Формула души. Обучающий курс Интерактивная игра. Географическое лото. Африка.
Интерактивная игра. Географическое лото. Африка.