Содержание
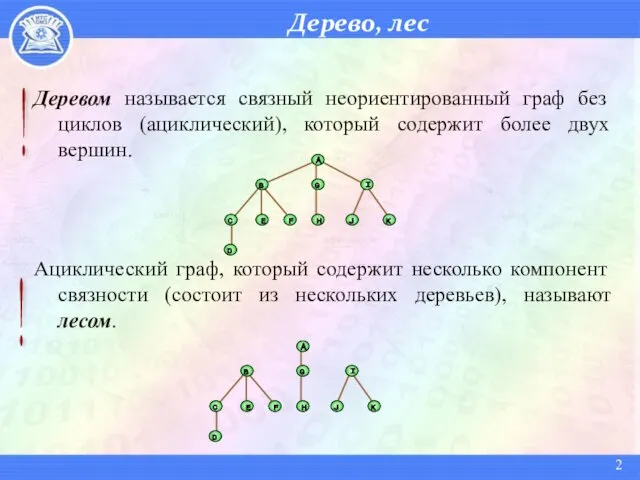
- 2. Дерево, лес Деревом называется связный неориентированный граф без циклов (ациклический), который содержит более двух вершин. Ациклический
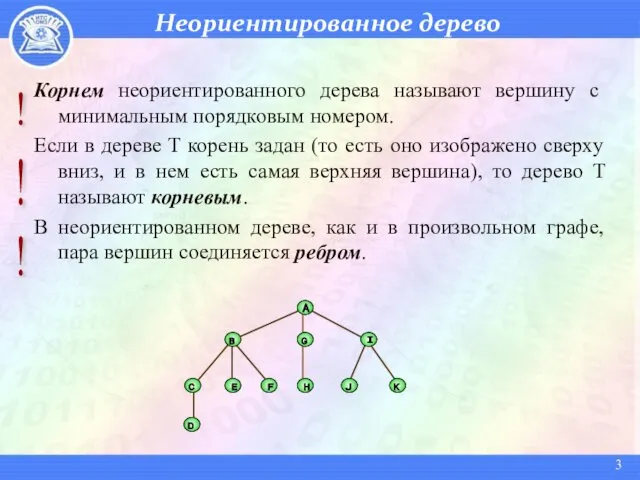
- 3. Неориентированное дерево B A G I C E F H J K D Корнем неориентированного дерева
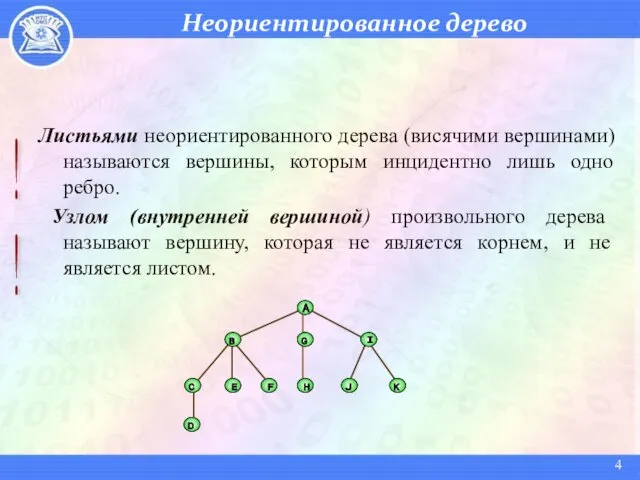
- 4. Неориентированное дерево B A G I C E F H J K D Листьями неориентированного дерева
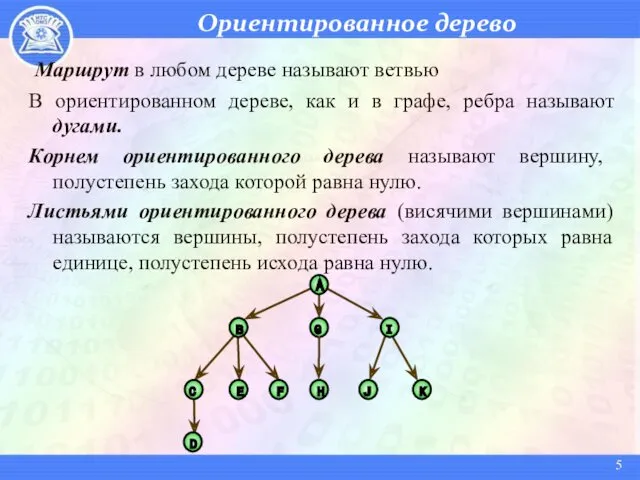
- 5. Ориентированное дерево Маршрут в любом дереве называют ветвью В ориентированном дереве, как и в графе, ребра
- 6. Свойства деревьев Для графа G(v,e) эквивалентны следующие утверждения: 1) G – дерево; 2) G – связный
- 7. Терминология, принятая в генеалогических деревьях При описании соотношений между узлами дерева используется терминология, принятая в генеалогических
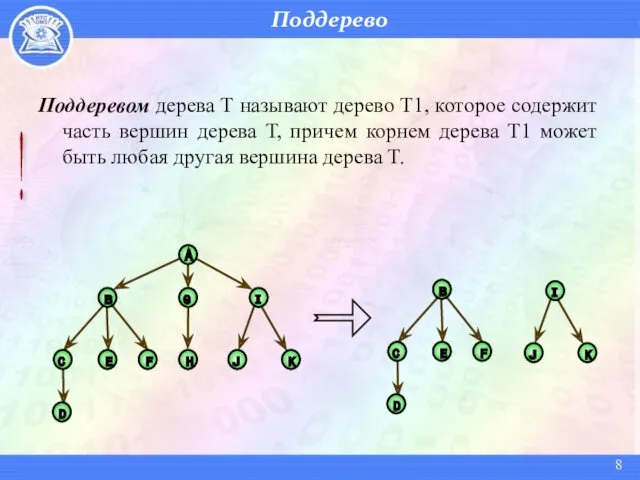
- 8. Поддерево Поддеревом дерева Т называют дерево Т1, которое содержит часть вершин дерева Т, причем корнем дерева
- 9. n-арное дерево Корневое дерево называется n-арным, если каждая внутренняя вершина имеет не более n детей. Порядком
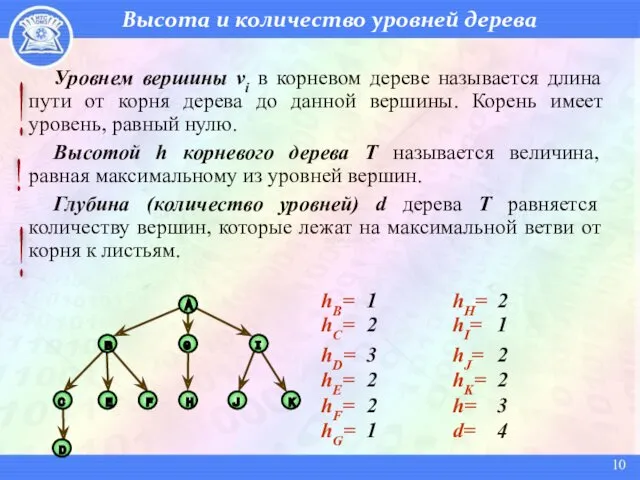
- 10. Высота и количество уровней дерева Уровнем вершины vi в корневом дереве называется длина пути от корня
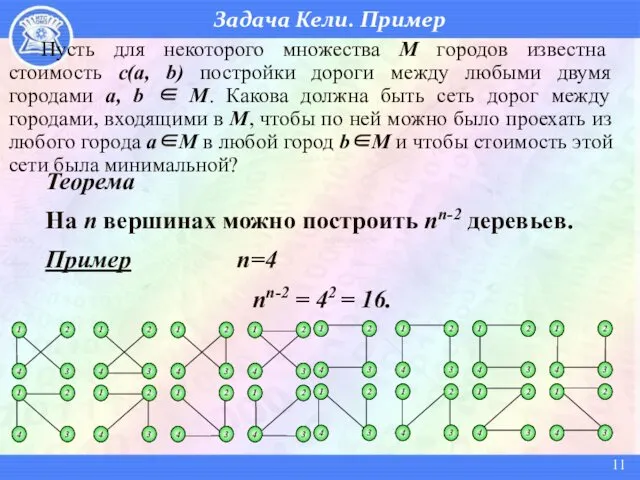
- 11. Задача Кели. Пример Пусть для некоторого множества М городов известна стоимость с(a, b) постройки дороги между
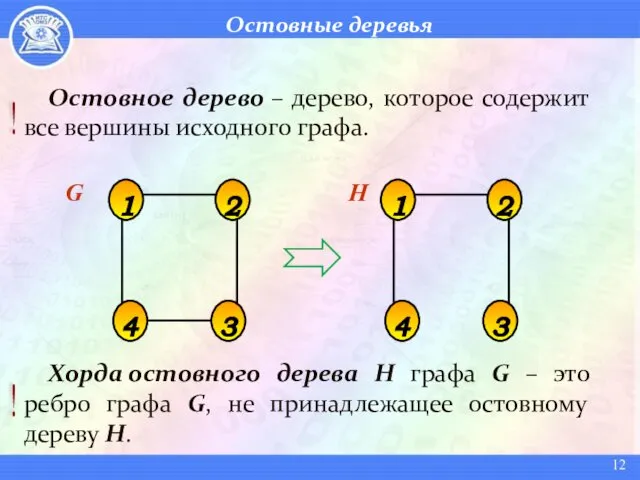
- 12. Остовные деревья Остовное дерево – дерево, которое содержит все вершины исходного графа. Хорда остовного дерева Н
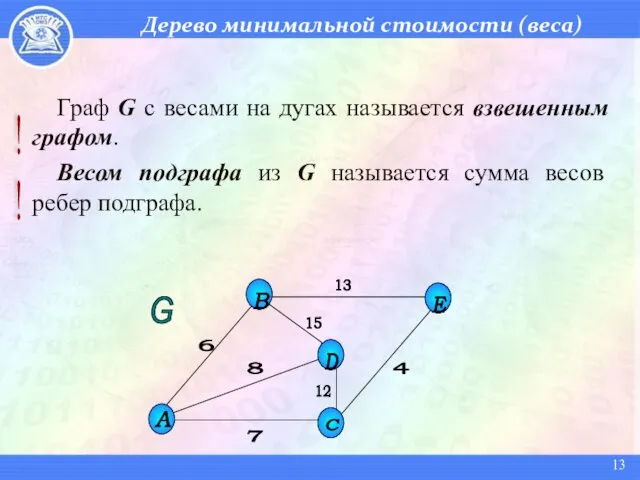
- 13. Дерево минимальной стоимости (веса) Граф G с весами на дугах называется взвешенным графом. Весом подграфа из
- 14. Алгоритм Борувки Упорядочиваем ребра в порядке возрастания их весов. Включаем в остовное дерево, ребра в порядке
- 15. Алгоритм Борувки. Пример Построить дерево минимальной стоимости для заданного графа G. С 7 А В D
- 16. Алгоритм кодирования деревьев 1) Вводится последовательность Np = (1, 2,..., р), где p – количество вершин
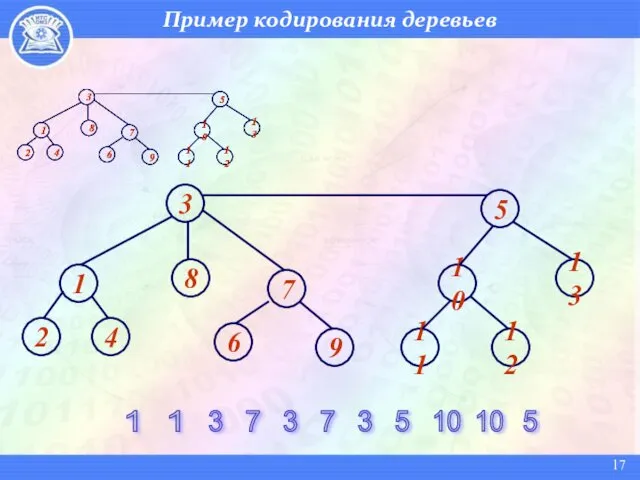
- 17. Пример кодирования деревьев 1 1 3 7 3 7 3 5 10 10 5 4 1
- 18. Алгоритм декодирования деревьев Находим общее количество вершин (количество вершин в коде дерева + 2); Находим висячие
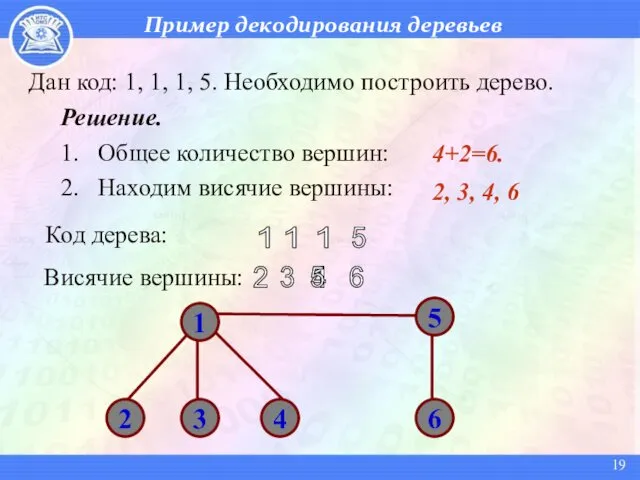
- 19. Пример декодирования деревьев Дан код: 1, 1, 1, 5. Необходимо построить дерево. Решение. 1. Общее количество
- 20. Бинарные деревья
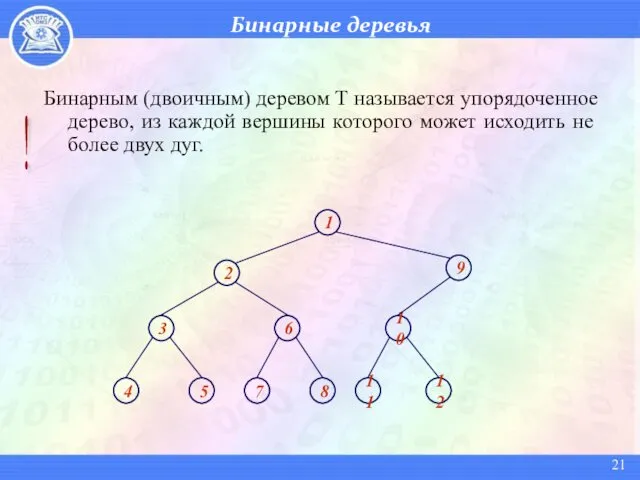
- 21. Бинарные деревья Бинарным (двоичным) деревом Т называется упорядоченное дерево, из каждой вершины которого может исходить не
- 22. Бинарные деревья Каждая вершина бинарного дерева может иметь либо двух сыновей – левого и правого, либо
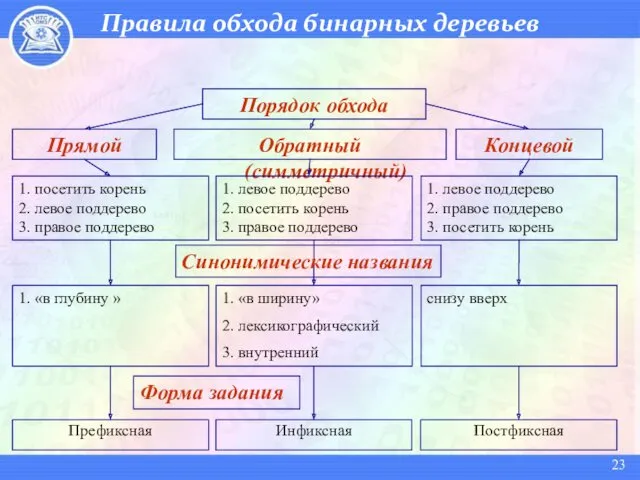
- 23. Правила обхода бинарных деревьев 1. «в глубину » 1. «в ширину» 2. лексикографический 3. внутренний снизу
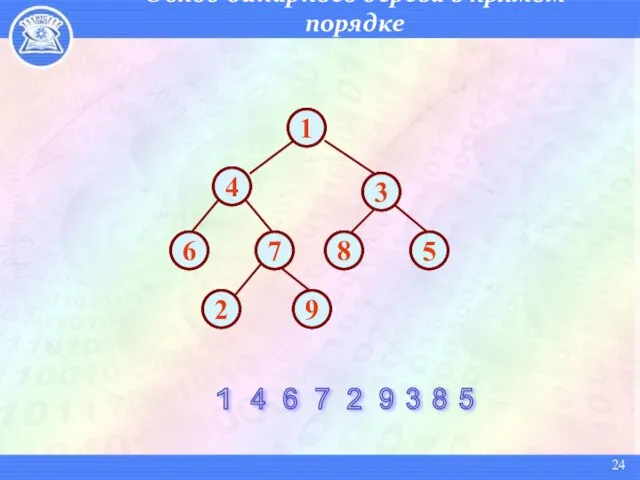
- 24. Обход бинарного дерева в прямом порядке 1 4 7 2 9 3 8 5 1 4
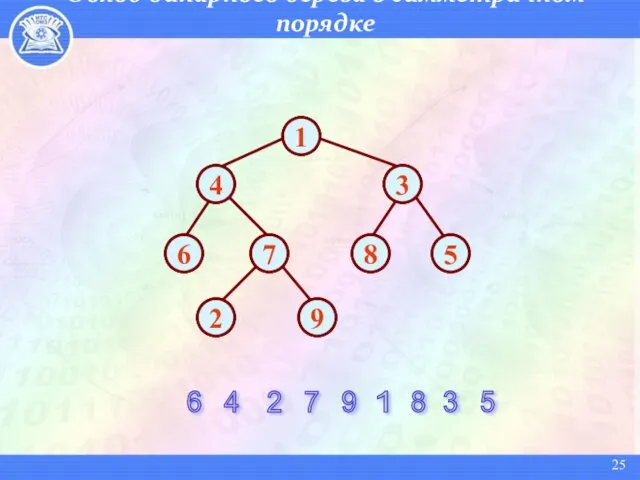
- 25. Обход бинарного дерева в симметричном порядке 6 4 2 7 9 1 8 3 5 6
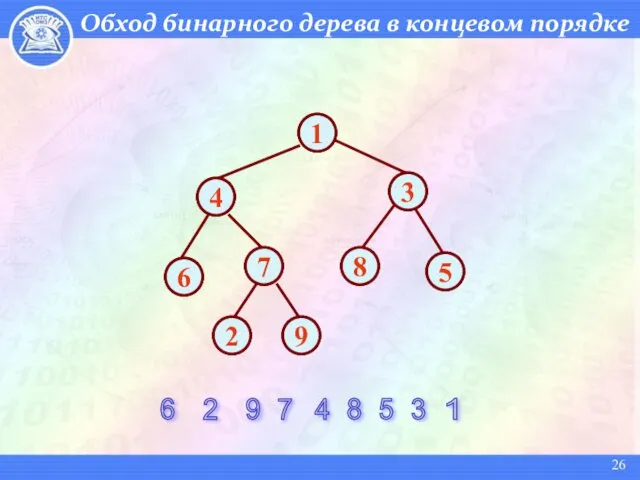
- 26. Обход бинарного дерева в концевом порядке 6 2 9 7 4 8 5 3 1 6
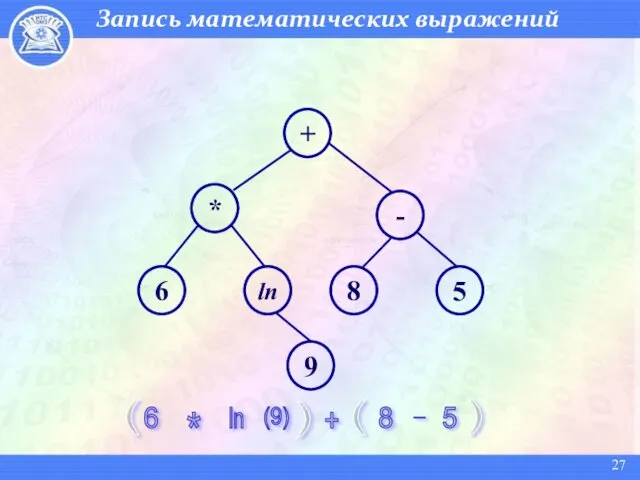
- 27. Запись математических выражений + * ln 9 - 8 5 6 6 * ln (9) +
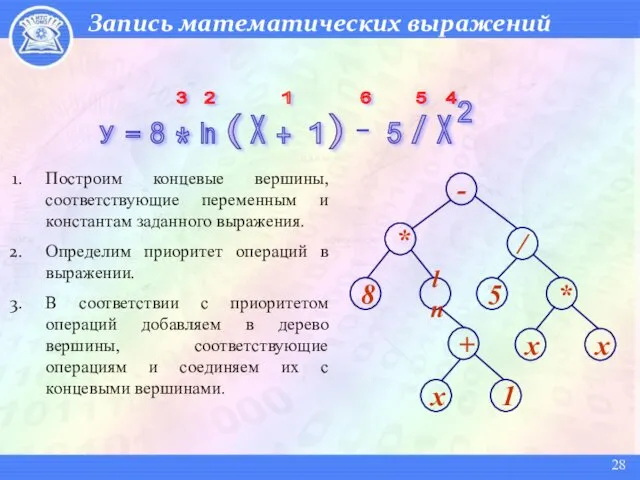
- 28. Запись математических выражений Х * ln + - 5 ) ( 1 8 / у =
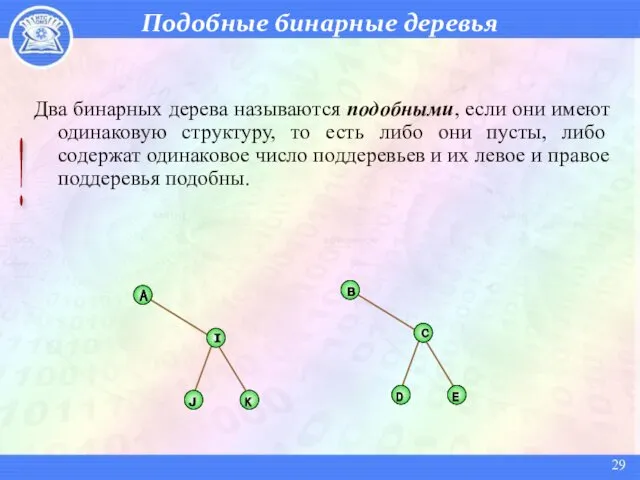
- 29. Подобные бинарные деревья Два бинарных дерева называются подобными, если они имеют одинаковую структуру, то есть либо
- 31. Скачать презентацию









 Выбор в условиях риска и неопределенности
Выбор в условиях риска и неопределенности Жевательная резинка - за и против
Жевательная резинка - за и против Праздник весны.
Праздник весны. Твердотельная электроника. Семинар №6
Твердотельная электроника. Семинар №6 Электризация тел. Два рода зарядов
Электризация тел. Два рода зарядов Времена глагола 2 класс
Времена глагола 2 класс Начало колониальных захватов и создания колониальных империй
Начало колониальных захватов и создания колониальных империй Топливно-энергетический комплекс Красноярского края
Топливно-энергетический комплекс Красноярского края Мікробіологія плодоовочевих товарів
Мікробіологія плодоовочевих товарів ЕГЭ по обществознанию. Работа с текстом на экзамене
ЕГЭ по обществознанию. Работа с текстом на экзамене Обобщающий урок по теме Глагол
Обобщающий урок по теме Глагол Особенности режимных моментов работы группы продленного дня для начальных классов
Особенности режимных моментов работы группы продленного дня для начальных классов Отто фон Бисмарк 1815-1898
Отто фон Бисмарк 1815-1898 Незулин. Показания, способ применения
Незулин. Показания, способ применения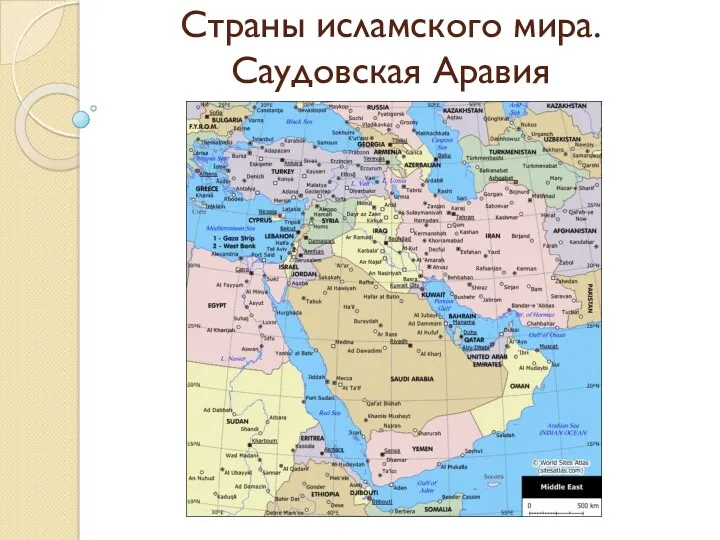 Страны исламского мира. Саудовская Аравия
Страны исламского мира. Саудовская Аравия 20230816_sera_himiya_9_klass
20230816_sera_himiya_9_klass Взаимодействие ДОУ и семьи
Взаимодействие ДОУ и семьи Формы взаимодействия психолога с коллективом
Формы взаимодействия психолога с коллективом Пожарная безопасность
Пожарная безопасность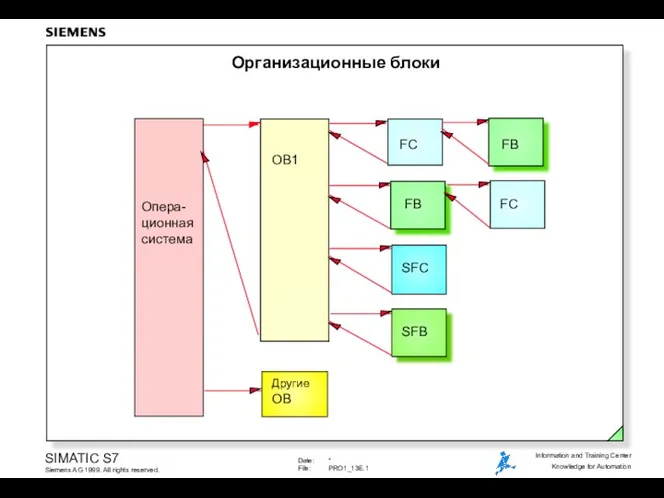 Организационные блоки
Организационные блоки Субъекты предпринимательского права. (Лекция 5)
Субъекты предпринимательского права. (Лекция 5) Игры Деда Буквоеда
Игры Деда Буквоеда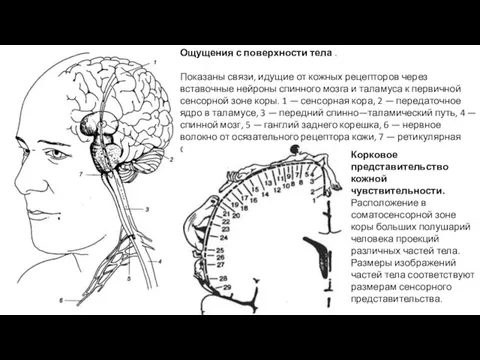 Ощущения с поверхности тела
Ощущения с поверхности тела Конституция России
Конституция России Неонталогия Наргиза
Неонталогия Наргиза Чай! Как он прекрасен! Вкусен! Крепок! Ароматен!
Чай! Как он прекрасен! Вкусен! Крепок! Ароматен! Төсләр 1нче сыйныфлар өчен татар теленнән презентация (рус төркеме)
Төсләр 1нче сыйныфлар өчен татар теленнән презентация (рус төркеме) Первые христиане и их учение
Первые христиане и их учение