Содержание
- 2. Outline Halo diagnostic: What is Halo? Halo Quantification Halo Measurements Some examples
- 3. What is Halo? “It is very difficult to give a simple definition of the “halo”. It
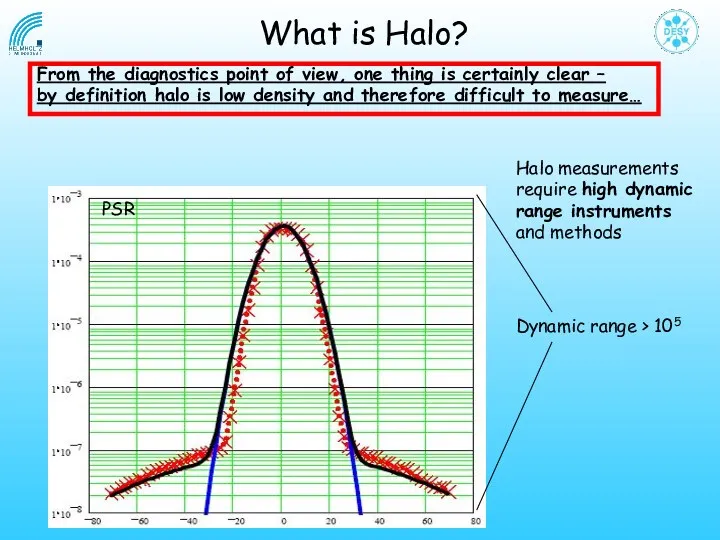
- 4. From the diagnostics point of view, one thing is certainly clear – by definition halo is
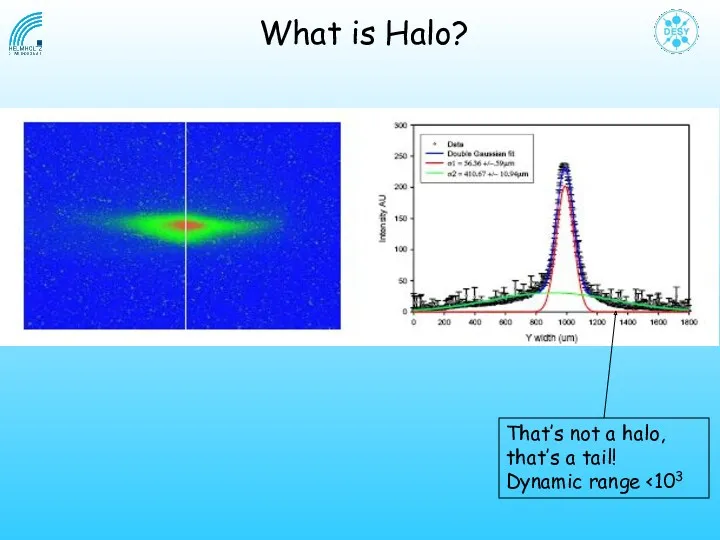
- 5. That’s not a halo, that’s a tail! Dynamic range What is Halo?
- 6. Sources of halo are: space charge forces of the beam Mismatch of beam with accel. optics
- 7. Outline Halo diagnostic: What is Halo? Halo Quantification Halo Measurements Some examples
- 8. It is important to have a definition of halo in 1D spatial projections for which experimental
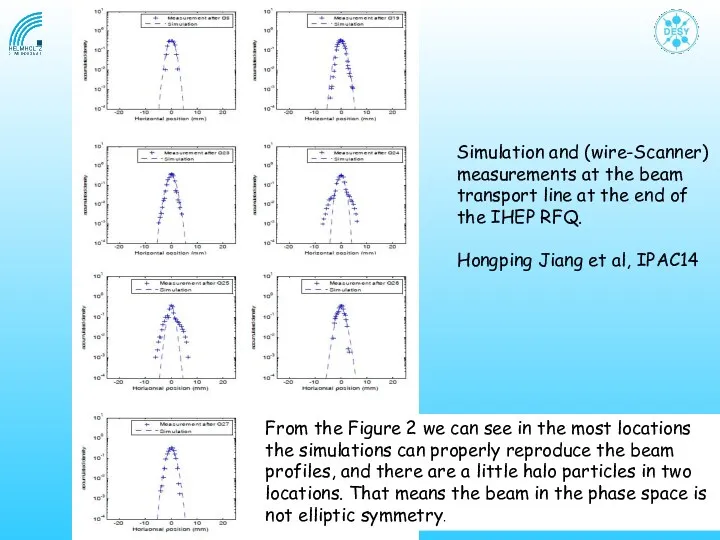
- 9. From the Figure 2 we can see in the most locations the simulations can properly reproduce
- 10. There is no clearly defined separation between the halo and the main core of the beam.
- 11. 1) Kurtosis This method is based on analyzing the fourth moment of the beam profile. The
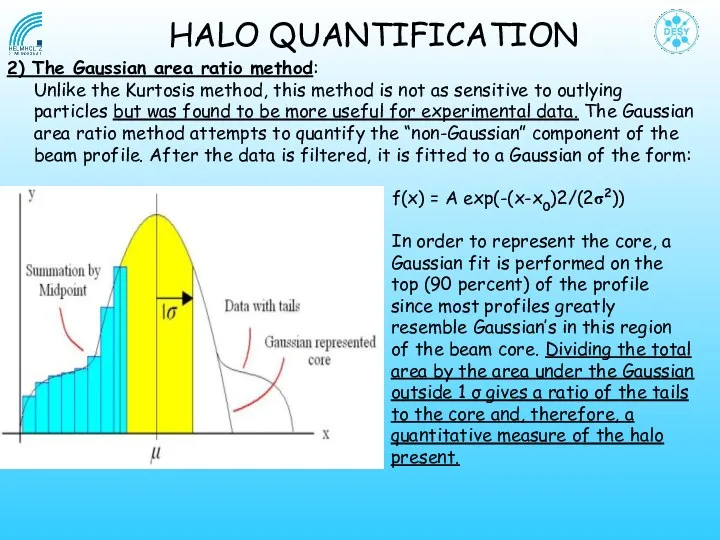
- 12. f(x) = A exp(-(x-x0)2/(2σ2)) In order to represent the core, a Gaussian fit is performed on
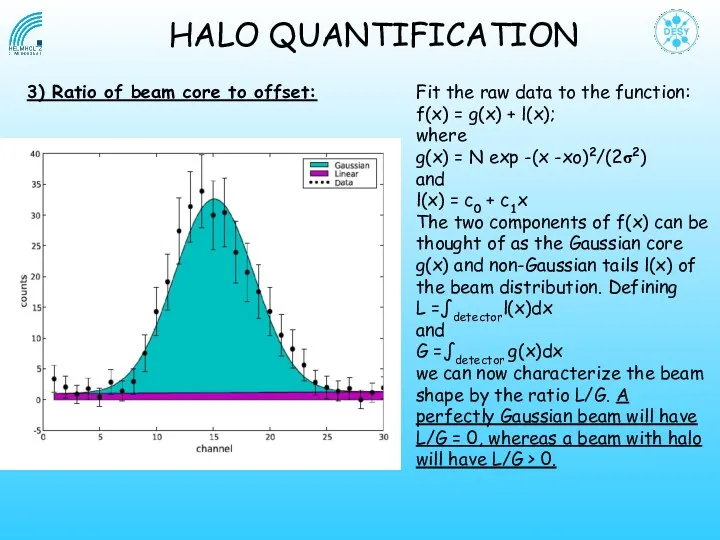
- 13. Fit the raw data to the function: f(x) = g(x) + l(x); where g(x) = N
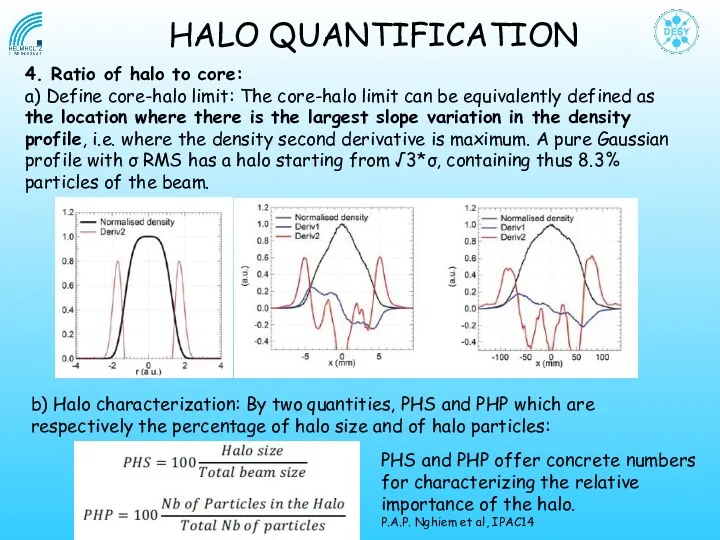
- 14. HALO QUANTIFICATION 4. Ratio of halo to core: a) Define core-halo limit: The core-halo limit can
- 15. Outline Halo diagnostic: What is Halo? Halo Quantification Halo Measurements Some examples
- 16. The focus of the accelerator physicists is on designing and operating their machines to minimize this
- 17. Profile monitors like Wire, IPM, LPM, Laser Wire, … are typically not designed for halo measurements.
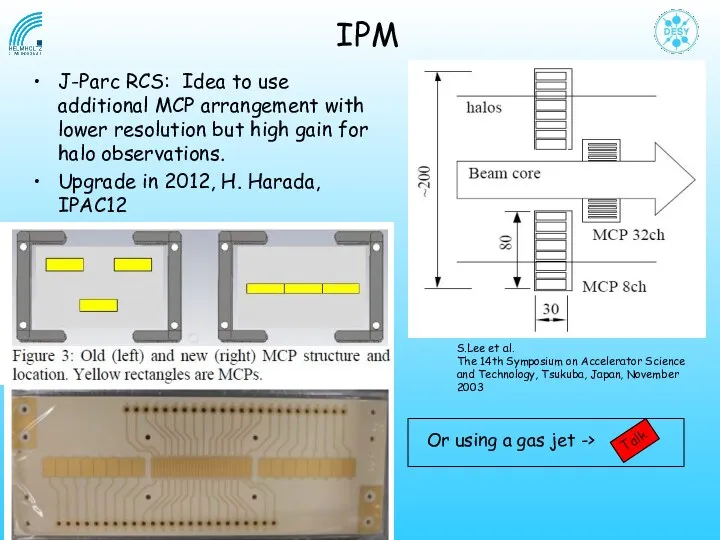
- 18. J-Parc RCS: Idea to use additional MCP arrangement with lower resolution but high gain for halo
- 19. Scraper data are spatially differentiated and averaged, Wire and scraper data are acquired with sufficient spatial
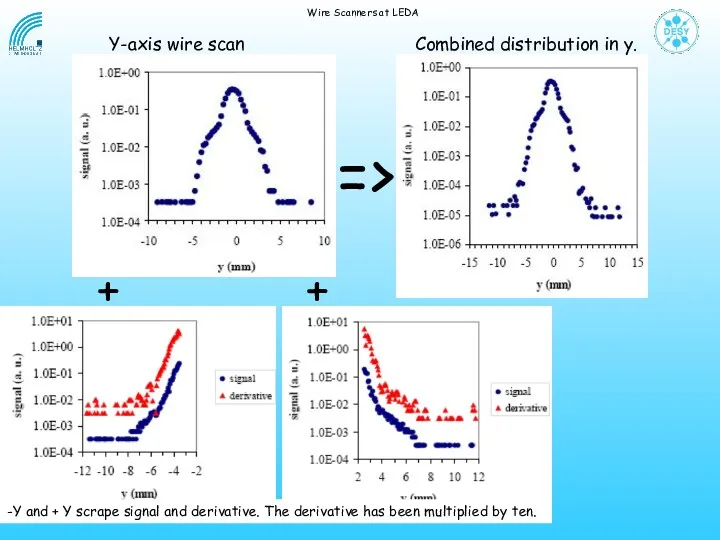
- 20. Wire Scanners at LEDA => + + -Y and + Y scrape signal and derivative. The
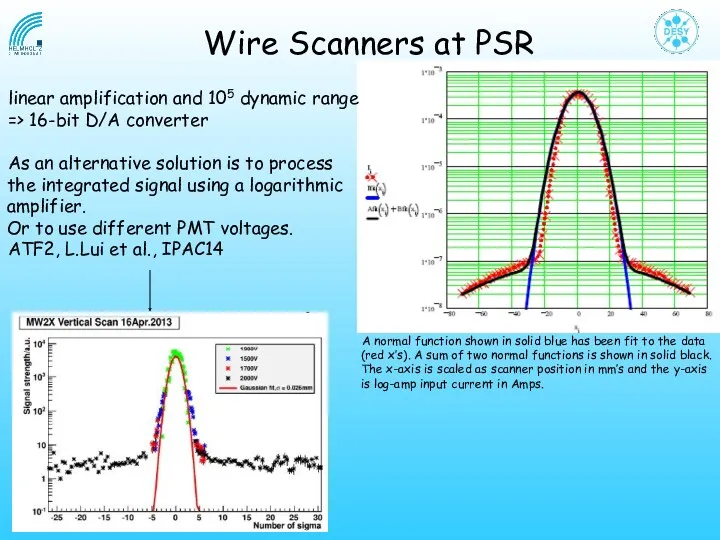
- 21. linear amplification and 105 dynamic range => 16-bit D/A converter As an alternative solution is to
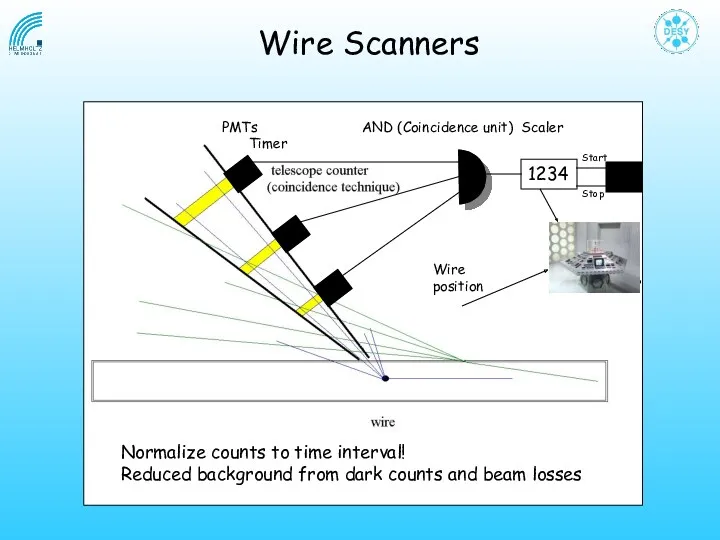
- 22. Wire Scanners PMTs AND (Coincidence unit) Scaler Timer 1234 Wire position Normalize counts to time interval!
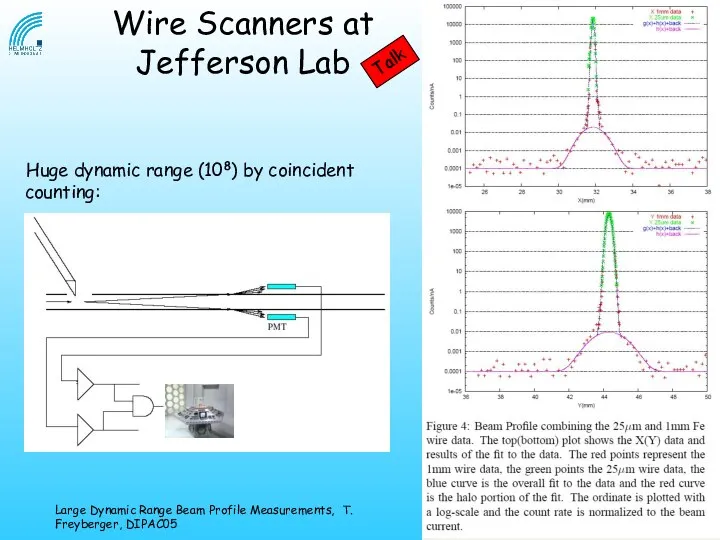
- 23. Huge dynamic range (108) by coincident counting: Wire Scanners at Jefferson Lab Talk Large Dynamic Range
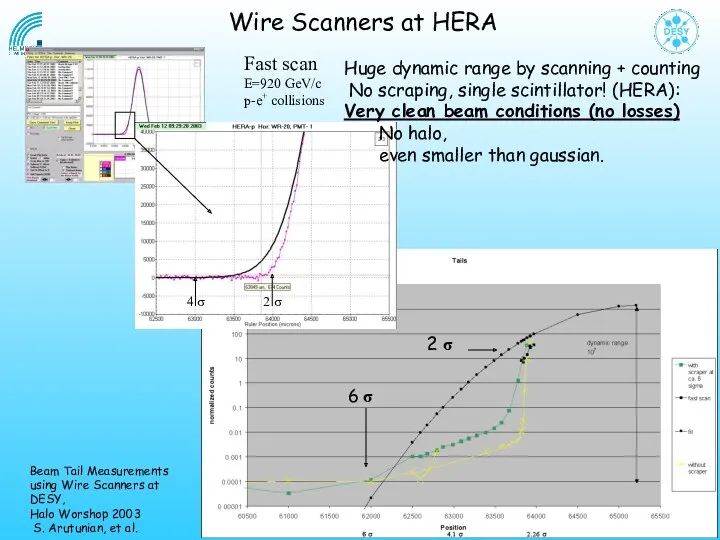
- 24. 4 σ 2 σ Fast scan E=920 GeV/c p-e+ collisions Huge dynamic range by scanning +
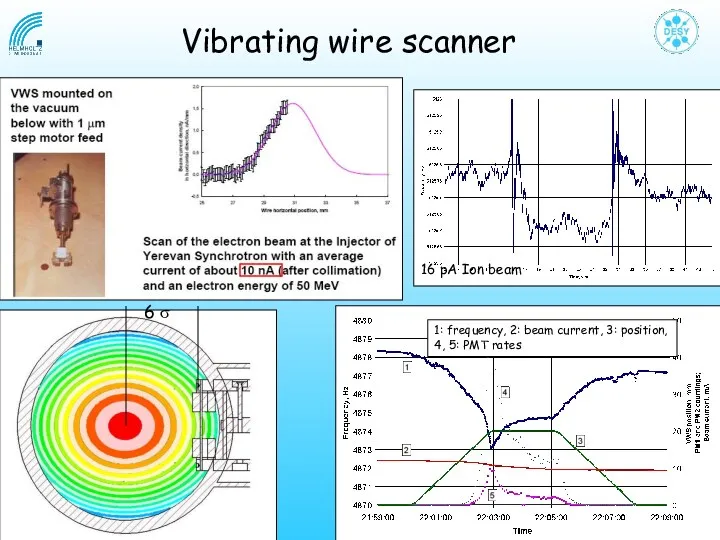
- 25. Vibrating wire scanner 6 σ
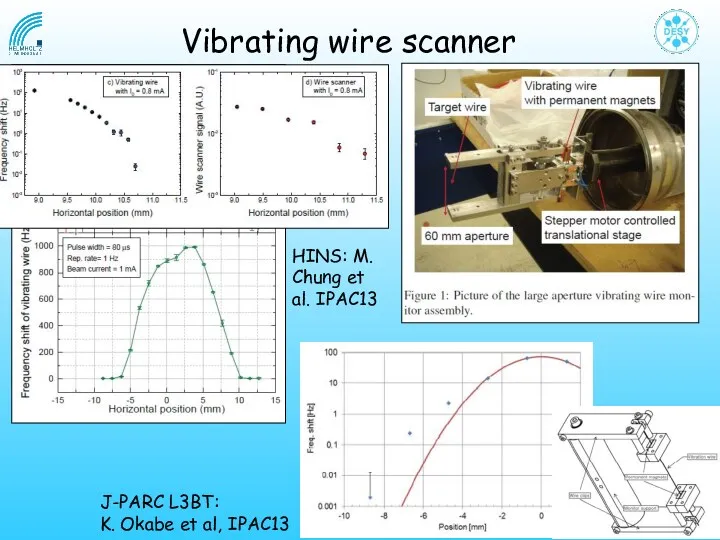
- 26. Vibrating wire scanner HINS: M. Chung et al. IPAC13 J-PARC L3BT: K. Okabe et al, IPAC13
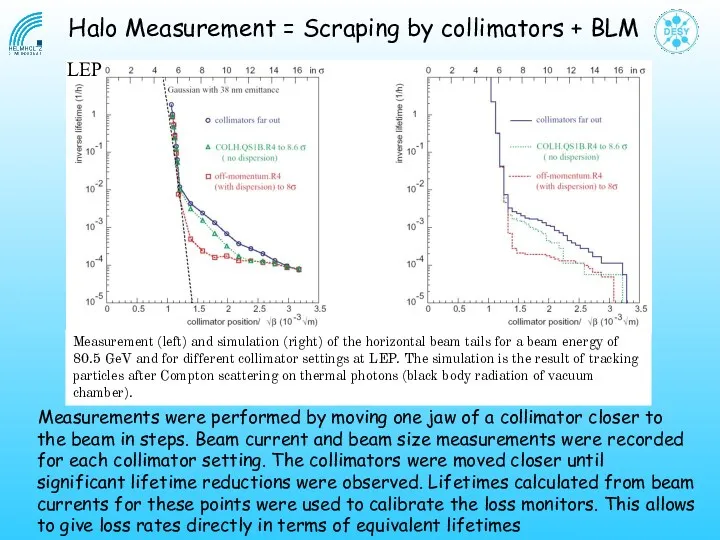
- 27. Halo scraping by collimators beam loss monitors x In a synchrotron one jaw will scrape both
- 28. Measurement (left) and simulation (right) of the horizontal beam tails for a beam energy of 80.5
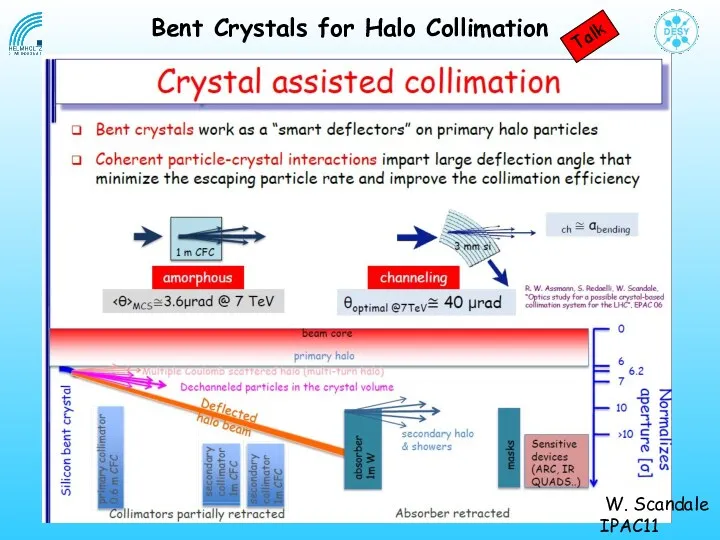
- 29. W. Scandale IPAC11 Bent Crystals for Halo Collimation Talk
- 30. Concept The hollow electron beam collimator is a cylindrical, hollow, magnetically confined, possibly pulsed electron beam
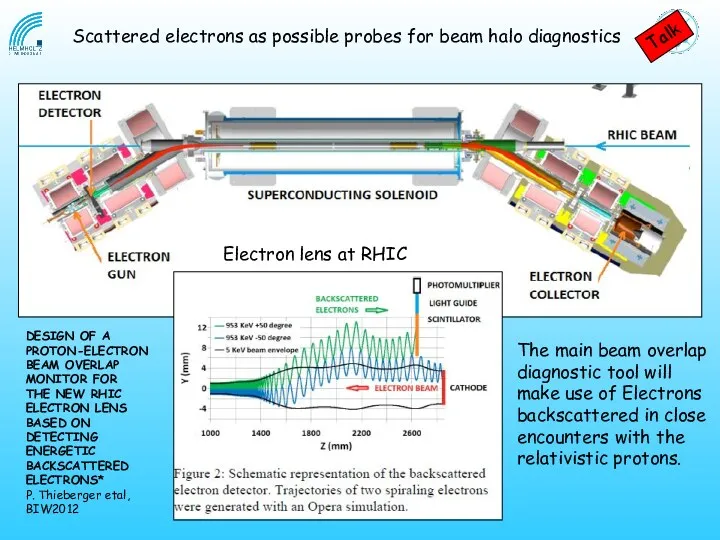
- 31. DESIGN OF A PROTON-ELECTRON BEAM OVERLAP MONITOR FOR THE NEW RHIC ELECTRON LENS BASED ON DETECTING
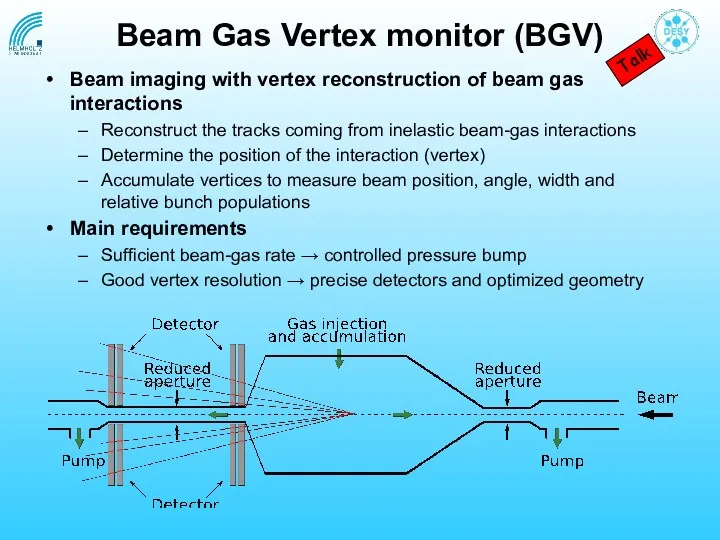
- 32. Beam Gas Vertex monitor (BGV) Beam imaging with vertex reconstruction of beam gas interactions Reconstruct the
- 33. Ion chamber, SEM PROSCAN Direct measurement by inserting monitor or by an intercepting monitor. No absolute
- 34. Optical Methods
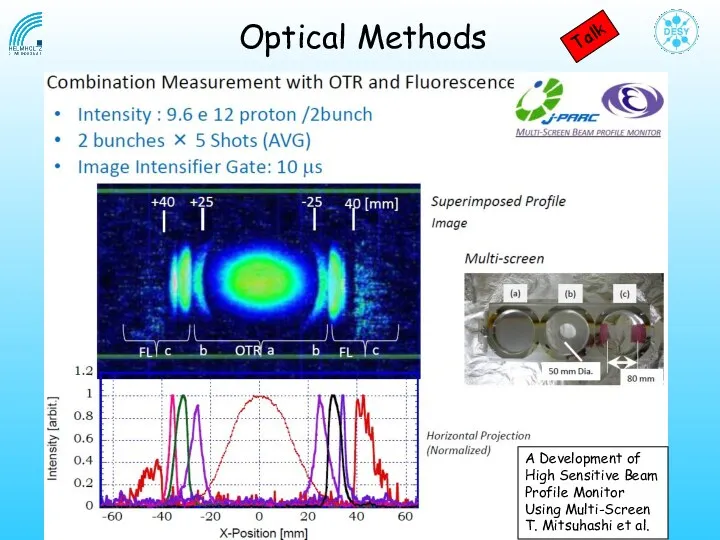
- 35. Optical Methods A Development of High Sensitive Beam Profile Monitor Using Multi-Screen T. Mitsuhashi et al.
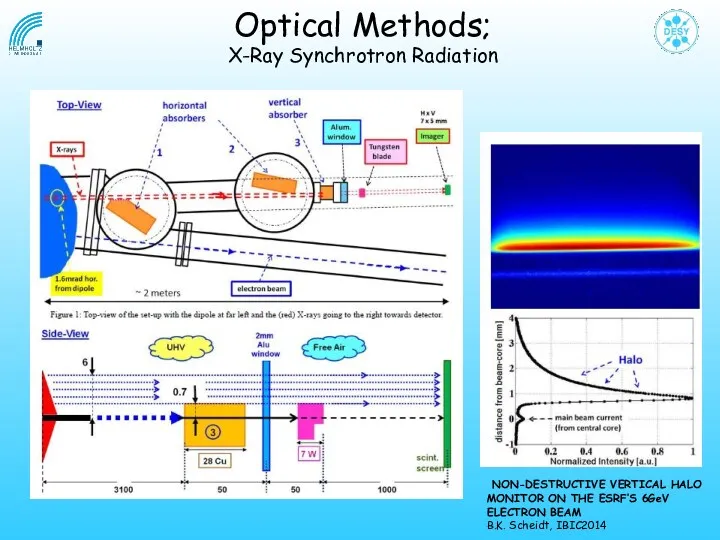
- 36. NON-DESTRUCTIVE VERTICAL HALO MONITOR ON THE ESRF’S 6GeV ELECTRON BEAM B.K. Scheidt, IBIC2014 Optical Methods; X-Ray
- 37. CID Camera Subarray Control RoI Each pixel on the CID array is individually addressable and allows
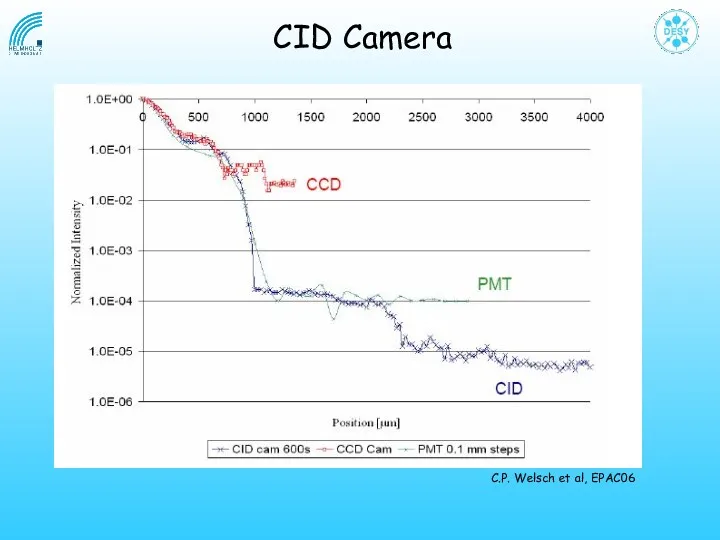
- 38. C.P. Welsch et al, EPAC06 CID Camera
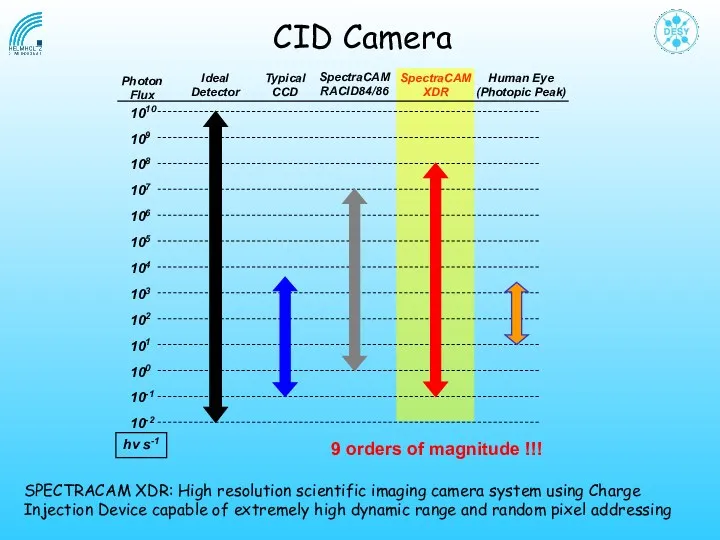
- 39. SPECTRACAM XDR: High resolution scientific imaging camera system using Charge Injection Device capable of extremely high
- 40. 1024 x 768 pixels (XGA) USB Interface high-speed port 64-bit @ 120 MHz for data transfer
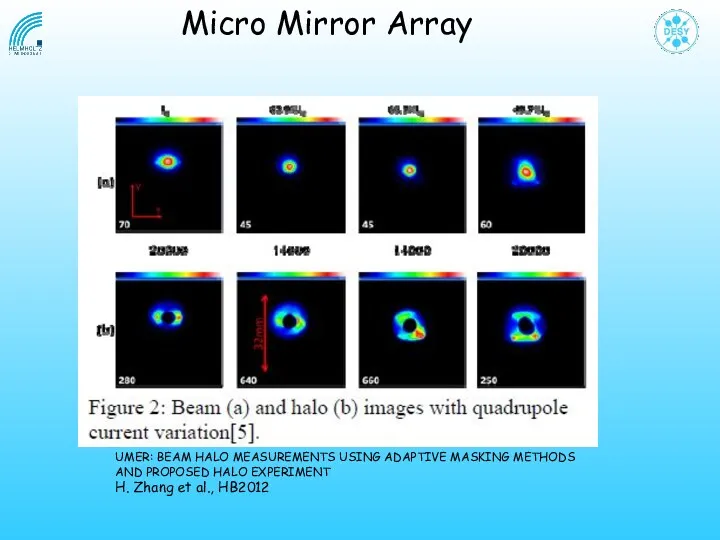
- 41. Micro Mirror Array UMER: BEAM HALO MEASUREMENTS USING ADAPTIVE MASKING METHODS AND PROPOSED HALO EXPERIMENT H.
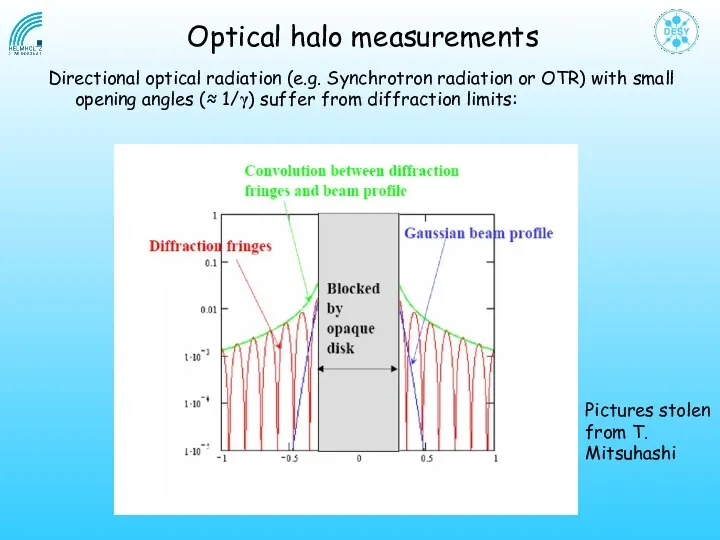
- 42. Directional optical radiation (e.g. Synchrotron radiation or OTR) with small opening angles (≈ 1/γ) suffer from
- 43. A coronagraph is a telescopic attachment designed specifically to block out the direct light from a
- 44. 9/19/2014 The End of the Introduction
- 46. Скачать презентацию



















 Нравственные диллемы начальной школы
Нравственные диллемы начальной школы Сосуды города
Сосуды города А.В.Суворов- гений военного искусства.
А.В.Суворов- гений военного искусства. Почему мы играем в ЛЕГО
Почему мы играем в ЛЕГО Полевые транзисторы
Полевые транзисторы ГБПОУ НАТК. Портфолио. Профессиональный модуль ПМ. 04
ГБПОУ НАТК. Портфолио. Профессиональный модуль ПМ. 04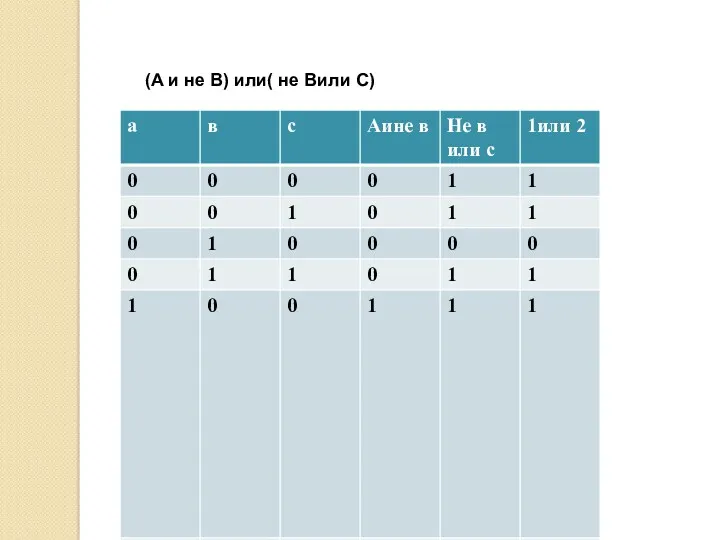 Триггеры, сумматоры
Триггеры, сумматоры Definitions of motivation
Definitions of motivation Коррекция фонематической дислексии
Коррекция фонематической дислексии Организация профориентационной работы: опыт, проблемы, перспективы
Организация профориентационной работы: опыт, проблемы, перспективы Тепломассообмен. Расчёт теплообменных аппаратов. (Лекция 14)
Тепломассообмен. Расчёт теплообменных аппаратов. (Лекция 14) Социальная сфера жизни общества
Социальная сфера жизни общества Познавательное мероприятие для младших школьников Жизнь без опасности
Познавательное мероприятие для младших школьников Жизнь без опасности Материалы по внесению изменений в ПЗЗ в части технико-экономических показателей и ВРИ по объекту
Материалы по внесению изменений в ПЗЗ в части технико-экономических показателей и ВРИ по объекту Оказание первой доврачебной помощи
Оказание первой доврачебной помощи Подключение к Tele2. Тарифы и услуги
Подключение к Tele2. Тарифы и услуги Пародонтологиядағы иммунотерапия
Пародонтологиядағы иммунотерапия Тромбоцитопеническая пурпура (ТПП)
Тромбоцитопеническая пурпура (ТПП) Padezhi_imen_suschestvitelnykh
Padezhi_imen_suschestvitelnykh Методические разработки уроков, полевых практик и лабораторных работ. 8класс
Методические разработки уроков, полевых практик и лабораторных работ. 8класс Психология рекламы
Психология рекламы Capitolul III. Logistica în amonte
Capitolul III. Logistica în amonte Мониторинг уровня сформированности у детей коммуникативных умений
Мониторинг уровня сформированности у детей коммуникативных умений Ноотропы
Ноотропы Учебный тренажёр и проверочный тест по теме: Члены предложения
Учебный тренажёр и проверочный тест по теме: Члены предложения Презентация Детям о дне Победы
Презентация Детям о дне Победы Бурибаевская солнечная электростанция
Бурибаевская солнечная электростанция Структура образовательной деятельности (занятий) в соответствий с ФГОС в ДО
Структура образовательной деятельности (занятий) в соответствий с ФГОС в ДО