Содержание
- 2. Парная линейная регрессия Основная цель – построить уравнение (модель) вида: описывающее зависимость между зависимой переменной (результатом
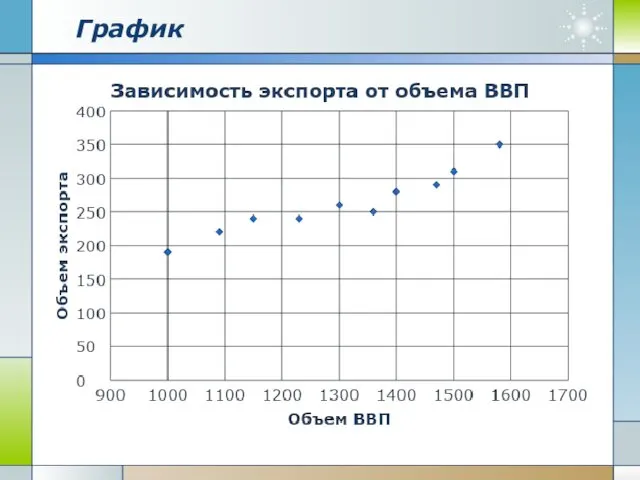
- 3. Изучается влияние объема ВВП на объем экспорта в стране. Для корреляционно-регрессионного анализа использована выборка за 10
- 4. График
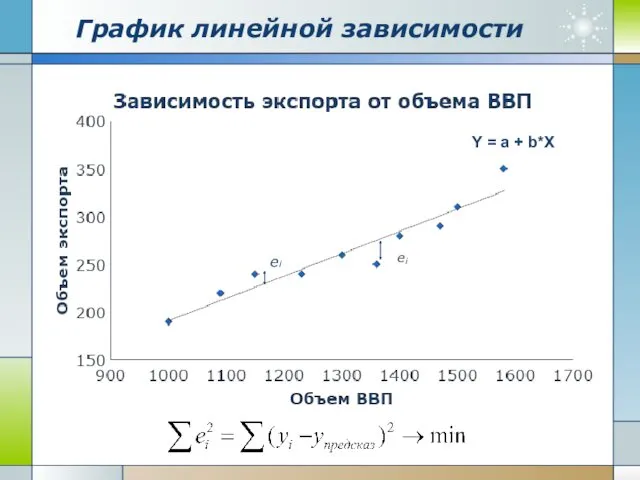
- 5. График линейной зависимости Y = a + b*X ei
- 6. Формулы для нахождения параметров При помощи метода наименьших квадратов (МНК) выведены формулы для нахождения параметров уравнения
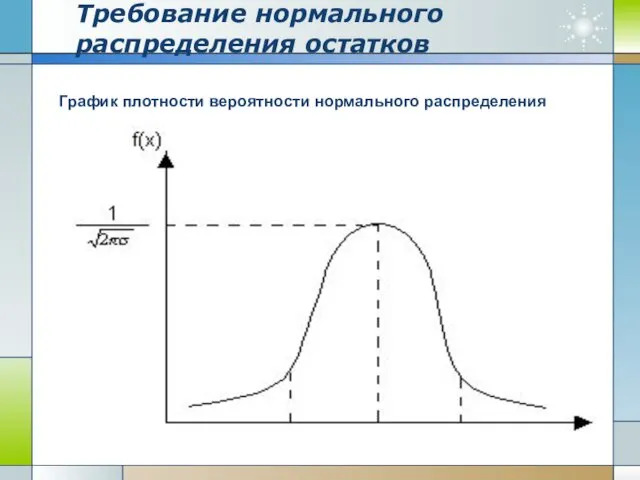
- 7. Требование нормального распределения остатков График плотности вероятности нормального распределения
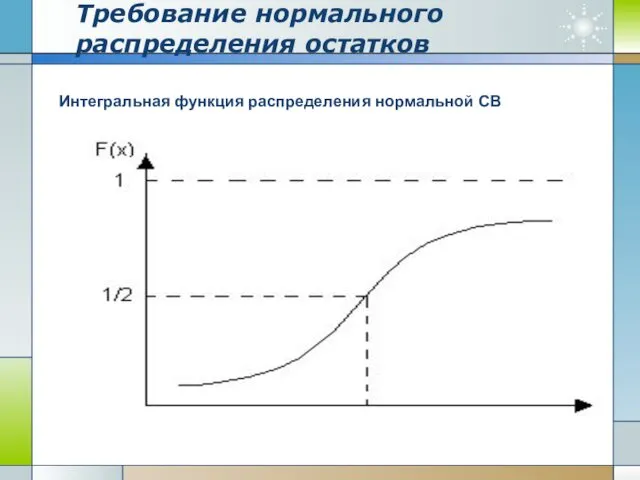
- 8. Требование нормального распределения остатков Интегральная функция распределения нормальной СВ
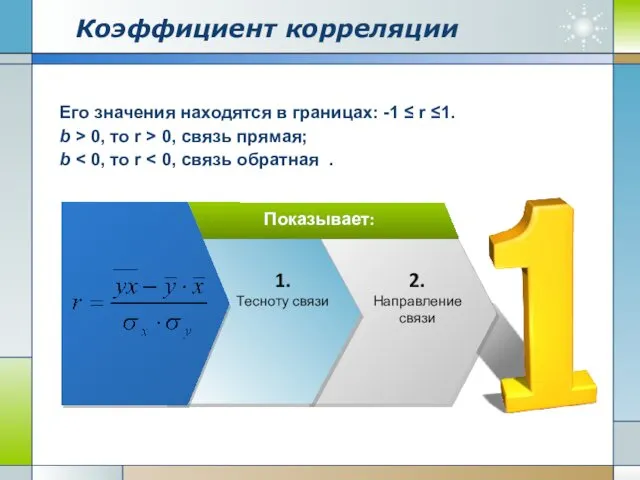
- 9. Коэффициент корреляции Показывает: 2. Направление связи Его значения находятся в границах: -1 ≤ r ≤1. b
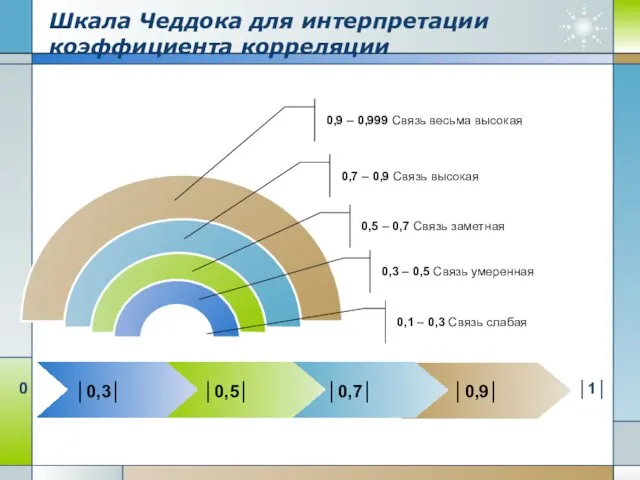
- 10. Шкала Чеддока для интерпретации коэффициента корреляции 0,1 – 0,3 Связь слабая 0,3 – 0,5 Связь умеренная
- 11. Проверка качества подбора модели (вида уравнения) Коэффициент детерминации R2- характеризует долю объясненной регрессией вариации y, в
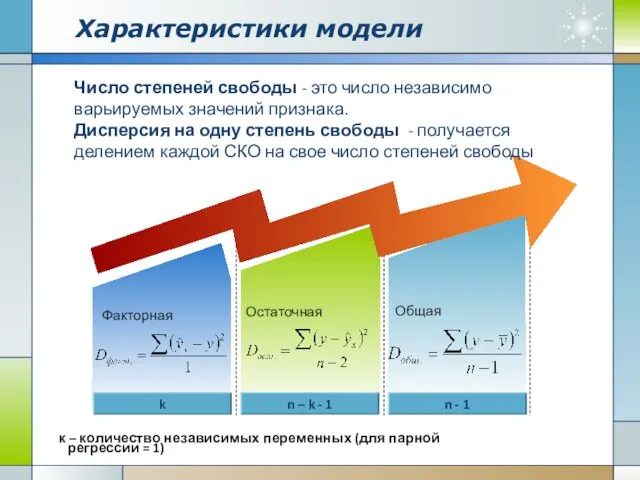
- 12. Характеристики модели n - 1 Факторная n – k - 1 k Остаточная Общая Число степеней
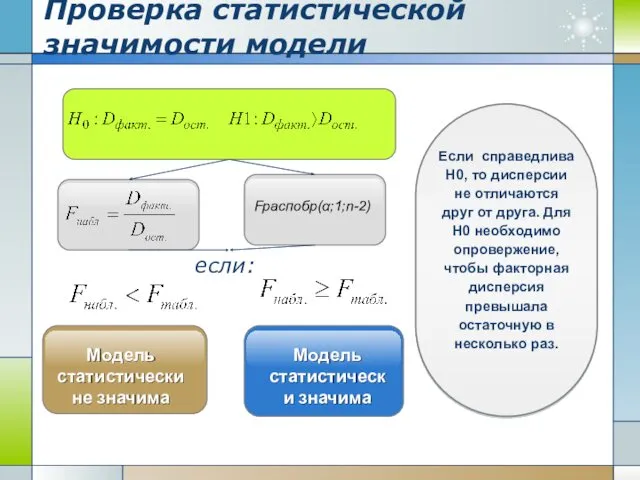
- 13. Проверка статистической значимости модели Fраспобр(α;1;n-2) Модель статистически не значима Модель статистически значима если: Если справедлива Н0,
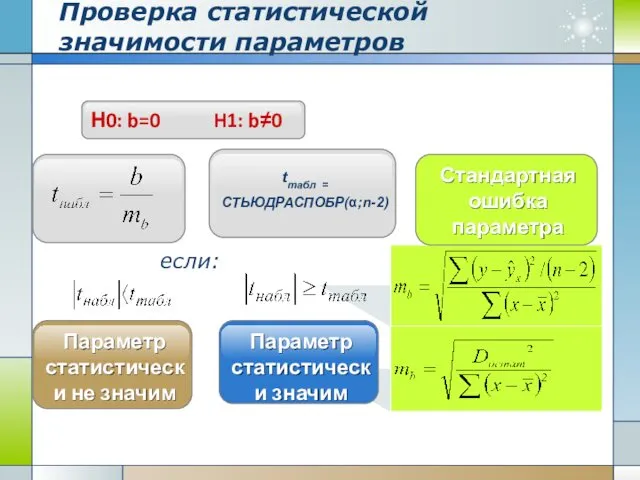
- 14. Проверка статистической значимости параметров Н0: b=0 H1: b≠0 tтабл = СТЬЮДРАСПОБР(α;n-2) Стандартная ошибка параметра Параметр статистически
- 15. Доверительный интервал для параметра параметр b с надежностью α лежит в интервале: значимость (α) = 1
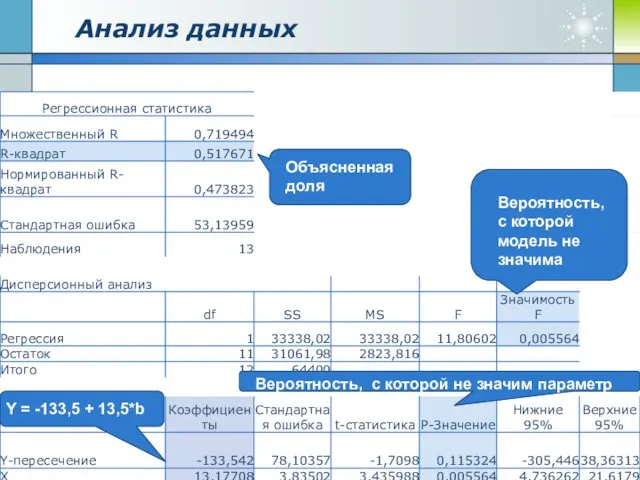
- 16. Анализ данных Y = -133,5 + 13,5*b Вероятность, с которой модель не значима Вероятность, с которой
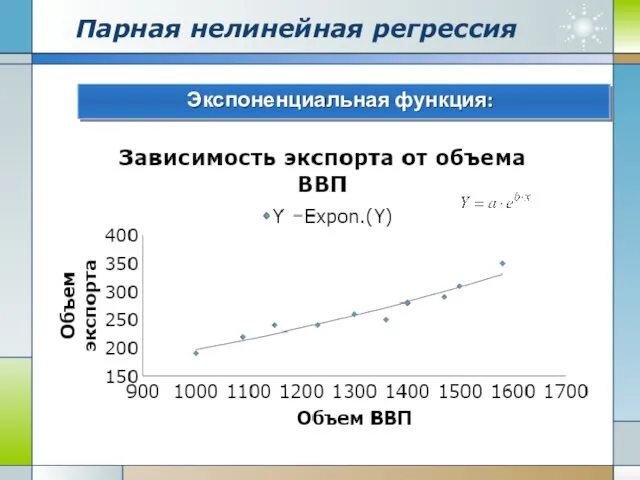
- 17. Парная нелинейная регрессия Экспоненциальная функция:
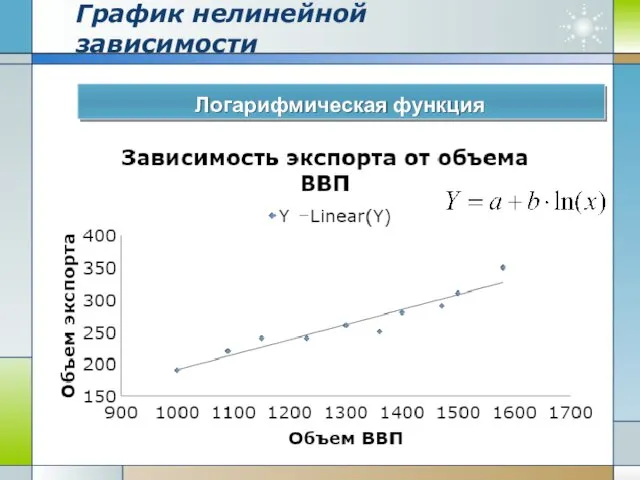
- 18. График нелинейной зависимости Логарифмическая функция
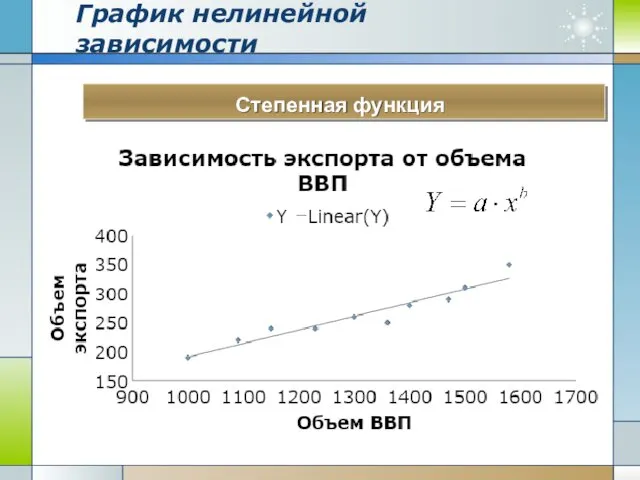
- 19. График нелинейной зависимости Describe a vision of company or strategic contents. Степенная функция
- 20. Эластичность Эластичность определяется по формуле: Для парной регрессии: Для степенной:
- 21. Уравнение множественной регрессии Линейная модель: На любой экономический показатель чаще всего оказывает влияние не один, а
- 22. Уравнение множественной регрессии в стандартизированном масштабе Уравнение регрессии в стандартизованном масштабе имеет вид: стандартизированные параметры: Система
- 23. Проверка качества уравнения множественной регрессии Коэффициент детерминации: Скорректированный к-т детерминации:
- 25. Скачать презентацию









 Вакцинація. Найпоширеніші міфи
Вакцинація. Найпоширеніші міфи Космическое путешествие
Космическое путешествие Роль домашнего задания в самообразовании школьника
Роль домашнего задания в самообразовании школьника e0f2d-a27ace3f
e0f2d-a27ace3f Disneyland is a dream of each child! Welcome to disneyland!!!
Disneyland is a dream of each child! Welcome to disneyland!!! Функции управления
Функции управления Конфликт воспитатель-родитель. Причины возникновения и пути решения
Конфликт воспитатель-родитель. Причины возникновения и пути решения Достоинства и недостатки ГЭС
Достоинства и недостатки ГЭС Inventions that shook the world
Inventions that shook the world Духовная сфера общества. Подготовка к ЕГЭ
Духовная сфера общества. Подготовка к ЕГЭ Социальная структура общества. Социология
Социальная структура общества. Социология Масленица
Масленица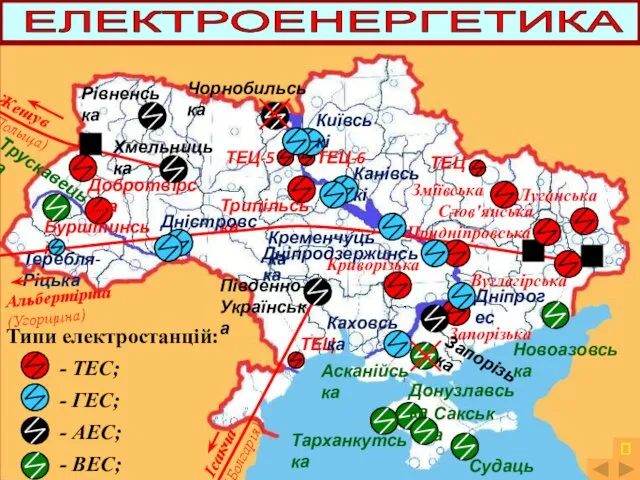 Карта електроенергетика
Карта електроенергетика DVB-T2. Стандарт наземного цифрового телевизионного вещания второго поколения
DVB-T2. Стандарт наземного цифрового телевизионного вещания второго поколения Основные аспекты иммунопрофилактики инфекционных заболеваний
Основные аспекты иммунопрофилактики инфекционных заболеваний Жыпылықтаушы аритмиясы бар науқастардың өмір сүру сапасы
Жыпылықтаушы аритмиясы бар науқастардың өмір сүру сапасы Правила заполнения корректирующих форм cведений (раздел 6 расчета РСВ-1)
Правила заполнения корректирующих форм cведений (раздел 6 расчета РСВ-1) Презентация к уроку по теме: Дикие и домашние животные
Презентация к уроку по теме: Дикие и домашние животные Варианты системы обнаружения утечек межпромыслового нефтепровода УПСВ Северный Савинобор
Варианты системы обнаружения утечек межпромыслового нефтепровода УПСВ Северный Савинобор Награды Великой Отечественной войны
Награды Великой Отечественной войны Публицистический стиль речи
Публицистический стиль речи презентация на тему: Современный урок в свете внедрения ФГОС второго поколения
презентация на тему: Современный урок в свете внедрения ФГОС второго поколения Аффект. Виды аффектов
Аффект. Виды аффектов Описание и преобразование управляющих процессов. Сети Петри и их модификация
Описание и преобразование управляющих процессов. Сети Петри и их модификация Социально-экономические проблемы региона. Химическая и нефтехимическая промышленность Республики Татарстан
Социально-экономические проблемы региона. Химическая и нефтехимическая промышленность Республики Татарстан Возможность жизни на других планетах
Возможность жизни на других планетах Етика і деонтологія в професійній діяльності лікаря
Етика і деонтологія в професійній діяльності лікаря Эрнест Хемингуэй
Эрнест Хемингуэй