Интеграл от функции комплексного переменного; теорема Коши для составного контура, интегральная теорема Коши. Лекция 33 презентация
Содержание
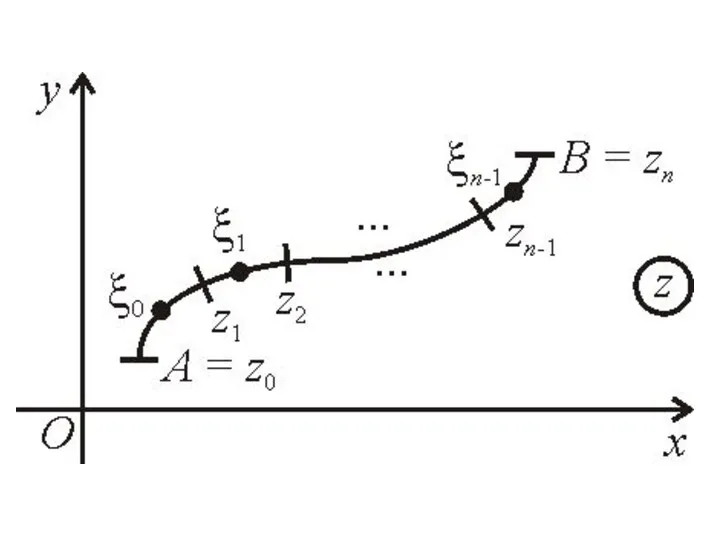
- 2. § 1. Интегрирование функции комплексного переменного. Пусть на комплексной плоскости задана кривая AB – ориентированная, незамкнутая,
- 4. α и β – действительные числа. x(t), y(t) – действительные числа. Разобьем AB произвольным образом: Найдем
- 5. Они отвечает соответствующим комплексным числам. Пусть на комплексной плоскости, в том числе и на дуге AB
- 6. Определение. (интеграла) Если существует предел интегральной суммы не зависящий от способа разбиения дуги AB и выбора
- 7. Теорема. (о существовании интеграла от функции комплексного переменного) Пусть функция f(x) непрерывна на некоторой кривой L,
- 8. Так как любую функцию комплексного переменного можно представить в виде: Комплексное число можно представить в виде
- 9. Значит в использованном выражении (1), интегральная сумма может быть записана в виде: (2) Перейдем к пределу
- 10. Так как f(z) непрерывна на L, то непрерывны в любой точке u и v (т.к задание
- 11. Так как каждый из пределов входящий, входящий в правую часть (3) существует и равен соответствующему криволинейному
- 12. Свойства интегралов от ФКП. Если L+ и L- две дуги, различающиеся только ориентацией, то: 2) 3)
- 13. § 2. Понятие первообразной. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной. Пусть функция f(z) задана
- 14. Теорема. (о первообразной) Если функция f(z) дифференцируема в замкнутой, односвязной области D, то для нее существует
- 15. Замечание 2: Если f(z) непрерывна в односвязной области D, и интеграл по любому замкнутому контуру, лежащему
- 16. Теорема. (Ньютона- Лейбница) Если f(z) дифференцируема в односвязной области D и z1, z0 произвольные точки D,
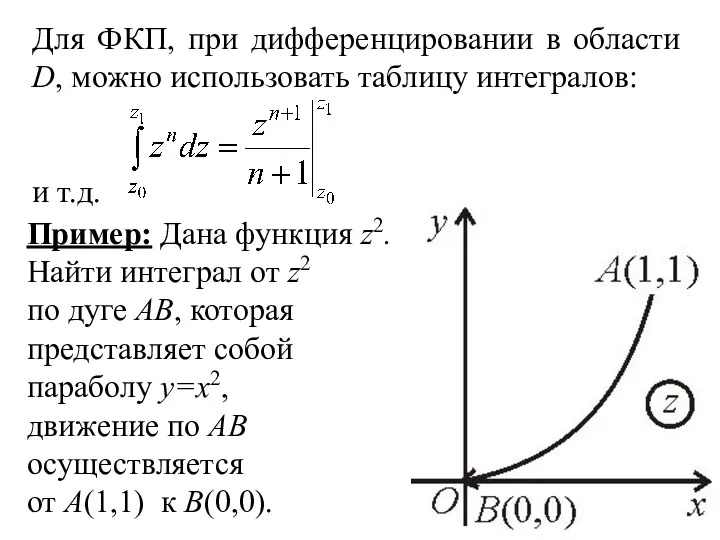
- 17. Пример: Дана функция z2. Найти интеграл от z2 по дуге AB, которая представляет собой параболу y=x2,
- 18. z2 = (x + iy)2 = x2 – y2 + i2xy u v тогда:
- 19. 2-й способ решения с помощью формулы Ньютона-Лейбница:
- 20. § 3. Интегральная теорема Коши. Если функция f(z) аналитична в односвязной замкнутой области D, то интеграл
- 21. Из аналитичности следует выполнение условий Коши-Римана Пусть L - произвольный, ориентированный замкнутый контур, в области D,
- 22. 0 0 D* - область, лежащая внутри L Из условий Коши-Римана имеем, что подынтегральное выражение =
- 23. Теорема. Если функция f (z) аналитична в неодносвязанной замкнутой области D с конечным числом вырезов, то
- 24. Li – граница вырезов, обход которой производится в том же направлении, что и обход границы L.
- 25. Примечание. Значения функции в области определяются своими значениями на границе. Без доказательства. Интеграл Коши Пусть функция
- 26. Свойства интеграла Коши Если z лежит вне контура L, z ∈ D, то для ∀ z
- 27. Если кривая L незамкнута, то говорят об интеграле типа Коши где Λ - незамкнутая ориентируемая кривая,
- 28. Замечание. Если функция f (z) дифференцируема в области D, кривая L замкнутая граница области D, то
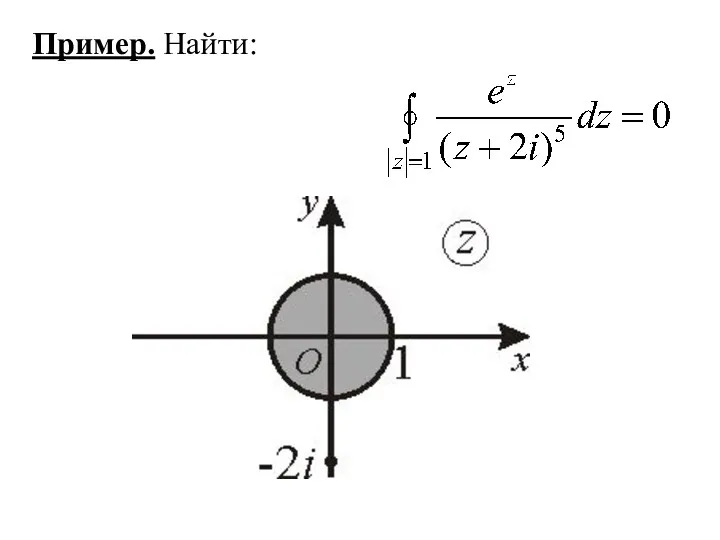
- 29. Пример. Найти:
- 49. Скачать презентацию














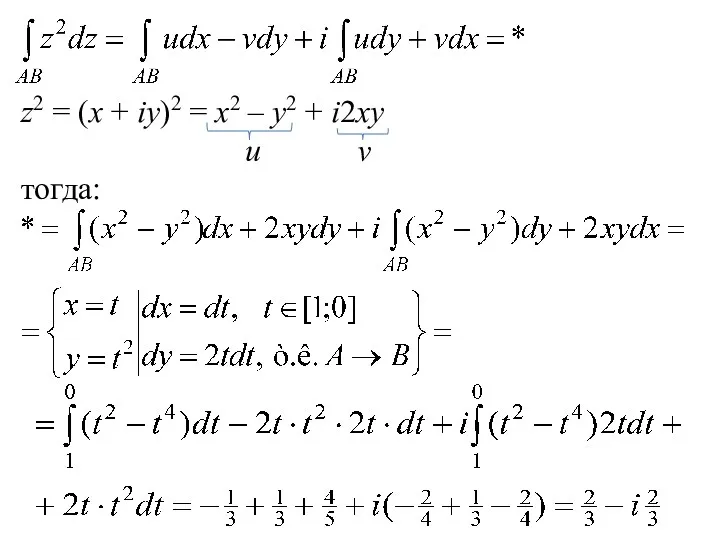




























 Проблемы юридической техники в уголовном праве
Проблемы юридической техники в уголовном праве Автоматизация звука Р
Автоматизация звука Р Теоретические основы товароведения продовольственных товаров
Теоретические основы товароведения продовольственных товаров Технология изготовления и монтаж деревянных лестниц. Устройство деревянного перекрытия
Технология изготовления и монтаж деревянных лестниц. Устройство деревянного перекрытия Способы организации пространства в ландшафтной архитектуре
Способы организации пространства в ландшафтной архитектуре Основы общественного производства
Основы общественного производства Процедура выбора страховой компании для строительной организации ООО Паркинг-М
Процедура выбора страховой компании для строительной организации ООО Паркинг-М Разработка технологии внесения растворов жидких комплексных удобрений (жку) в посевы сельскохозяйственных культур
Разработка технологии внесения растворов жидких комплексных удобрений (жку) в посевы сельскохозяйственных культур Традиционные общества востока
Традиционные общества востока Кошки
Кошки Христианин в труде
Христианин в труде День космонавтики.
День космонавтики. Порядок проверки и замены компрессора Dvm plus III
Порядок проверки и замены компрессора Dvm plus III 20231021_lyubit_svoego_podrostka_2012
20231021_lyubit_svoego_podrostka_2012 Ислам мәдениеті
Ислам мәдениеті Виды химической связи
Виды химической связи Деловая игра Знатоки ФГОС ДО
Деловая игра Знатоки ФГОС ДО Рейди мэйд в искусстве XX века
Рейди мэйд в искусстве XX века Роль воспитателя в процессе музык. воспитания
Роль воспитателя в процессе музык. воспитания образование в жизни человека
образование в жизни человека Моделирование и конструирование
Моделирование и конструирование Ознакомление детей дошкольного возраста с изобразительным искусством
Ознакомление детей дошкольного возраста с изобразительным искусством Проецирование. Проекция
Проецирование. Проекция Döwletleriň syýasy kartada şekillendirilşi
Döwletleriň syýasy kartada şekillendirilşi Современные способы обеззараживания воды
Современные способы обеззараживания воды Экономическая сущность предпринимательской деятельности
Экономическая сущность предпринимательской деятельности Эксплуатация системы кондиционирования воздуха пассажирских вагонов в пути следования
Эксплуатация системы кондиционирования воздуха пассажирских вагонов в пути следования Театр Моды Силуэт, коллекция Цвета жизни
Театр Моды Силуэт, коллекция Цвета жизни