Содержание
- 2. Ранее мы по данной функции вычисляли ее производную. Сегодня мы поставим обратную задачу: для данной функции
- 3. Определение. Функция называется первообразной функции если Примеры.
- 4. Таким образом, - это совокупность всех первообразных от данной функции. Определение 2. Пусть - одна из
- 5. Здесь называется подынтегральной функцией, а - подынтегральным выражением. Свойства
- 7. Таблица основных интегралов
- 8. Таблица основных интегралов
- 9. Таблица основных интегралов
- 10. Таблица основных интегралов
- 11. Таблица основных интегралов
- 12. Если то и Докажем справедливость формулы 3) Следовательно, для
- 13. Если то и Следовательно, для
- 14. Примеры.
- 25. Теорема. Любая непрерывная на отрезке функция имеет на этом отрезке первообразную. Действие отыскания неопределенного интеграла или,
- 26. Назовем график первообразной функции от интегральной кривой. Геометрический смысл неопределенного интеграла Таким образом, если то график
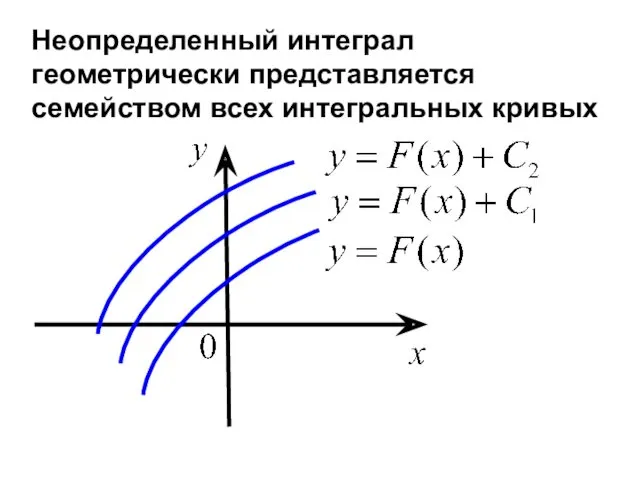
- 27. Неопределенный интеграл геометрически представляется семейством всех интегральных кривых
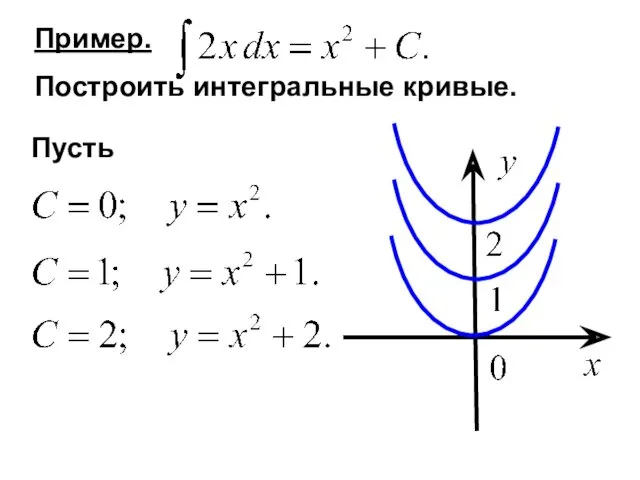
- 28. Пример. Построить интегральные кривые.
- 29. В дифференциальном исчислении производная от любой элементарной функции есть функция элементарная. Другое дело операция, обратная дифференцированию,
- 30. Можно привести примеры элементарных функций, первообразные от которых хотя и существуют, но не являются элементарными функциями.
- 31. Несмотря на это, все эти первообразные хорошо изучены и для них составлены таблицы, помогающие практически использовать
- 32. Эта функция встречается в теории вероятностей и называется интегралом вероятностей. Если первообразная для некоторой функции не
- 33. Тема: Замена переменной в неопределенном интеграле
- 34. Введем вместо новую переменную связанную с соотношением Тогда
- 35. Примеры.
- 37. Имеем
- 38. Здесь мы устно ввели под знак интеграла функцию Заметим, что
- 39. Замечая, что получаем
- 40. 4) Интегралы вида Эти интегралы вычисляются методом разложения на основании тригонометрических тождеств.
- 43. Можно устно внести под знак дифференциала: Тогда
- 44. Рассмотрим три способа. ② ①
- 45. Проверка. ③
- 49. Скачать презентацию




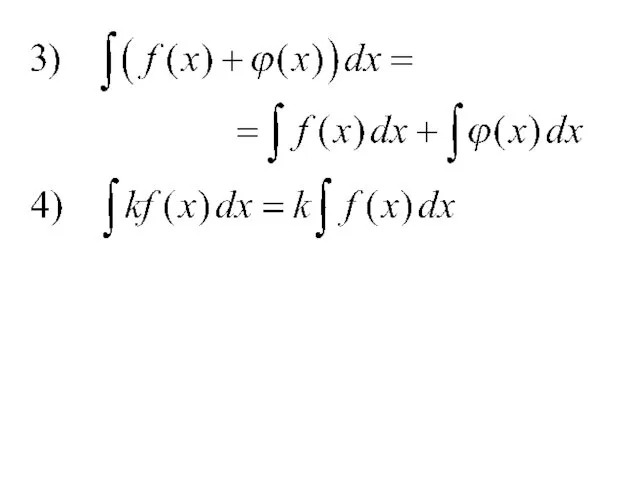






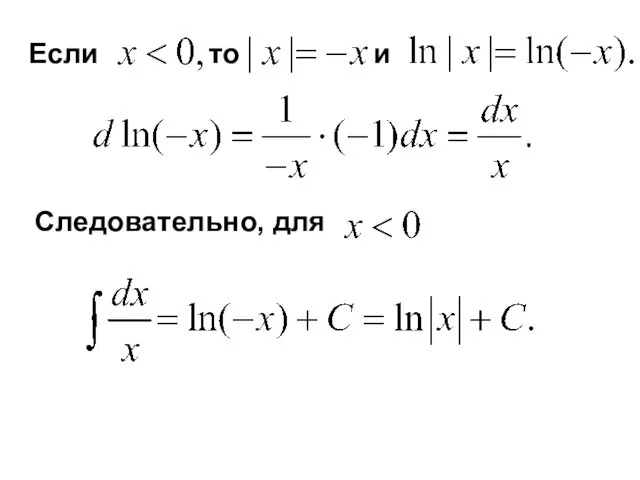
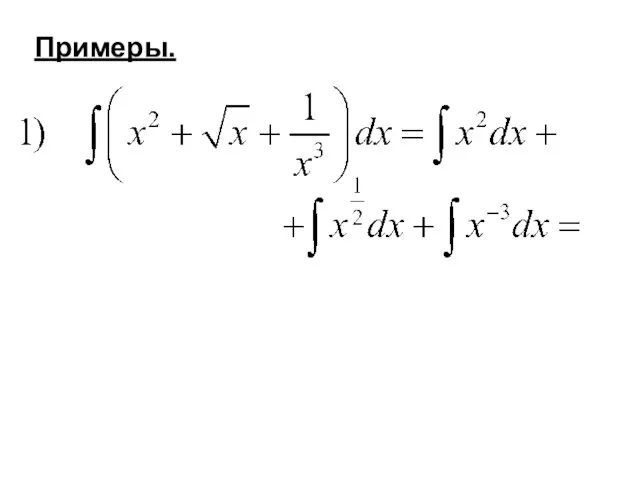
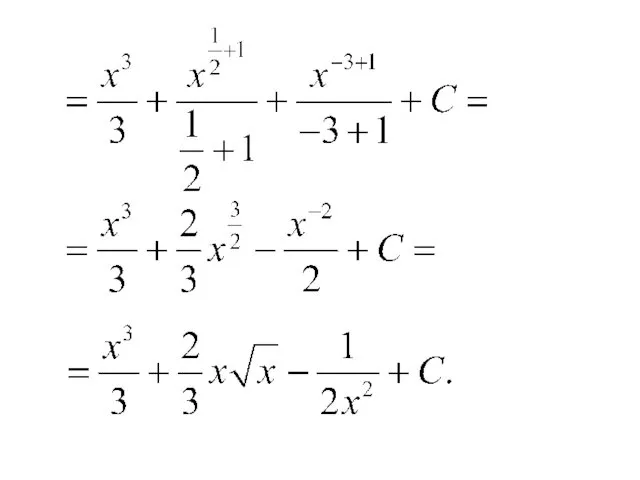
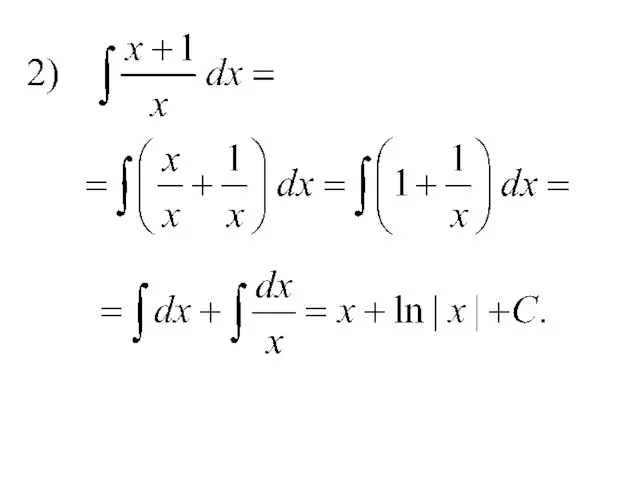
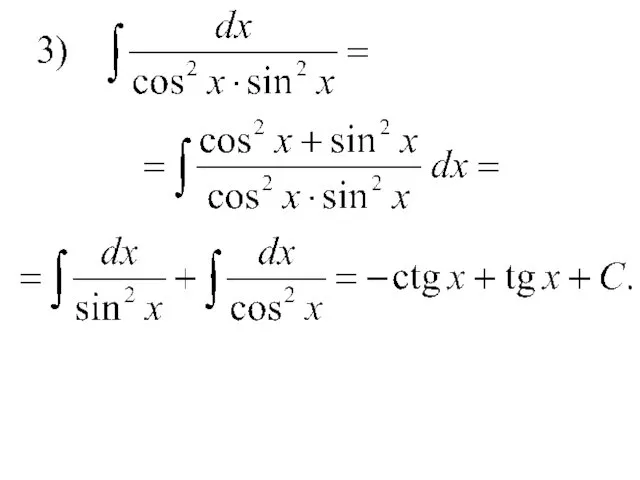
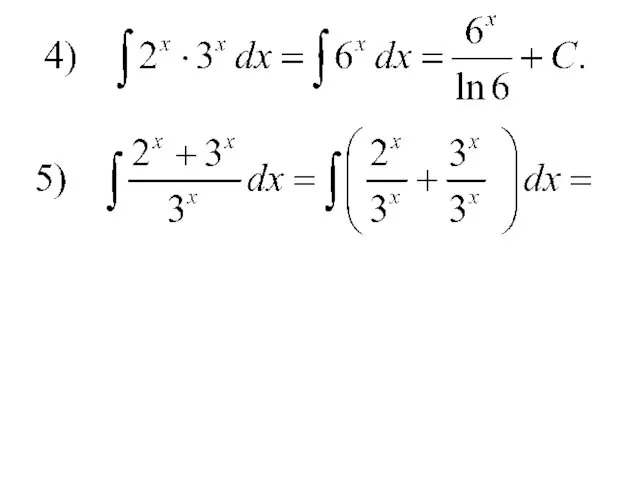
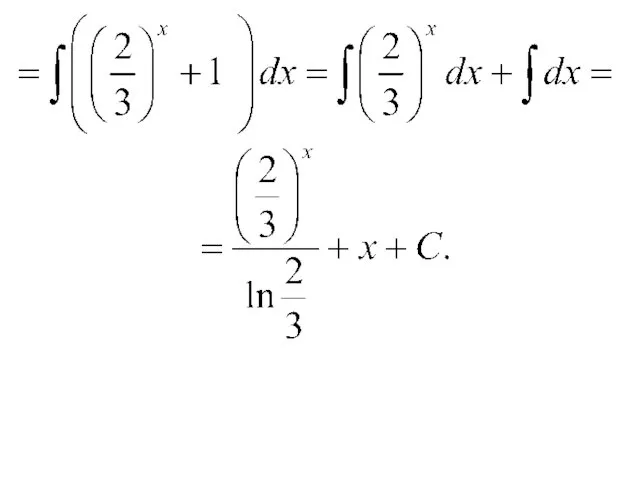
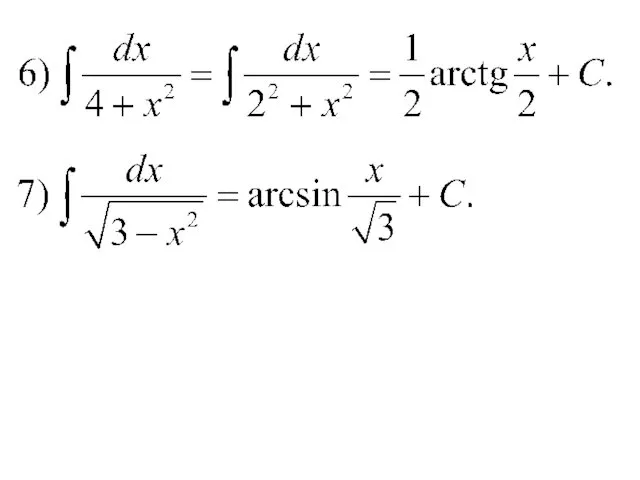
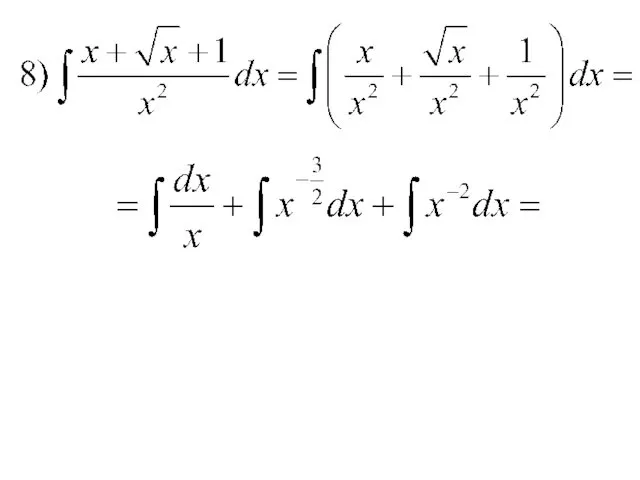
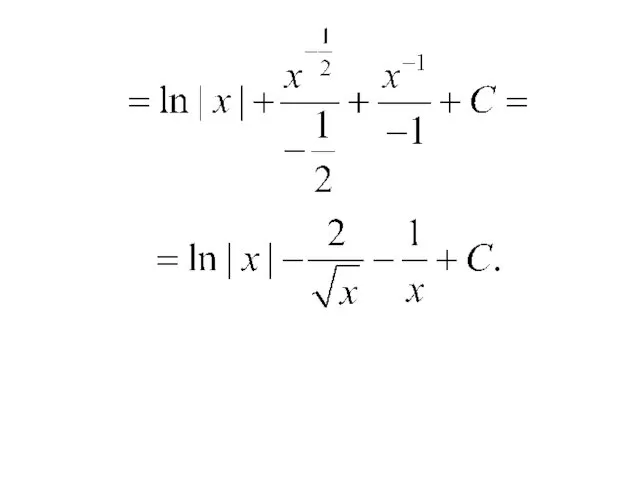
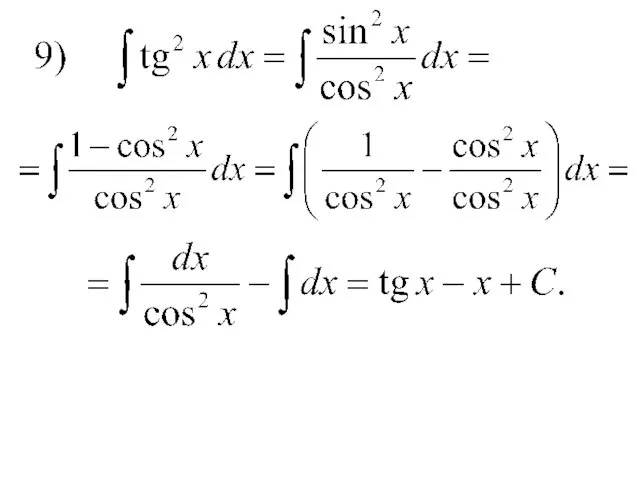
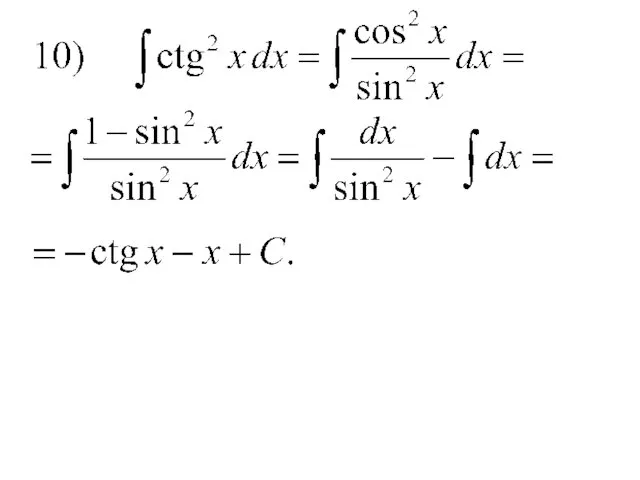








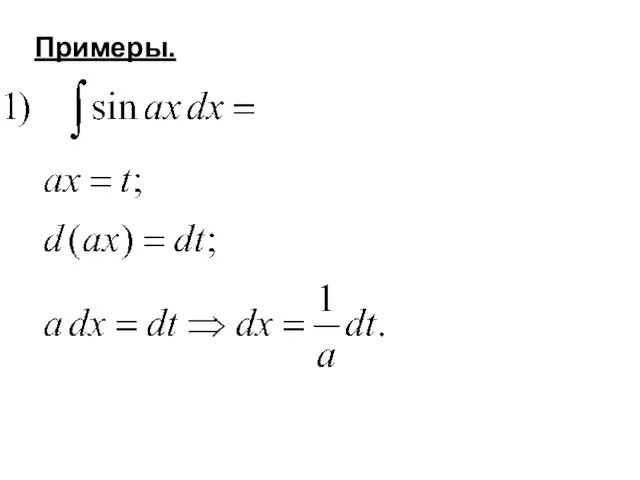
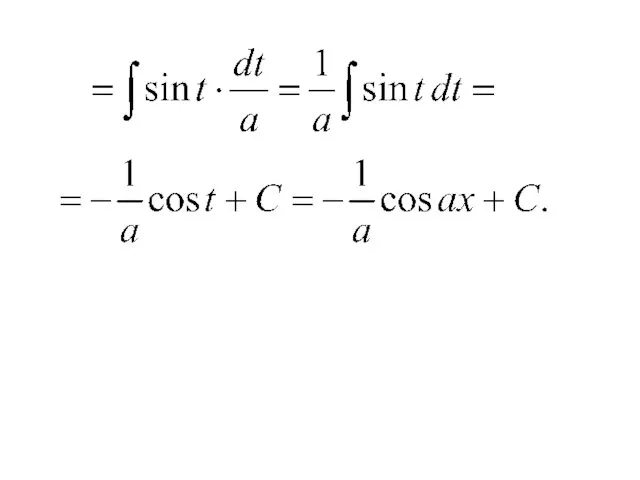
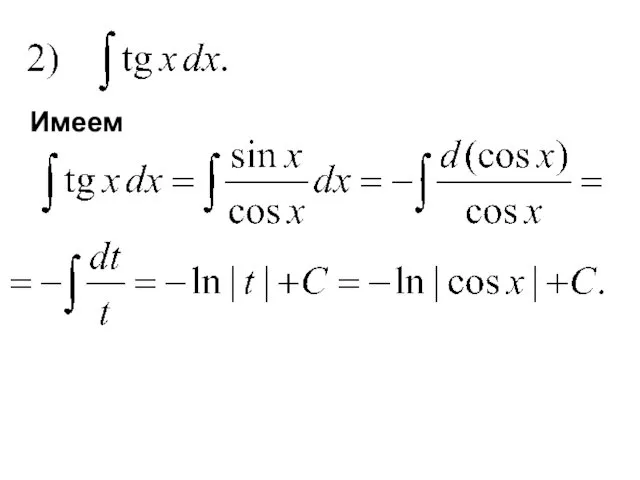

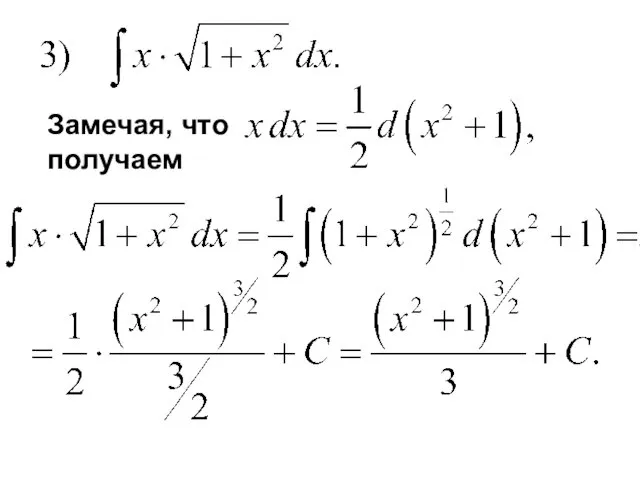

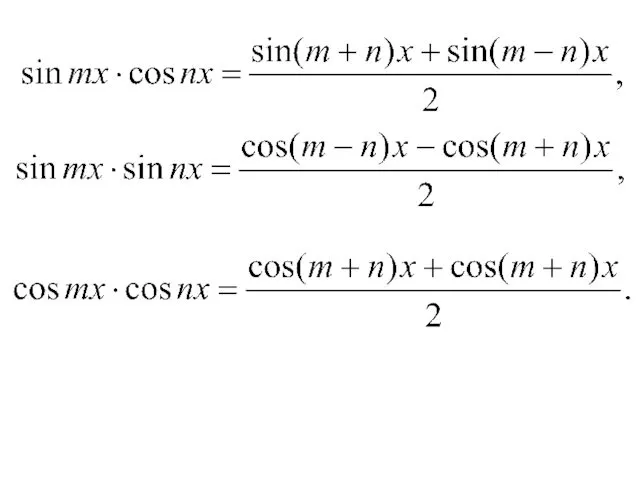
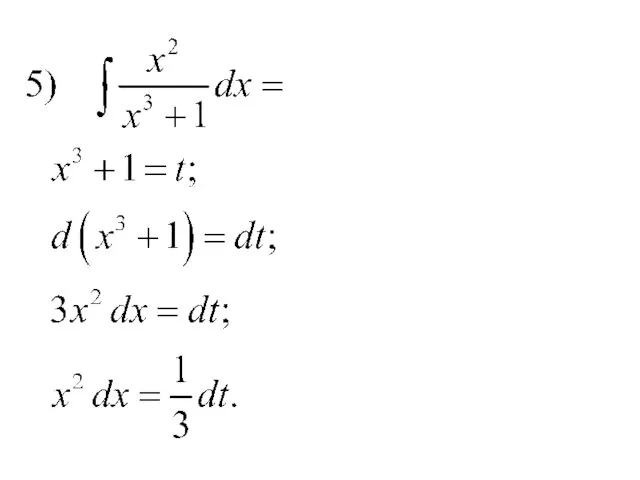

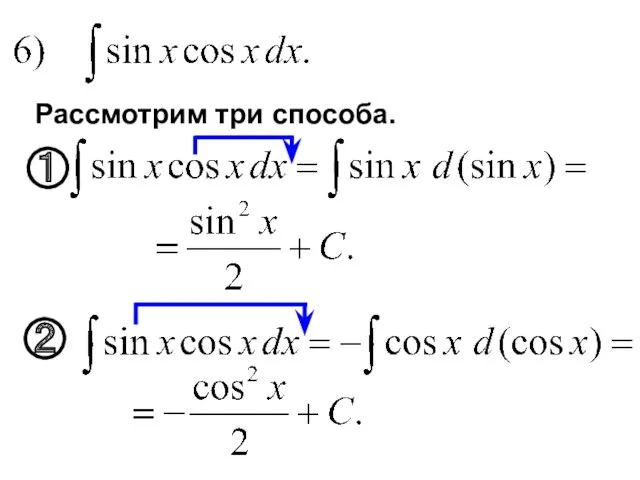
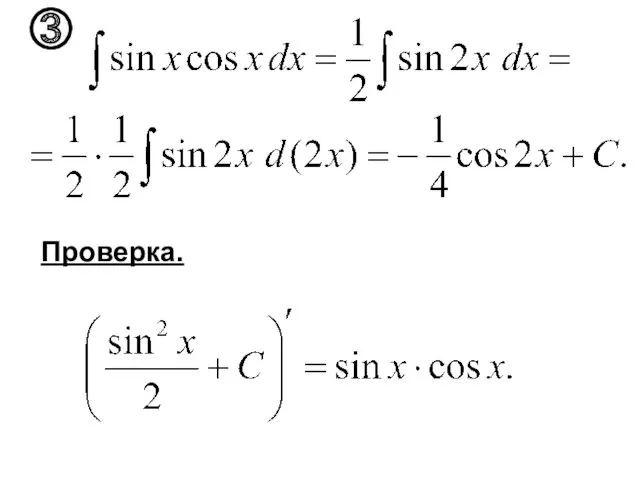
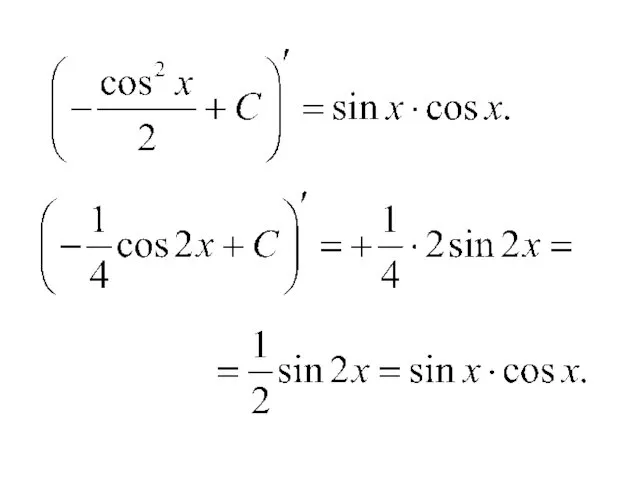
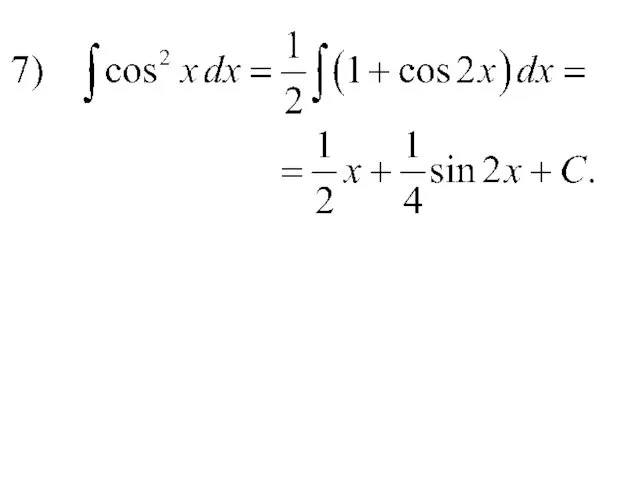
 Канализация схемалары және оның негізгі элементтері
Канализация схемалары және оның негізгі элементтері Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Сказочные истории
Сказочные истории Конус. Виды конусов
Конус. Виды конусов 1-е и 2-е Послания к Коринфянам. Общие сведения
1-е и 2-е Послания к Коринфянам. Общие сведения Физкультминутка Веселые снеговики
Физкультминутка Веселые снеговики Презентация Книжные уголки Солнечной полянки
Презентация Книжные уголки Солнечной полянки Игра -это серьезно
Игра -это серьезно 20231101_diktant_proizvodnaya_4_var
20231101_diktant_proizvodnaya_4_var Управление информационными ресурсами. Лекция 1
Управление информационными ресурсами. Лекция 1 Коллигативные свойства растворов. Лекция 2
Коллигативные свойства растворов. Лекция 2 Отравляющие вещества. Яды природного и техногенного происхождения
Отравляющие вещества. Яды природного и техногенного происхождения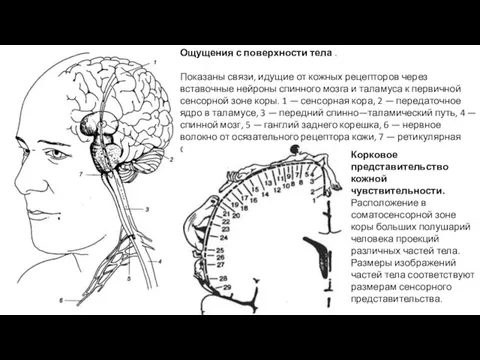 Ощущения с поверхности тела
Ощущения с поверхности тела История возникновения городов Западной Европы в их названиях
История возникновения городов Западной Европы в их названиях журнал№2;1;3
журнал№2;1;3 Всемирный день ориентирования
Всемирный день ориентирования Проект Разнообразие природы родного края, 3 класс
Проект Разнообразие природы родного края, 3 класс Развитие телефона
Развитие телефона Презентация Патриоты России.
Презентация Патриоты России. Постпозитивістські концепції в бухгалтерських наукових дослідженнях
Постпозитивістські концепції в бухгалтерських наукових дослідженнях Симметричное и ассиметричное шифрование
Симметричное и ассиметричное шифрование Школьникова Т.Ю. СОШ №5
Школьникова Т.Ю. СОШ №5 Занимательная грамматика.
Занимательная грамматика. Поняття про свердловину
Поняття про свердловину Русская Классическая Школа педагогическая стратегия будущего, проверенная великим образовательным прошлым
Русская Классическая Школа педагогическая стратегия будущего, проверенная великим образовательным прошлым ДопускКпеддеят.ОткрУрок03.12.2020
ДопускКпеддеят.ОткрУрок03.12.2020 10 заповедей родителям
10 заповедей родителям Портфолио учителя
Портфолио учителя