Содержание
- 2. Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Предел суммы (разности) двух функций
- 3. Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя
- 4. Формулы 1) lim 1/n = 0 n→∞ 2) lim qn = 0, если 0 n→∞ Если
- 5. Правила вычисления пределов Если lim хn = b и lim уn = c , то n→∞
- 6. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 7. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 8. Раскрытие неопределенностей Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель
- 9. Раскрытие неопределенностей Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить числитель и
- 10. Пример. Вычислить Решение. Делим числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n,
- 11. Раскрытие неопределенностей Умножим и разделим функцию на сопряженное выражение.
- 12. Первый замечательный предел Следствия: Формула справедлива также при x
- 14. Скачать презентацию











 С днем мамы
С днем мамы Семья пастора
Семья пастора Комплексные числа
Комплексные числа ФГОС в дошкольном образовании
ФГОС в дошкольном образовании Пластиковые окна или старые деревянные
Пластиковые окна или старые деревянные Битва под Сталинградом
Битва под Сталинградом Устный журнал Путешествие по планете Памяти
Устный журнал Путешествие по планете Памяти Бойове застосування КЗА 86Ж6. Алгоритми обробки радiолокацiйної iнформацiї, виявлення та захоплення цiлей. (Тема 8.3)
Бойове застосування КЗА 86Ж6. Алгоритми обробки радiолокацiйної iнформацiї, виявлення та захоплення цiлей. (Тема 8.3) Саванны. Субэкваториальный климатический пояс
Саванны. Субэкваториальный климатический пояс Воспитательная система класса
Воспитательная система класса Презентация Семья и школа в формировании личности ребенка
Презентация Семья и школа в формировании личности ребенка Clothes and Fashion
Clothes and Fashion Ограничение облучения от природных источников
Ограничение облучения от природных источников Презентация к викторине У сказки тихий голосок.
Презентация к викторине У сказки тихий голосок. Сюжетно-ролевая игра
Сюжетно-ролевая игра Мастер моего села
Мастер моего села Блиц-опрос Я знаю лес
Блиц-опрос Я знаю лес Концепция педагогической деятельности
Концепция педагогической деятельности System administracji publicznej w Hondurasie
System administracji publicznej w Hondurasie GP USB DownLoad Manual (English_Version)
GP USB DownLoad Manual (English_Version)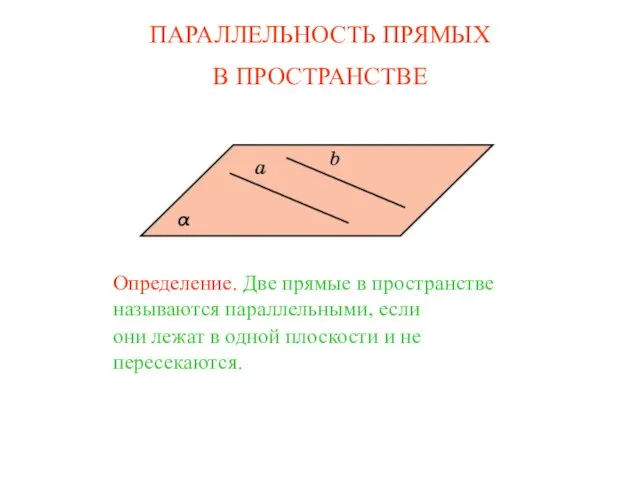 Параллельность прямых в пространстве
Параллельность прямых в пространстве Хранение дел организации. (Тема 4)
Хранение дел организации. (Тема 4) Формирование комфортной городской среды
Формирование комфортной городской среды PML30_SummerPractice2022_Presentation_Pattern
PML30_SummerPractice2022_Presentation_Pattern Декоративный пейзаж
Декоративный пейзаж Пищевая сода. Необычное в обычном
Пищевая сода. Необычное в обычном Как научить своего ребёнка жить в мире людей. Уроки этики поведения для детей и родителей
Как научить своего ребёнка жить в мире людей. Уроки этики поведения для детей и родителей Выдающиеся открытия в области химии
Выдающиеся открытия в области химии