Содержание
- 2. Цель лекции – ознакомится с предметом и основными понятиями комбинаторного анализа
- 3. Литература Глускин Л.М., Шор Л.А., Шварц В.Я. Задачи и алгоритмы комбинаторики, и теории графов. Донецк, ДПИ,
- 4. Базовые понятия: Множество Подмножество Упорядоченность Мощность Факториал Термины Ключевые слова: Перестановка Подстановка Инверсия Четность подстановки Цикл
- 5. Комбинаторный анализ как раздел дискретной математики Во многих математических исследованиях встречаются комбинаторные задачи – задачи выбора
- 6. Комбинаторный анализ как раздел дискретной математики Без учета влияния случайных явлений человек становится бессильным направлять развитие
- 7. Комбинаторный анализ как раздел дискретной математики Комбинаторика занимается различного рода сочетаниями (соединениями), которые можно образовать из
- 8. Комбинаторный анализ как раздел дискретной математики Как научная дисциплина комбинаторика сформировалась лишь в XVII веке. Термин
- 9. Правило суммы Теоретико-множественная формулировка: пусть конечное множество М представлено объединением попарно непересекающихся подмножеств M1, M2, …,
- 10. Правило суммы: пример Из Харькова в Киев в течение суток отправляются 6 поездов, 4 автобуса и
- 11. Правило произведения Теоретико-множественная формулировка: пусть M1, M2, …, Mn – конечные множества, М=М1×М2×…×Mn – их декартово
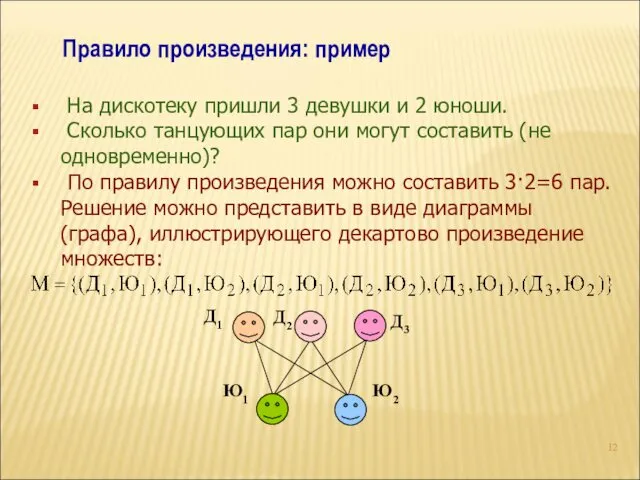
- 12. Правило произведения: пример На дискотеку пришли 3 девушки и 2 юноши. Сколько танцующих пар они могут
- 13. Перестановки Пусть М – конечное множество, состоящее из n элементов. Они могут быть перенумерованы при помощи
- 14. Пример Числа 1, 2, 3 можно расположить следующими способами: 1, 2, 3 1, 3, 2 2,
- 15. Количество перестановок из n элементов Перестановки из n элементов множества M отличаются друг от друга только
- 16. Подстановки Def: взаимно-однозначное отображение πn конечного упорядоченного множества M={s1,s2,…,sn} из n элементов на себя называется подстановкой
- 17. Тождественная подстановка Def: подстановка, при которой на месте остаются все элементы, называется тождественной: Все точки тождественной
- 18. Произведение подстановок Пусть M={1,2,…,n} – произвольное множество, πn – подстановка элементов множества M: где {s1,s2,…,sn} –
- 19. Time-Out
- 20. Пример Найти произведение подстановок: и Решение: Определим произведение в обратном порядке:
- 21. Совместимость подстановок Def: подстановки одинаковых степеней называются совместимыми. Можно перемножать только совместимые подстановки. Умножение подстановок n-й
- 22. Симметрическая группа подстановок 1. Для любых двух подстановок из n элементов множества М произведение есть однозначно
- 23. Пример симметрической группы подстановок Элементы симметрической группы S3 определяются как:
- 24. Инверсии. Четность подстановки Def: если в матрице подстановки πn элементов множества M={1,2,…n} встречаются два столбца для
- 25. Упражнение Определить четность подстановок симметрической группы S3
- 26. Подстановки с циклами Если матрицу подстановки πn перестановкой столбцов можно привести к виду , то πn
- 27. Пример Представить подстановки в виде разложения на независимые циклы:
- 28. Перестановки с повторениями. 1 Дано множество М, состоящее из n элементов. Требуется представить множество М в
- 29. Перестановки с повторениями. 2 Теорема. Пусть k1, k2, …, km – натуральные числа такие, что k1+k2+…+km
- 31. Скачать презентацию



























 Внеурочная деятельность. Нормативно-правовая база внеурочной деятельности
Внеурочная деятельность. Нормативно-правовая база внеурочной деятельности Порядок назначения и выплаты социальных стипендий
Порядок назначения и выплаты социальных стипендий Family members
Family members Системно-деятельностный подход в обучении младших школьников
Системно-деятельностный подход в обучении младших школьников Отряд ЮИД школы №500 представляет Внимание - ДЕТИ!!!
Отряд ЮИД школы №500 представляет Внимание - ДЕТИ!!! Литература Древней Руси IX-XII веков
Литература Древней Руси IX-XII веков Приоритеты развития экономики России и влияние экономической науки на ход экономических реформ
Приоритеты развития экономики России и влияние экономической науки на ход экономических реформ Участия в окружном и краевом конкурсе Пою мое Отечество, посвященненные 70-летию Дня Победы.
Участия в окружном и краевом конкурсе Пою мое Отечество, посвященненные 70-летию Дня Победы. Гражданская война в России
Гражданская война в России Эволюция науки муниципального права в России (советский период)
Эволюция науки муниципального права в России (советский период) Жизнь дана на добрые дела
Жизнь дана на добрые дела Железнодорожный путь, изыскание и проектирование железных дорог
Железнодорожный путь, изыскание и проектирование железных дорог Объем и скорость передачи цифрового потока ТВ-информации. Резервы сокращения цифрового потока ТВ-систем. (Лекция 5)
Объем и скорость передачи цифрового потока ТВ-информации. Резервы сокращения цифрового потока ТВ-систем. (Лекция 5) Витраж в современном дизайне интерьера
Витраж в современном дизайне интерьера Изменения свойств химических элементов и их соединений в периодах
Изменения свойств химических элементов и их соединений в периодах Основные обязанности специалиста отдела IT
Основные обязанности специалиста отдела IT занятие по развитию речи Цветы Диск
занятие по развитию речи Цветы Диск Инновационный интегрированный предмет Краеведение
Инновационный интегрированный предмет Краеведение Systemy transportowe – transport globalny
Systemy transportowe – transport globalny Сущность предварительно напряженного железобетона
Сущность предварительно напряженного железобетона Путешествие в Грецию. Остров Крит
Путешествие в Грецию. Остров Крит Роль игры в развитии ребенка
Роль игры в развитии ребенка Политология, как наука
Политология, как наука Максимилиан Александрович Волошин (1877-1932) – русский поэт серебряного века, художник, критик
Максимилиан Александрович Волошин (1877-1932) – русский поэт серебряного века, художник, критик классный час ЗОЖ
классный час ЗОЖ Технология VLSM. Маски подсети переменной длины
Технология VLSM. Маски подсети переменной длины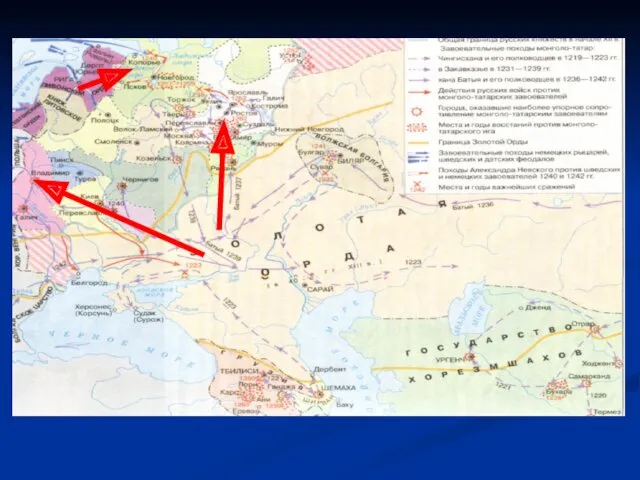 Борьба Руси с западными завоевателями в XIII веке
Борьба Руси с западными завоевателями в XIII веке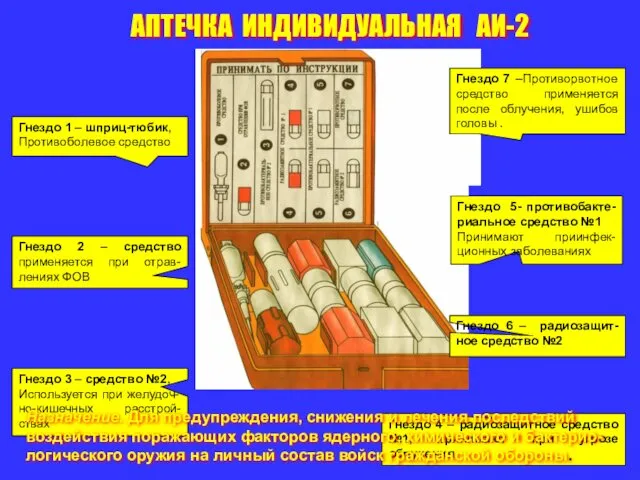 Аптечка индивидуальная АИ-2
Аптечка индивидуальная АИ-2