Содержание
- 2. Логика финансовых вычислений. Финансовая математика изучает методы и методики определения стоимостных и вре- менных параметров финансовых
- 3. Методы финансовой математики чаще всего применяют при решении следующих практических задач: вычисление конечных сумм, находящихся во
- 4. К внутренним факторам относя те факторы, которые определяют: основные характеристики финансового процесса; контрактные характеристики сделки (
- 5. 2. Формула наращения. В основе финансовой математики лежит понятие временной стоимости, т.е. принцип неравноценности денег, относящихся
- 6. Процесс, в котором по первоначальной сумме и процентной ставке необходимо найти ожидаемую в будущем к получению
- 7. Примем обозначения: I – проценты за весь срок ссуды P – первоначальная сумма S – наращенная
- 8. Ставка наращения процентов «i» определяется отношением процентных денег к величине первоначального капитала, т.е. Ставку наращения процентов
- 9. Множитель ( 1 + ni ) называют множителем наращения простых процентов. Пример. Вкладчик положил в банк,
- 10. 3. Практика расчета процентов для краткосрочных ссуд. Так как процентная ставка, как правило, устанавливается в расчете
- 11. На практике используют три варианта расчета простых процентов: 1. Английский: точные проценты с точным числом дней
- 12. Пример. Ссуда в размере 500000 руб. выдана 20 января до 5 октября включительно под 18% го-
- 13. 365/365 – точные проценты с точным числом дней ссуды 365/360 – обыкновенные проценты с точным числом
- 14. 4. Переменные ставки. В условиях меняющегося состояния финансового рынка при заключении финансового соглашения может быть установлена
- 15. S = P + Pn1i1 + Pn2i2 +……+ Pnmim = P ( 1 + n1i1 +
- 16. 5. Реинвестирование по простым процентам. Если по истечении некоторого периода зафиксированная к данному моменту наращен- ная
- 17. Таким образом, итоговую наращенную сумму определяют по формуле: P ( 1 + n1i1 ) ( 1
- 18. Решение Если начислять точные проценты ( 365/365 ), то Если начислять обыкновенные проценты ( 360/360 ),
- 19. Решение Р = 500000 руб., n1 = 1 месяц = 1/12 i1 = 0,1, n2 =
- 20. Для решения этой задачи применяют операцию дисконтирования. Дисконтирование позволяет по известным значениям наращенной суммы, процент- ной
- 21. Рассмотрим, как проводят математическое дисконтирование. Выразив из формулы S = P(1 + ni) величину P, получим
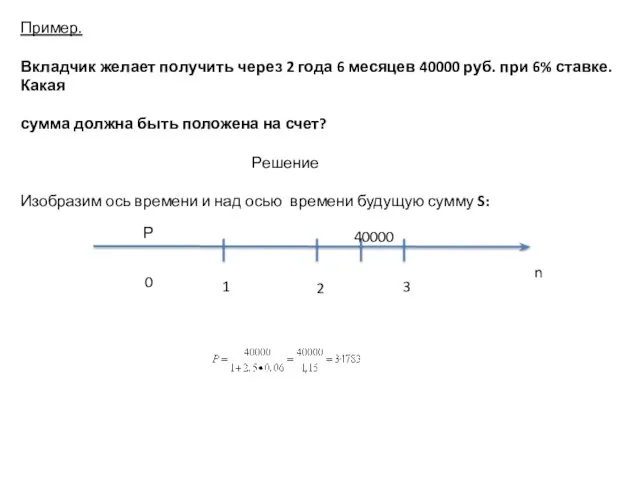
- 22. Пример. Вкладчик желает получить через 2 года 6 месяцев 40000 руб. при 6% ставке. Какая сумма
- 23. Операцию предварительного начисления процентов называют дисконтированием по учетной ставке, или банковским ( коммерческим ) учетом. Это
- 24. Пример. Кредит в 7000 руб. Выдается на 0,5 года по простой учетной ставке 11% годовых. Какую
- 25. Цена Р рассчитывается по формуле: P = S – Snd = S ( 1 – nd
- 26. Решение S = 50000 руб., n = 2, d = 8% Р = S ( 1
- 27. ( при n = 1/d ) или даже становится отрицательной (n > 1/d ). Понятно, что
- 29. Скачать презентацию

























 Основы педагогического мастерства и Формирование информационной компетентности участников образовательного процесса
Основы педагогического мастерства и Формирование информационной компетентности участников образовательного процесса Coca-Cola Format Template
Coca-Cola Format Template Учимся жить дружно
Учимся жить дружно Приемы устного счета
Приемы устного счета Тиристоры
Тиристоры Биогаз - экологически чистое топливо
Биогаз - экологически чистое топливо Районный семинар школьных библиотекарей
Районный семинар школьных библиотекарей Уголовная ответственность несовершеннолетних
Уголовная ответственность несовершеннолетних Виртуальная экскурсия на Соколовую гору г.Саратова
Виртуальная экскурсия на Соколовую гору г.Саратова Татар теле 4 класс
Татар теле 4 класс Процессы в неживой природе. 6 класс
Процессы в неживой природе. 6 класс МАИ – ведущий аэрокосмический вуз России
МАИ – ведущий аэрокосмический вуз России Паспорт мини-музея Хлеба
Паспорт мини-музея Хлеба Работа с одарёнными детьми
Работа с одарёнными детьми Обеспечение и поддержание инфекционной безопасности при выполнении трудовых действий
Обеспечение и поддержание инфекционной безопасности при выполнении трудовых действий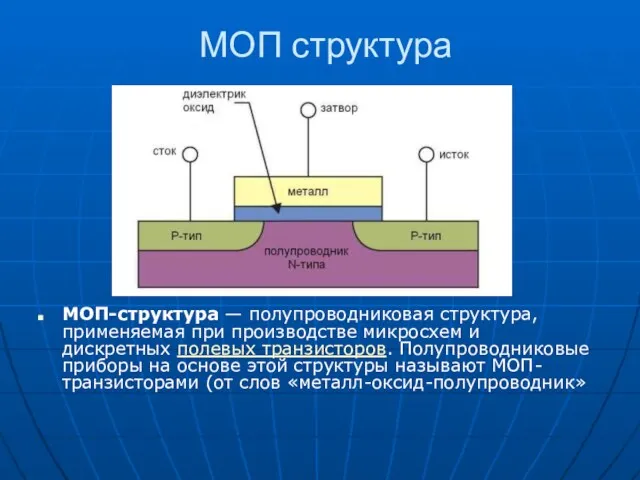 МОП и КМОП структуры
МОП и КМОП структуры Профессиональный стресс. Проявление хронической усталости и психического выгорания
Профессиональный стресс. Проявление хронической усталости и психического выгорания Моя семья
Моя семья Калібрування аналогових вольтметрів (тема № 2, заняття № 1)
Калібрування аналогових вольтметрів (тема № 2, заняття № 1) Симптомы и методы обследования в пульмонологии
Симптомы и методы обследования в пульмонологии Проблемы реализации принципа презумпции невиновности на досудебных стадиях
Проблемы реализации принципа презумпции невиновности на досудебных стадиях Урок развития речи в 6 классе
Урок развития речи в 6 классе Устройство компьютера
Устройство компьютера Здоровый образ жизни
Здоровый образ жизни Как заставить себя учиться
Как заставить себя учиться Основные составляющие шрифта
Основные составляющие шрифта The Martian
The Martian Препроцессор. Роль препроцессора при компиляции программы
Препроцессор. Роль препроцессора при компиляции программы