Содержание
- 2. План презентации: Определение сферы, шара. Уравнение сферы. Взаимное расположение сферы и плоскости. Площадь сферы. Итог урока.
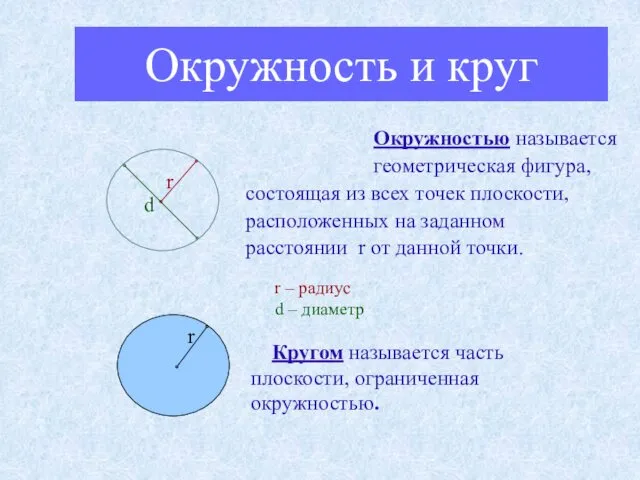
- 3. Окружность и круг Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии
- 4. Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от
- 5. Шар Шаром называется тело, ограниченное сферой. Центр, радиус и диаметр сферы являются также центром, радиусом и
- 6. Как изобразить сферу? 1. Отметить центр сферы (т.О) 2. Начертить окружность с центром в т.О 3.
- 7. Уравнение окружности О С(х0;у0) М(х;у) Зададим прямоугольную систему координат Оxy Построим окружность c центром в т.
- 8. Уравнение сферы Зададим прямоугольную систему координат Оxyz z х у М(х;у;z) R C(x0;y0;z0) Построим сферу c
- 9. Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы. Решение: так как
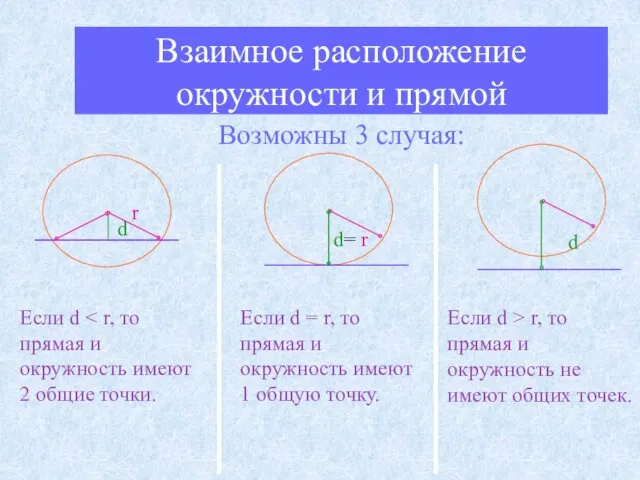
- 10. Взаимное расположение окружности и прямой Возможны 3 случая: d d r Если d d= r Если
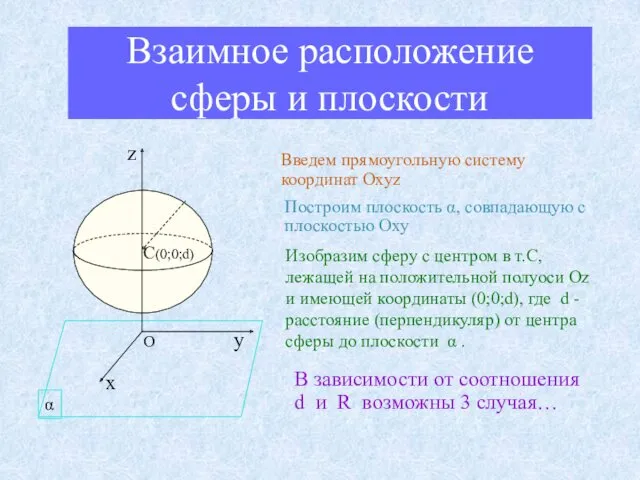
- 11. Взаимное расположение сферы и плоскости Введем прямоугольную систему координат Oxyz Построим плоскость α, совпадающую с плоскостью
- 12. Взаимное расположение сферы и плоскости r М Рассмотрим 1 случай: d r = R2 - d2
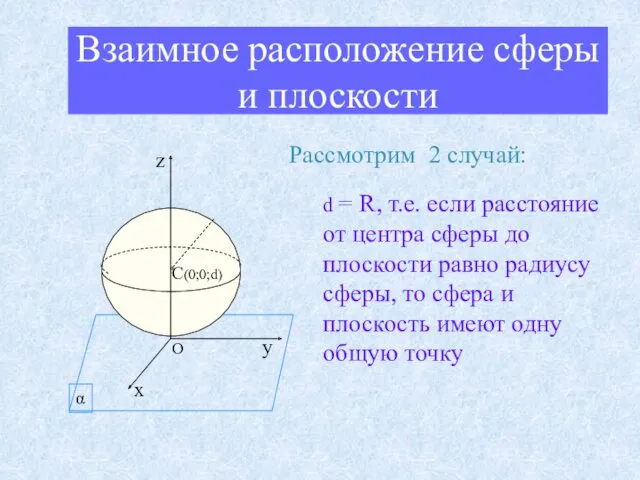
- 13. Взаимное расположение сферы и плоскости Рассмотрим 2 случай: d = R, т.е. если расстояние от центра
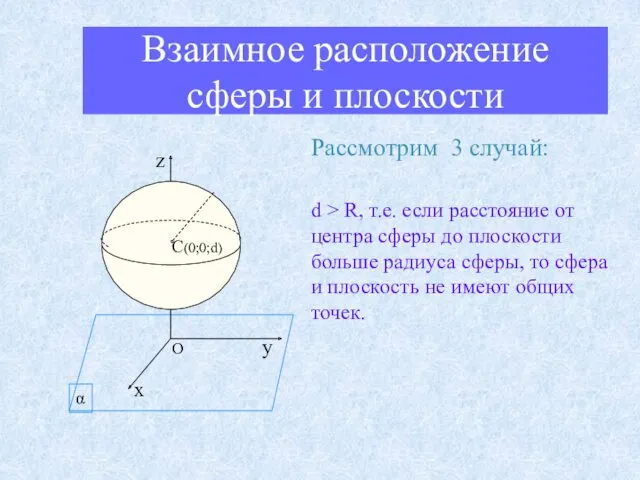
- 14. Взаимное расположение сферы и плоскости Рассмотрим 3 случай: d > R, т.е. если расстояние от центра
- 15. Задача 2. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти
- 16. Площадь сферы и шара Сферу нельзя развернуть на плоскость. Опишем около сферы многогранник, так чтобы сфера
- 17. Задача 3. Найти площадь поверхности сферы, радиус которой равен 6 см. Дано: сфера R = 6
- 19. Скачать презентацию











 Штамповые испытания нежестких дорожных конструкций
Штамповые испытания нежестких дорожных конструкций Развивающая среда во 2младшей группе.
Развивающая среда во 2младшей группе. Компьютер – основной инструмент подготовки текстов
Компьютер – основной инструмент подготовки текстов Внеклассная работа учителя начальных классов
Внеклассная работа учителя начальных классов Материал урока Электролитическая диссоциация
Материал урока Электролитическая диссоциация Removing 6634 UEPP
Removing 6634 UEPP Мой дом-моя семья. Материал для родителей.
Мой дом-моя семья. Материал для родителей. Рэфармацыя і цывілізацыя
Рэфармацыя і цывілізацыя bcd067371120e27b50dcb49e8
bcd067371120e27b50dcb49e8 Воспитательная программа
Воспитательная программа Смысл жизни. Виктор Франкл. (Тема 7)
Смысл жизни. Виктор Франкл. (Тема 7)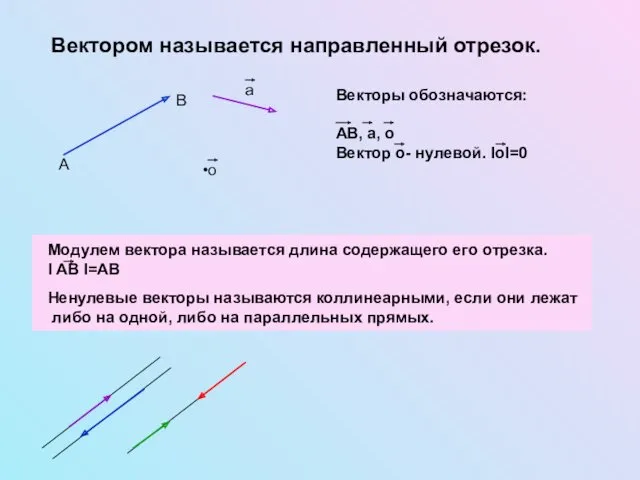 Вектор
Вектор 第八课 Урок 8
第八课 Урок 8 Понятие основ конституционного строя России
Понятие основ конституционного строя России Хроническое легочное сердце
Хроническое легочное сердце Центральная и Восточная Европа
Центральная и Восточная Европа Флористическое оформление витрин в стиле барокко
Флористическое оформление витрин в стиле барокко О реализации мероприятий Формирование комфортной городской среды на территории Волховского муниципального района
О реализации мероприятий Формирование комфортной городской среды на территории Волховского муниципального района Математика 31
Математика 31 Дикие животные
Дикие животные Букет для мамы
Букет для мамы Электрохимические методы. Продолжение. Лекция 10
Электрохимические методы. Продолжение. Лекция 10 Отчет по производственной практике. Архитектура
Отчет по производственной практике. Архитектура Портфолио по профессиональному модулю ПМ.01 Эксплуатация и модификация информационных систем
Портфолио по профессиональному модулю ПМ.01 Эксплуатация и модификация информационных систем Презентация к викторине по творчеству И.С.Тургенева
Презентация к викторине по творчеству И.С.Тургенева Қара бидай мен тритикале сұрыптық ұнға дайындау принциптері
Қара бидай мен тритикале сұрыптық ұнға дайындау принциптері Здоровьесберегающие технологии в системе оздоровительной работы ДОУ согласно требованиям ФГОС
Здоровьесберегающие технологии в системе оздоровительной работы ДОУ согласно требованиям ФГОС Электроэнергетика России
Электроэнергетика России