Содержание
- 2. Статическая и динамическая устойчивость Статическая устойчивость ??? Устойчивость в малом. Устойчивость при малых возмущениях. Применительно к
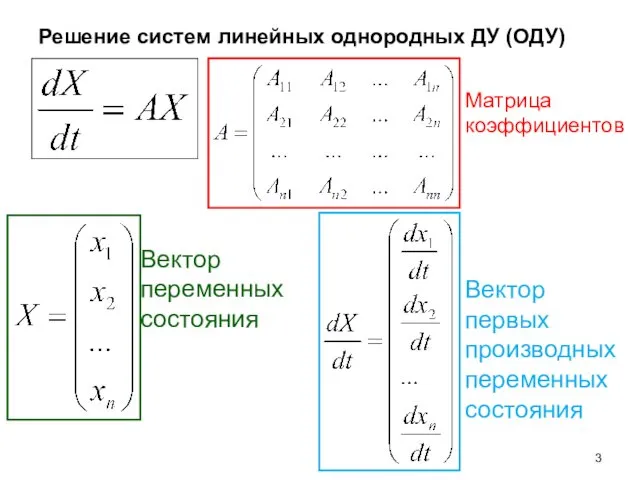
- 3. Решение систем линейных однородных ДУ (ОДУ) Матрица коэффициентов Вектор переменных состояния Вектор первых производных переменных состояния
- 4. Решение систем линейных ОДУ Решение системы ОДУ ищется в следующем виде:
- 5. Собственные числа и вектора Собственный вектор матрицы – вектор, умножение матрицы на который дает тот же
- 6. Поиск собственных чисел и векторов A – матрица ОДУ; N – собственный вектор; λ – собственное
- 7. Решение систем линейных ОДУ
- 8. Устойчивость системы линейных ОДУ Линейная система устойчива, если все собственные числа имеют отрицательные действительные части. Линейная
- 9. Анализ устойчивости системы нелинейных ДУ Матрица Якоби Якобиан
- 10. Устойчивость системы НЕлинейных ДУ Если все собственные значения якобиана имеют отрицательные действительные части, то нулевое решение
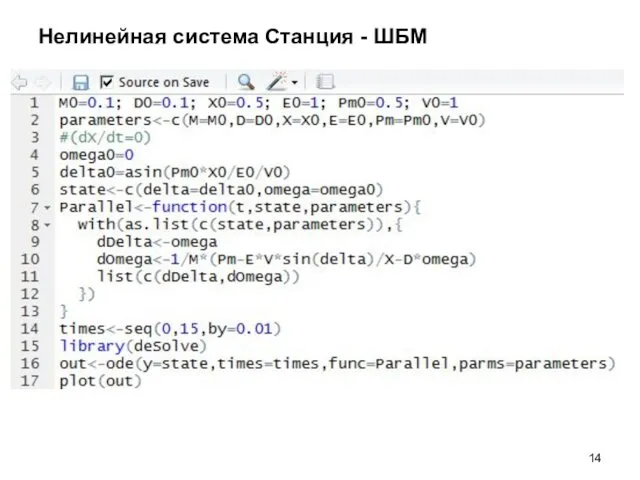
- 11. Нелинейная система Станция - ШБМ
- 12. Нелинейная система Станция - ШБМ
- 13. Анализ собственных чисел системы ШБМ Проведем анализ на тестовой схеме со следующими параметрами: M0=0.1; D0=0.1; X0=0.5;
- 14. Нелинейная система Станция - ШБМ
- 15. Анализ статической устойчивости ШБМ δ≡π/2 – точка, отделяющая состояния устойчивого и неустойчивого равновесий. При δ≡π/2 Pm0max
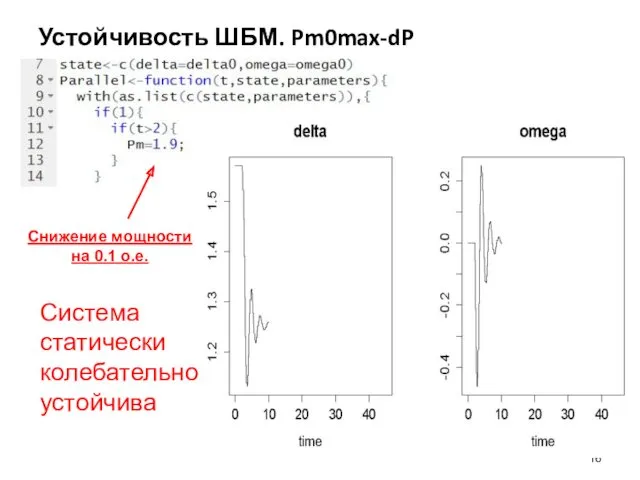
- 16. Устойчивость ШБМ. Pm0max-dP Снижение мощности на 0.1 о.е. Система статически колебательно устойчива
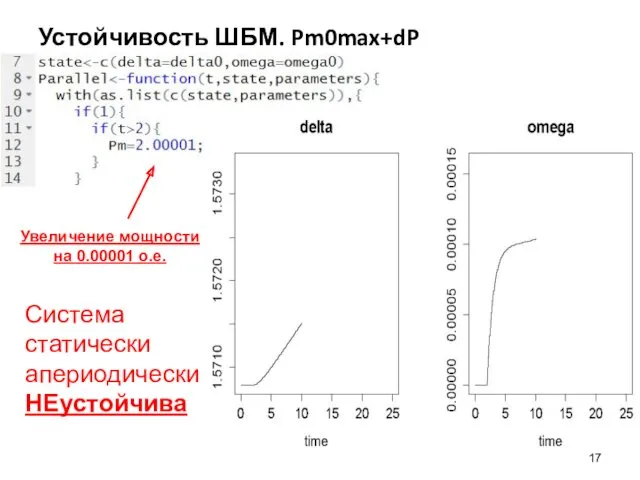
- 17. Устойчивость ШБМ. Pm0max+dP Увеличение мощности на 0.00001 о.е. Система статически апериодически НЕустойчива
- 18. Работа в статически неустойчивой точке δ0=0.93рад=53град. – статически устойчивая точка, которой соответствует Pm0=1.6о.е. δ0= π -
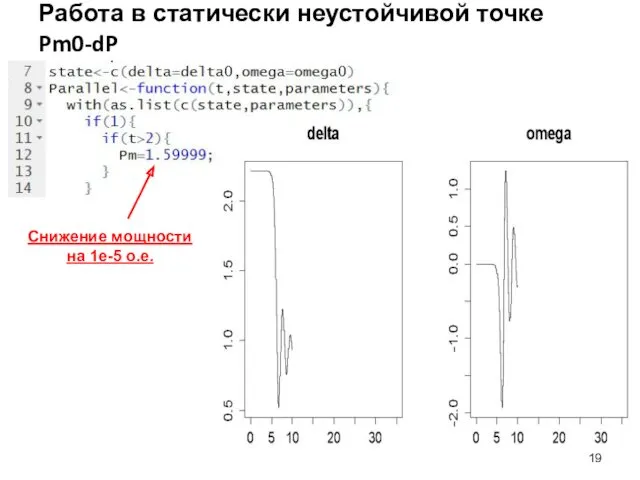
- 19. Работа в статически неустойчивой точке Pm0-dP Снижение мощности на 1e-5 о.е.
- 21. Скачать презентацию













 Презентация Дружба в виртуальном пространстве
Презентация Дружба в виртуальном пространстве Ультразвуковой дальномер и СОМ порт
Ультразвуковой дальномер и СОМ порт Проблемы применения новых оральных антикоагулянтов в клинической практике
Проблемы применения новых оральных антикоагулянтов в клинической практике Мои гости
Мои гости География всемирных экономических отношений
География всемирных экономических отношений ВПР 5 кл
ВПР 5 кл ОДЕЖДА ХАНТОВ И МАНСИ
ОДЕЖДА ХАНТОВ И МАНСИ Оболочки головного мозга
Оболочки головного мозга Разработка услуги по устранению дефектов кузова без повреждения лакокрасочного покрытия
Разработка услуги по устранению дефектов кузова без повреждения лакокрасочного покрытия Путешествие к истокам. Фотохроника. Волгоград, храм Николая Чудотворца на Тулака
Путешествие к истокам. Фотохроника. Волгоград, храм Николая Чудотворца на Тулака Фармакоэпидемиология и фармакоэкономика. Использование экономической оценки, как элемент принятия решений в медицине
Фармакоэпидемиология и фармакоэкономика. Использование экономической оценки, как элемент принятия решений в медицине Половинки (первый и последний звук)
Половинки (первый и последний звук) Рабочее место кассира Фрисби
Рабочее место кассира Фрисби Образец. 7 класс
Образец. 7 класс Unusual and extraordinary celebrations and festivals around the world
Unusual and extraordinary celebrations and festivals around the world Системы коммутации. Элементы сети ТфОП. (Лекция 3)
Системы коммутации. Элементы сети ТфОП. (Лекция 3) Безопасность детей в быту
Безопасность детей в быту ВИЧ-инфекция
ВИЧ-инфекция Методика проведения специсследований съемных носителей USB 3.0
Методика проведения специсследований съемных носителей USB 3.0 Атмосферное давление
Атмосферное давление  История развития интернета. Способы и скоростные характеристики подключения. Интернеттехнологии. Лекция 35-36
История развития интернета. Способы и скоростные характеристики подключения. Интернеттехнологии. Лекция 35-36 Платежный баланс Статистическая система мирохозяйственных связей
Платежный баланс Статистическая система мирохозяйственных связей Собрание
Собрание Плоскость, касательная к поверхности, нормаль поверхности
Плоскость, касательная к поверхности, нормаль поверхности Устройство шлюпки ЯЛ-6
Устройство шлюпки ЯЛ-6 Обмен углеводов
Обмен углеводов Резкость изображения
Резкость изображения Бег на средние дистанции
Бег на средние дистанции