Содержание
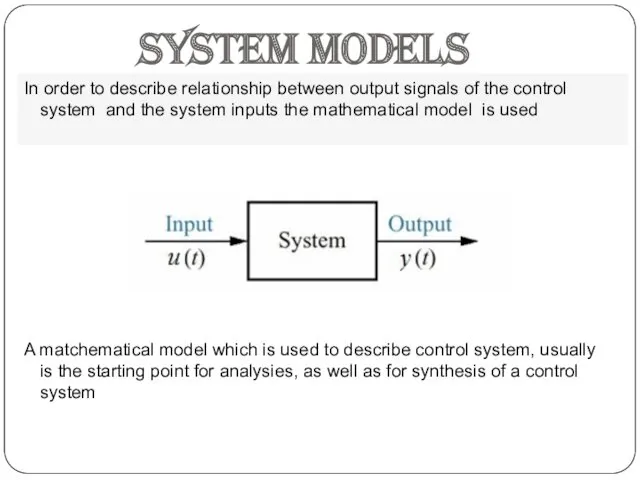
- 2. System models In order to describe relationship between output signals of the control system and the
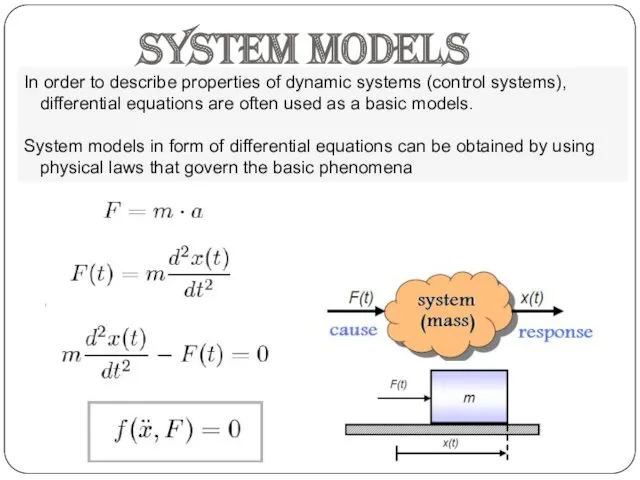
- 3. System models In order to describe properties of dynamic systems (control systems), differential equations are often
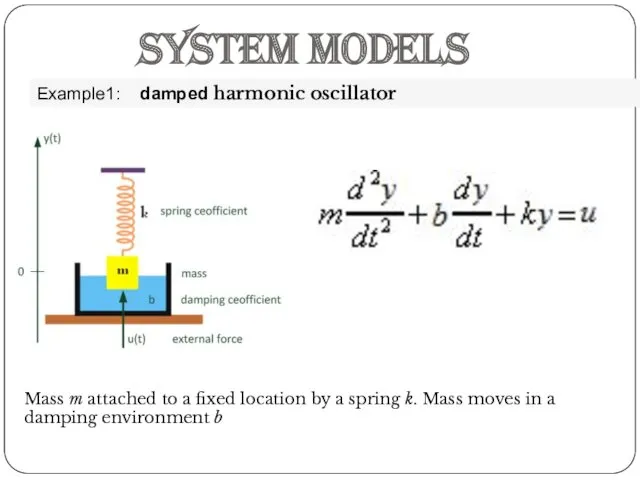
- 4. System models Example1: damped harmonic oscillator Mass m attached to a fixed location by a spring
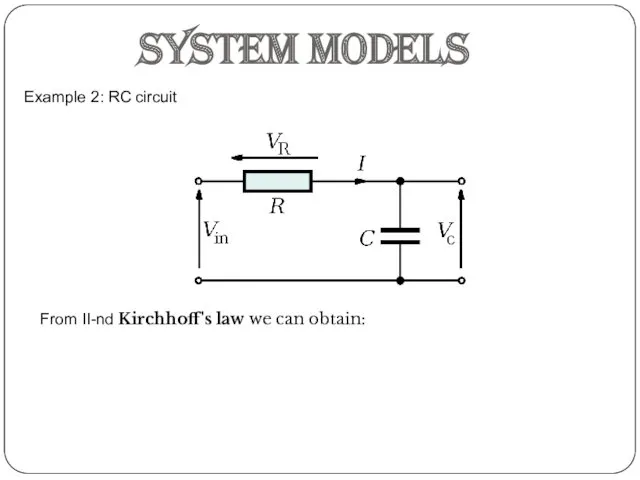
- 5. Example 2: RC circuit System models From II-nd Kirchhoff's law we can obtain:
- 6. System models Classification of dynamical system models: I. 1. Linear my” + by’ + ky =
- 7. State space models The state space model is an anather way (kind of an ordered way)
- 8. x(t) - state variables, are the smallest possible subset of system variables that can represent the
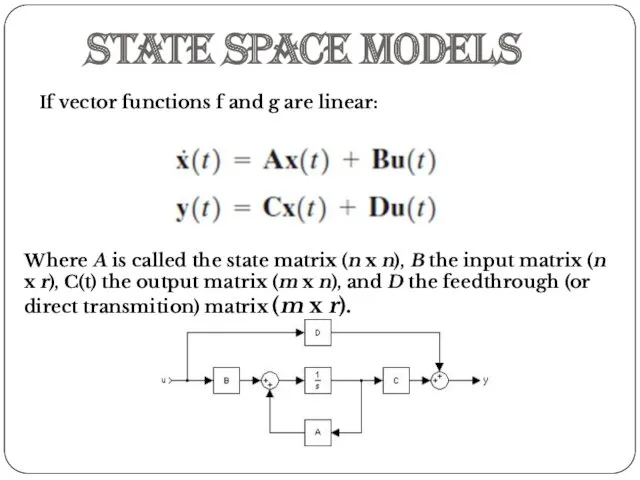
- 9. State space models If vector functions f and g are linear: Where A is called the
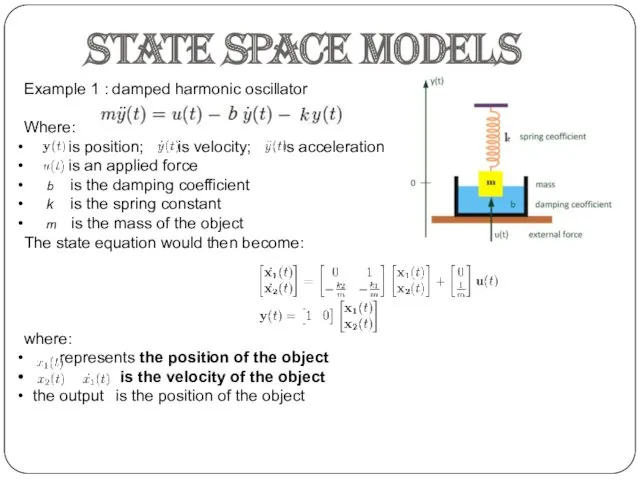
- 10. Example 1 : damped harmonic oscillator Where: is position; is velocity; is acceleration is an applied
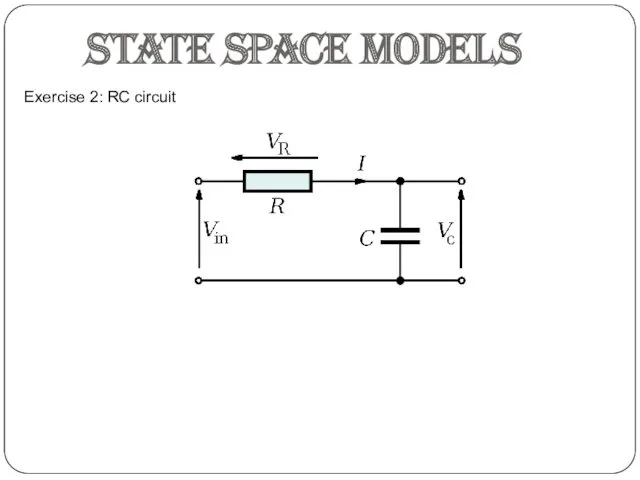
- 11. Exercise 2: RC circuit State space models
- 12. The Laplace transform is a linear operation of a function f(t) with a real argument t
- 13. Example 1: Heaviside step function or unit step function Laplace Transform f(t) = 1(t) Exercise 2:
- 14. Laplace Transform It is often convenient to use the differentiation property of the Laplace transform to
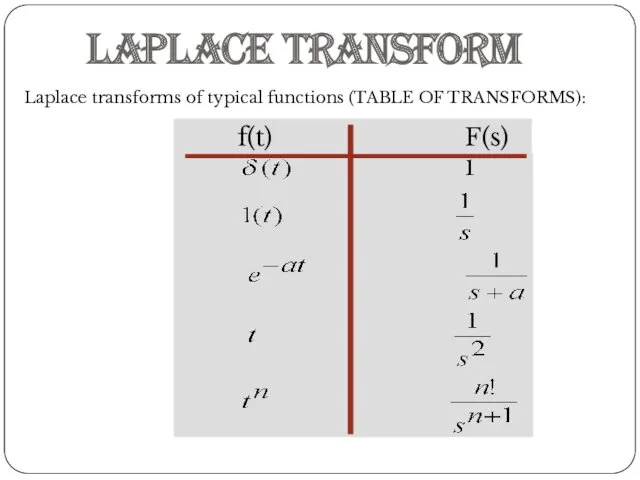
- 15. f(t) F(s) Laplace Transform Laplace transforms of typical functions (TABLE OF TRANSFORMS):
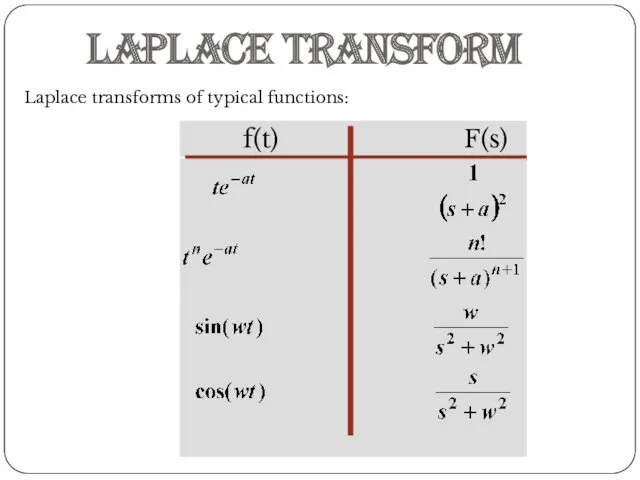
- 16. Laplace Transform Laplace transforms of typical functions: f(t) F(s)
- 17. Laplace Transform Laplace transform properties: 1.
- 18. Laplace Transform Laplace transform properties: 2. becomes
- 19. Laplace Transform Laplace transform properties: 3. 4.
- 20. Laplace Transform Laplace transform properties: 5. 6. The final value theorem is useful because it gives
- 21. Inverse Laplace Transform The Inverse Laplace Transform is defined by: If the algebraic equation is solved
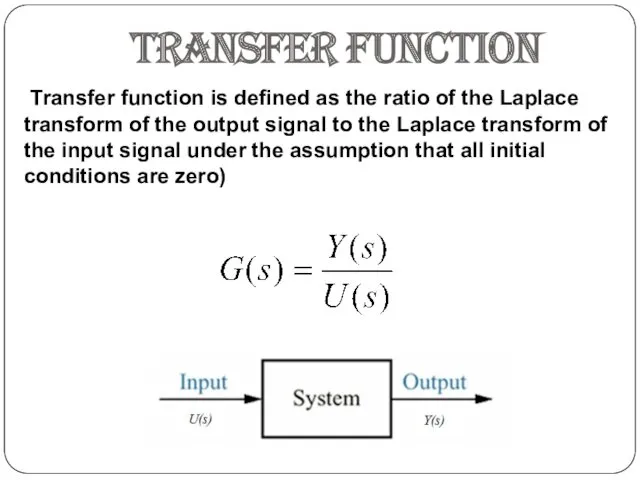
- 22. TRANSFER FUNCTION Transfer function is defined as the ratio of the Laplace transform of the output
- 23. TRANSFER FUNCTION From general differential equetion: we can obtain transfer function :
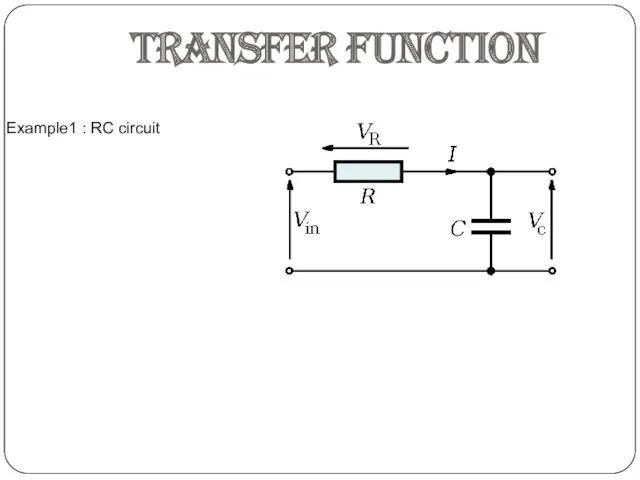
- 24. Example1 : RC circuit TRANSFER FUNCTION
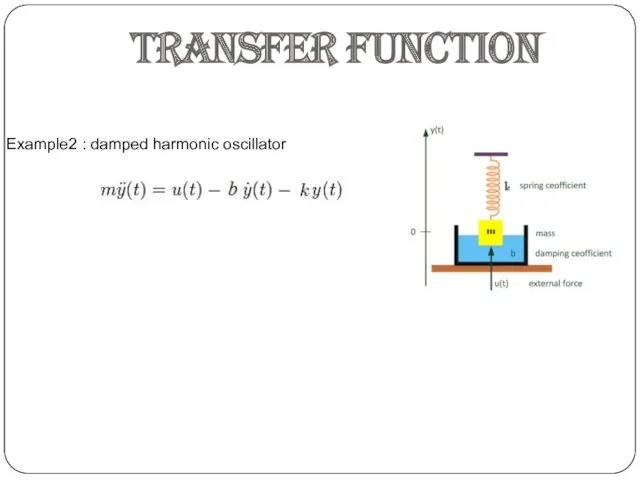
- 25. Example2 : damped harmonic oscillator TRANSFER FUNCTION
- 26. If we obtain the roots in the numerator and denominator of transfer function: we can change
- 27. We can transform State space model to transfer function by performing following operations: Since the transfer
- 28. Control systems often works with small changes of input and output quantities around some given steady
- 29. Static linearization example: Model linearization Static linearization exercise: Pendulum T=m*g*l*sin(x) (To,xo) = (0,0)
- 30. Linearization of differential equation (dynamic linearization) Model linearization Taylor series expansion in steady state point :
- 31. Linearization of differential equation (dynamic linearization) example: DC generator equation: Model linearization
- 32. THANK YOU
- 34. Скачать презентацию



















 Открытка к Дню защитника Отечества
Открытка к Дню защитника Отечества Свойства параллельных плоскостей
Свойства параллельных плоскостей Танцы народов Кавказа
Танцы народов Кавказа Разложение многочленов на множители
Разложение многочленов на множители презентация Фронтовая тетрадь- песенник Трифонова С.И.
презентация Фронтовая тетрадь- песенник Трифонова С.И. Развитие чувства времени у детей старшего дошкольного возраста
Развитие чувства времени у детей старшего дошкольного возраста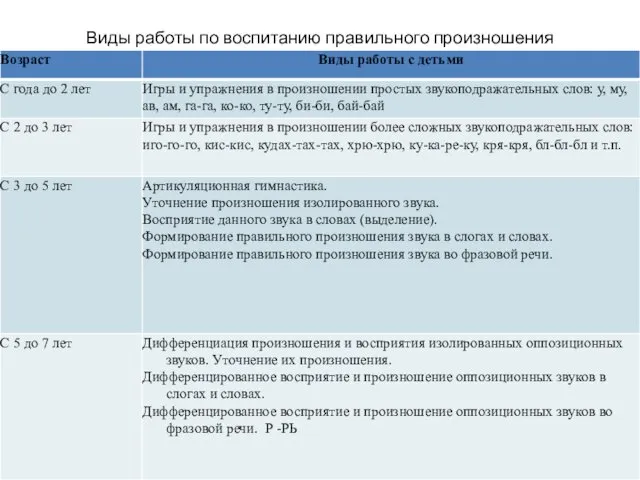 Виды работы по воспитанию правильного произношения
Виды работы по воспитанию правильного произношения Отгадай слово по первым звукам
Отгадай слово по первым звукам Реформы в 1900 – 1912 гг
Реформы в 1900 – 1912 гг Электрические трансформаторы. Расчет трансформаторов
Электрические трансформаторы. Расчет трансформаторов класс Вред
класс Вред Морфологический разбор имени существительного
Морфологический разбор имени существительного Инструктаж по ТБ и ОТ. Введение: инструктаж, знакомство
Инструктаж по ТБ и ОТ. Введение: инструктаж, знакомство Прсоединение Крыма к России
Прсоединение Крыма к России Каменный век на Кавказе
Каменный век на Кавказе Контроль за точністю руху сільськогосподарської техніки та обладнання
Контроль за точністю руху сільськогосподарської техніки та обладнання К. Паустовский Теплый хлеб
К. Паустовский Теплый хлеб Анализ работы фонда скважин Сологаевского месторождения пласта Д
Анализ работы фонда скважин Сологаевского месторождения пласта Д Мастер-класс Использование технологии развития критического мышления через чтение и письмо на примере урока чтения во 2 классе по теме В. Драгунский Заколдованная буква
Мастер-класс Использование технологии развития критического мышления через чтение и письмо на примере урока чтения во 2 классе по теме В. Драгунский Заколдованная буква Microsoft Word. Создание первого документа Word
Microsoft Word. Создание первого документа Word практические работы
практические работы Цели компании Coca-Cola
Цели компании Coca-Cola Презентация Дифференциация звуков Б-П
Презентация Дифференциация звуков Б-П مهارات الحاسب الآلي
مهارات الحاسب الآلي Презентация Петр Великий
Презентация Петр Великий Авраам Линкольн
Авраам Линкольн Регулирование частоты вращения приводов судовых устройств. Техническое обслуживание Дизель-генераторов. (Билет 30)
Регулирование частоты вращения приводов судовых устройств. Техническое обслуживание Дизель-генераторов. (Билет 30) Путешествие в космос
Путешествие в космос