Содержание
- 2. 2. Системы счисления 2.1. Основы систем счисления. 2.2. Двоичная, восьмеричная, шестнадцатеричная и десятичная системы счисления. 2.3.
- 3. 2.1. Основы систем счисления. 2.1.1. Определения Система счисления — это совокупность приемов и правил, по которым
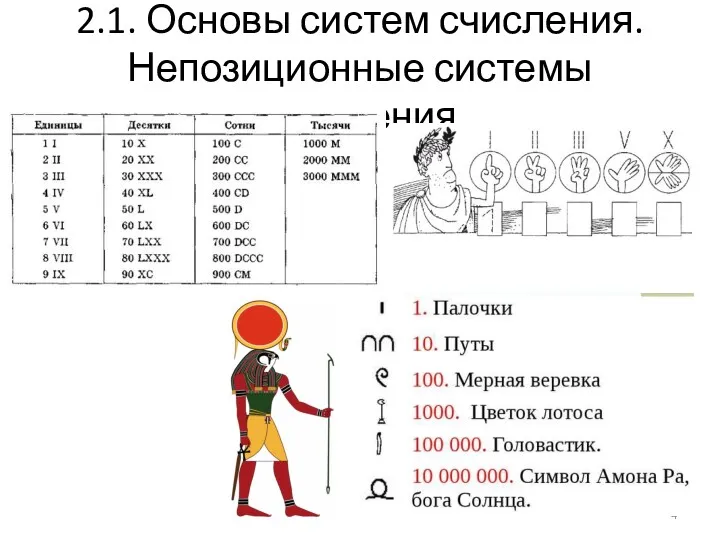
- 4. 2.1. Основы систем счисления. Непозиционные системы счисления
- 5. 2.1. Основы систем счисления. Славянская система счисления
- 6. 2.1. Основы систем счисления. Как появились цифры?
- 7. Как появились цифры? Арабские цифры возникли в Индии не позднее V века. Тогда же было открыто
- 8. Как появились цифры? Названия цифр на санскрите (Сев. Индия)
- 9. 2.1. Основы систем счисления. 2.1.2. Позиционные системы счисления Основание позиционной системы счисления — количество различных цифр,
- 10. 2.1. Основы систем счисления. 2.1.2. Позиционные системы счисления В каждой системе счисления цифры упорядочены в соответствии
- 11. 2.1. Основы систем счисления. 2.1.2. Позиционные системы счисления Продвижение цифры
- 12. 2.2. Двоичная, восьмеричная, шестнадцатеричная и десятичная системы счисления. Кроме десятичной в вычислительной технике широко используются системы
- 13. 2.2. Двоичная, восьмеричная, шестнадцатеричная и десятичная системы счисления. Причины применения двоичной системы в вычислительной технике: для
- 14. 2.2. Двоичная, восьмеричная, шестнадцатеричная и десятичная системы счисления Причины применения восьмеричной и шестнадцатеричной систем: читаются почти
- 15. 2.2. Двоичная, восьмеричная, шестнадцатеричная и десятичная системы счисления Чтобы перевести число из двоичной системы в восьмеричную
- 16. 2.3. Понятие об алгоритме преобразования информации из двоичной в десятичную системы счисления и обратно. 2.3.1. Как
- 17. 2.3.2. Как перевести правильную десятичную дробь в любую другую позиционную систему счисления? Для перевода правильной десятичной
- 18. 2.3.2. Как перевести правильную десятичную дробь в любую другую позиционную систему счисления? Пример. Переведем число 0,36
- 19. 2.3.3. Как перевести число из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную? Перевод в десятичную систему числа
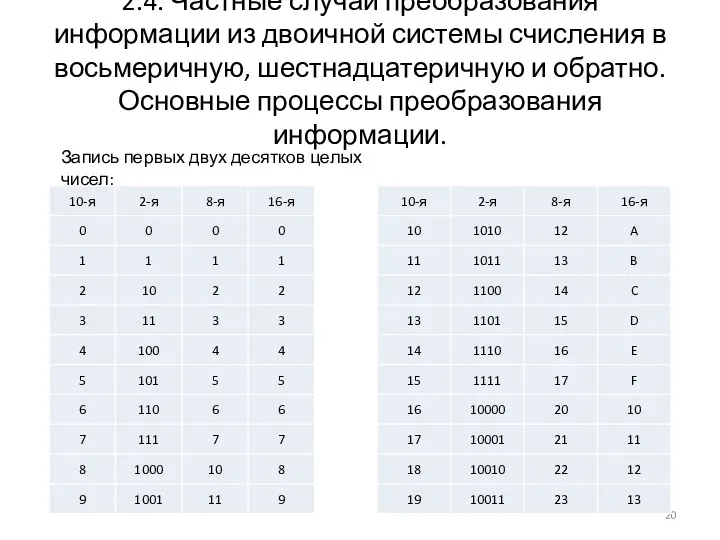
- 20. 2.4. Частные случаи преобразования информации из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно. Основные процессы
- 21. 2.4.1. Арифметические операции в позиционных системах счисления Основные арифметические операции: сложение, вычитание, умножение, деление. Правила выполнения
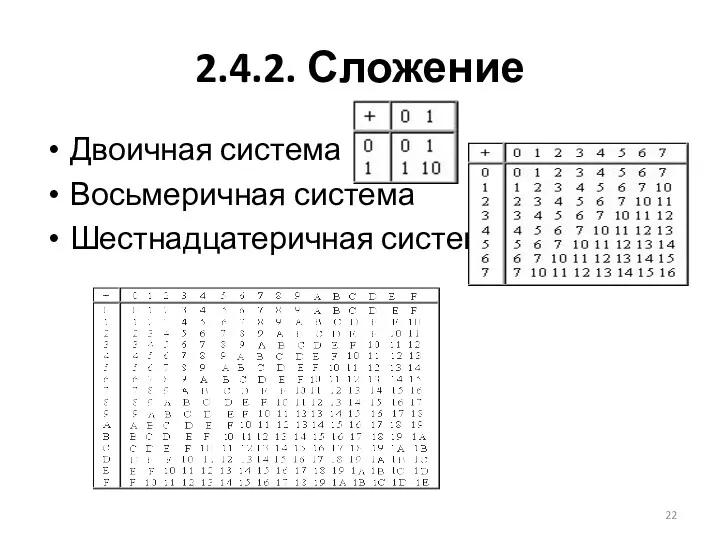
- 22. 2.4.2. Сложение Двоичная система Восьмеричная система Шестнадцатеричная система
- 23. 2.4.2. Сложение. Пример Сложим числа 15 и 6. Шестнадцатеричная: F16+616 Ответ: 15+6=2110=101012=258=1516 Проверка. Преобразуем полученные суммы
- 24. 2.4.2. Сложение. Пример F+1=1016 FF+1=10016 7+1=108 17+1=208
- 25. 2.4.3. Вычитание Вычтем число 59,75 из числа 201,25. Ответ: 201,2510-59,7510=141,510=10001101,12=215,48=8D,816 Проверка. Преобразуем полученные разности к десятичному
- 26. 2.4.3. Вычитание 10-1=F или 9 или 7 или 1 или ? 100-1=FF или 99 или 77
- 27. 2.4.4. Умножение Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения
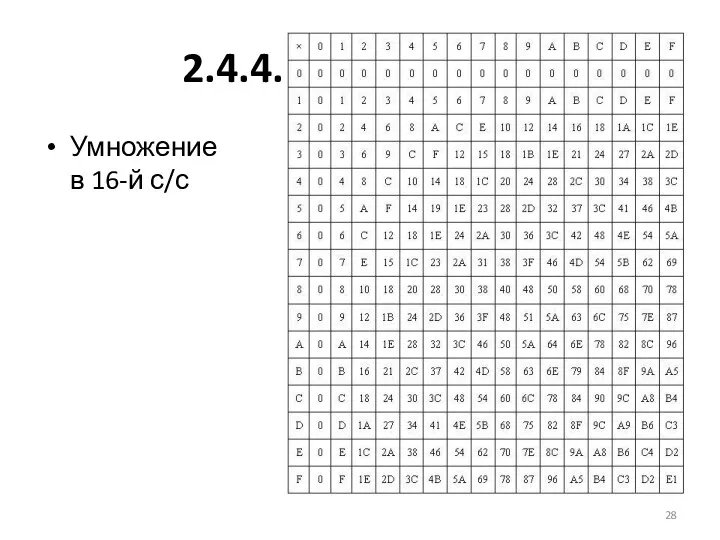
- 28. 2.4.4. Умножение Умножение в 16-й с/с
- 29. 2.4.4. Умножение. Пример Перемножим числа 115 и 51. Ответ: 115.51=586510=10110111010012=133518. Проверка. Преобразуем полученные произведения к десятичному
- 30. 2.4.5. Деление Деление в любой позиционной системе счисления производится по тем же правилам, как и деление
- 31. 2.4.5. Деление. Пример Разделим число 35 на число 14. Восьмеричная: 438:168 Ответ: 35:14=2,510=10,12=2,48 Проверка. Преобразуем полученные
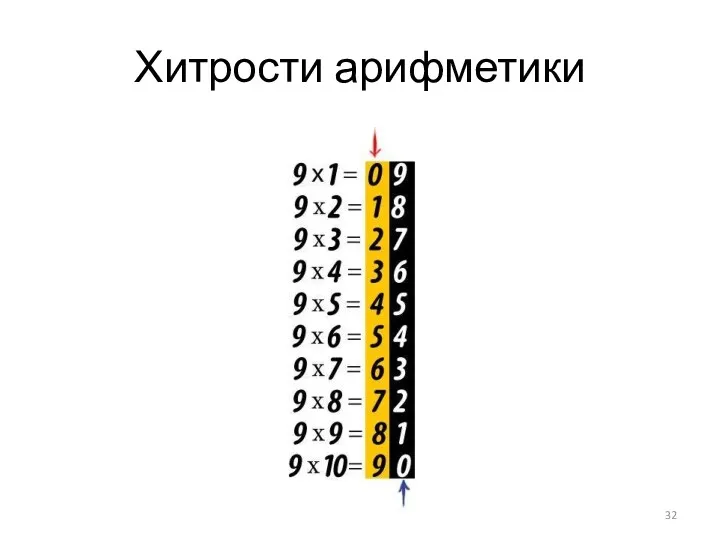
- 32. Хитрости арифметики
- 33. Хитрости арифметики
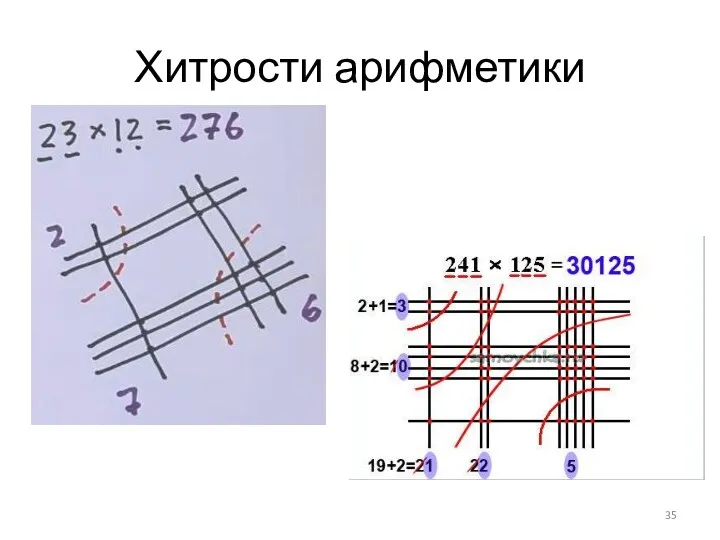
- 34. Хитрости арифметики
- 35. Хитрости арифметики
- 36. Русская деревенская школа конца XIX века во время урока арифметики Сергея Александровича Рачинского
- 38. Скачать презентацию




























 Мастер класс Африканские бусы из бумаги
Мастер класс Африканские бусы из бумаги Технология производства продуктов овцеводства
Технология производства продуктов овцеводства Птицы (фотографии)
Птицы (фотографии) 1-е и 2-е Послания к Фессалоникийцам (Солунянам) апостола Павла
1-е и 2-е Послания к Фессалоникийцам (Солунянам) апостола Павла Экономические реформы в период перестройки 1985-1991 гг
Экономические реформы в период перестройки 1985-1991 гг Описать технологию ремонта скрытой электропроводки
Описать технологию ремонта скрытой электропроводки Острый живот при воспалительных заболеваниях органов малого таза
Острый живот при воспалительных заболеваниях органов малого таза Компьютербасты адамдар
Компьютербасты адамдар Н.И.Роговцева. Технология. 3 класс. Проект Детская площадка
Н.И.Роговцева. Технология. 3 класс. Проект Детская площадка Введение в систематику. Низшие растения
Введение в систематику. Низшие растения Кардиоэмболический инсульт
Кардиоэмболический инсульт sec101-lec04-pub
sec101-lec04-pub Образовательные технологии, используемые на уроках химии для повышения мотивации обучения
Образовательные технологии, используемые на уроках химии для повышения мотивации обучения Национальная и конфессиональная политика в Республике Калмыкия
Национальная и конфессиональная политика в Республике Калмыкия Печатная реклама. Приюты для животных
Печатная реклама. Приюты для животных Кормление телят на ферме
Кормление телят на ферме Химия и фотография
Химия и фотография Наркотики, и это еще не вся правда о них
Наркотики, и это еще не вся правда о них Логические выражения и логические операции
Логические выражения и логические операции Урок-презентация Строим школьный дом
Урок-презентация Строим школьный дом Палач человечества - алкоголь
Палач человечества - алкоголь Легкая атлетика
Легкая атлетика Люблю тебя, мой край родной, Воскресенск!
Люблю тебя, мой край родной, Воскресенск! Лев Николаевич Толстой
Лев Николаевич Толстой оформление реферата
оформление реферата Работа с инструментом Перо
Работа с инструментом Перо Презентация Электролиз
Презентация Электролиз Клиническая физиология кислотно-щелочного равновесия
Клиническая физиология кислотно-щелочного равновесия