Содержание
- 2. Понятие временной и емкостной сложности алгоритмов Время работы алгоритма и используемую алгоритмом память можно рассматривать как
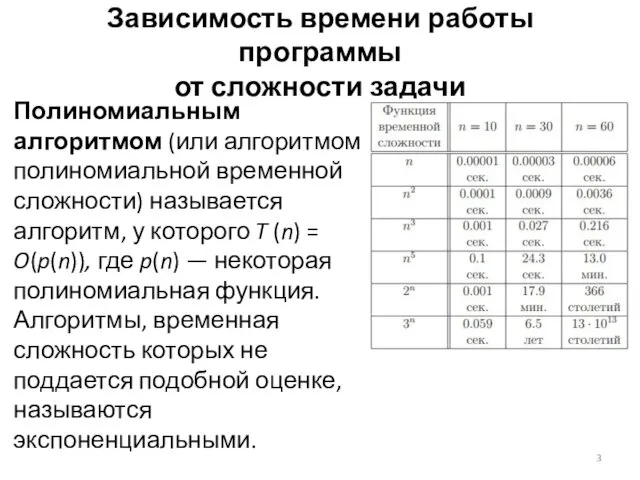
- 3. Зависимость времени работы программы от сложности задачи Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм,
- 4. Разные алгоритмы имеют различную временную сложность T(n) и влияние того, какие алгоритмы достаточно эффективны, а какие
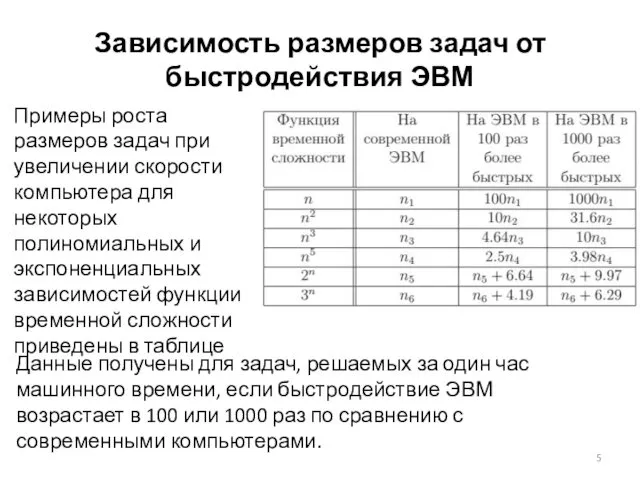
- 5. Зависимость размеров задач от быстродействия ЭВМ Данные получены для задач, решаемых за один час машинного времени,
- 6. Сколько вычислений должна потребовать задача, чтобы мы сочли ее труднорешаемой? Общепринято, что если задачу нельзя решить
- 7. Практическая оценка временной сложности
- 8. Практическая оценка временной сложности
- 9. Практическая оценка временной сложности
- 10. Анализ временной сложности рекурсивных алгоритмов
- 11. P-задачи и NP–задачи
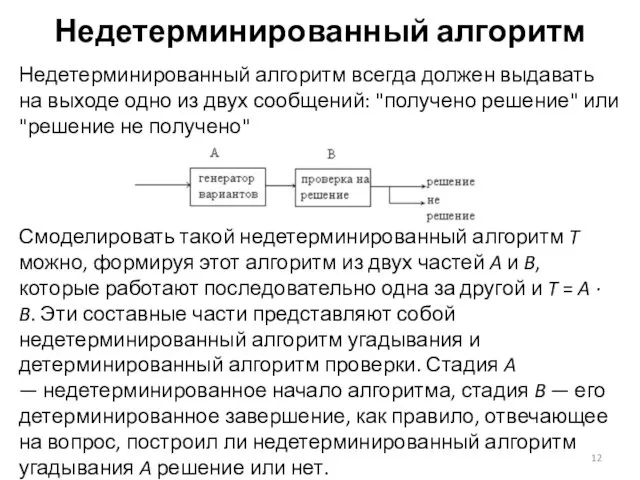
- 12. Недетерминированный алгоритм Недетерминированный алгоритм всегда должен выдавать на выходе одно из двух сообщений: "получено решение" или
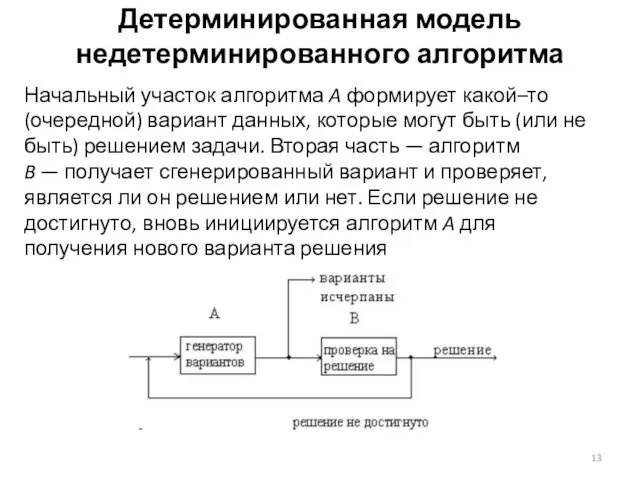
- 13. Детерминированная модель недетерминированного алгоритма Начальный участок алгоритма A формирует какой–то (очередной) вариант данных, которые могут быть
- 14. Всякая задача, разрешимая за полиномиальное время детерминированным алгоритмом, разрешима также за полиномиальное время недетерминированным алгоритмом, т.е.
- 18. Вопрос о равенстве классов сложности P и NP Проблема равенства классов P и NP является одной
- 19. Что если P=NP? Целый ряд задач, связанных с поиском в экспоненциальном пространстве, получит эффективное полиномиальное решение.
- 20. NP –полные задачи В классе NP содержатся NP –полные задачи. Это NP –задачи, для решения которых
- 21. Примеры NP –полных задач
- 22. Примеры NP –полных задач
- 23. Методы решения NP-полных задач В соответствии с представлением алгоритма решения NP–полных задач с помощью алгоритма угадывания
- 25. Скачать презентацию











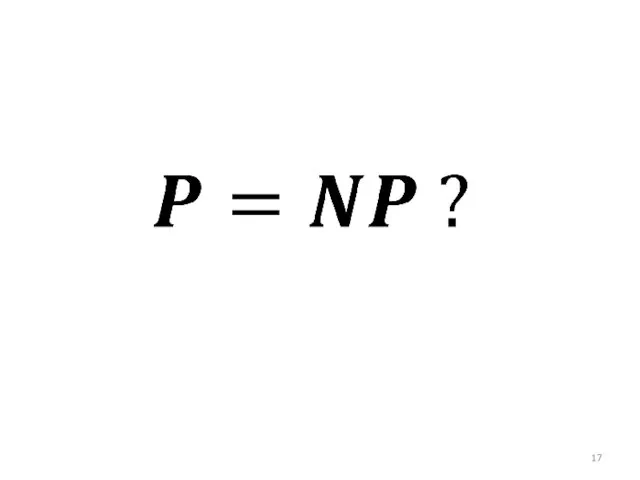






 органическая химия 10 класс общеобразовательная группа Аминокислоты
органическая химия 10 класс общеобразовательная группа Аминокислоты Управление конфликтами
Управление конфликтами Мастер обработки цифровой информации
Мастер обработки цифровой информации Взаимодействие ДОУ и семьи
Взаимодействие ДОУ и семьи Политическая культура и социализация
Политическая культура и социализация Собрание для будущих первоклассников
Собрание для будущих первоклассников Отчет по неделе игры и игрушки (старшая группа)
Отчет по неделе игры и игрушки (старшая группа) Международное гуманитарное право
Международное гуманитарное право Ой қозғау. 8 класс
Ой қозғау. 8 класс RamblerCo template
RamblerCo template Роман Война и мир. История создания, проблематика, жанр и композиция
Роман Война и мир. История создания, проблематика, жанр и композиция Артериялық гипертензия
Артериялық гипертензия разработки к урокам по темам Вселенная и Человек на Земле
разработки к урокам по темам Вселенная и Человек на Земле Архитектура 2-й половины XIХ в. Рационализм
Архитектура 2-й половины XIХ в. Рационализм Духовная жизнь
Духовная жизнь The rules of letter writing
The rules of letter writing Конспект занятия по обучению грамоте в подготовительной логопедической группе с обучающимися ОНР по теме Буква О.
Конспект занятия по обучению грамоте в подготовительной логопедической группе с обучающимися ОНР по теме Буква О. Міжнародні норми охорони праці в галузі
Міжнародні норми охорони праці в галузі Хрящевые рыбы
Хрящевые рыбы Одежда
Одежда Усиление каменных конструкций
Усиление каменных конструкций Начало Реформации в Европе
Начало Реформации в Европе Помощь при подготовке к экзаменам
Помощь при подготовке к экзаменам Детский центр развития Василёк
Детский центр развития Василёк Предметно-практическая деятельность как средство развития связной речи у младших школьников, имеющих нарушения слуха.
Предметно-практическая деятельность как средство развития связной речи у младших школьников, имеющих нарушения слуха. Автотрансформаторы
Автотрансформаторы История слова кролик
История слова кролик Элективный курс Моя будущая профессия- технолог
Элективный курс Моя будущая профессия- технолог