Содержание
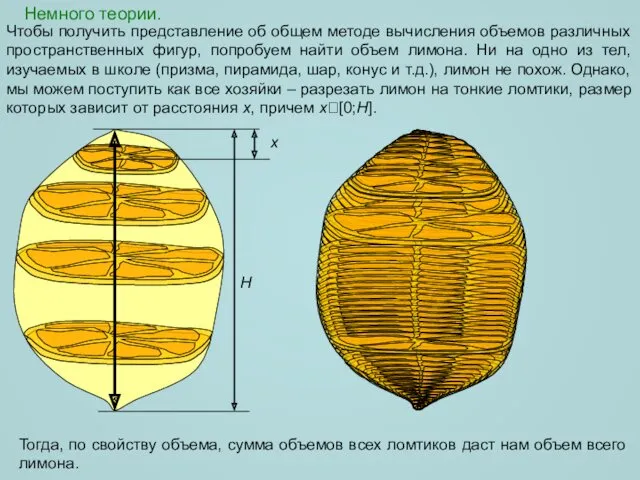
- 2. Немного теории. Чтобы получить представление об общем методе вычисления объемов различных пространственных фигур, попробуем найти объем
- 3. Немного теории. H x x С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными
- 4. Немного теории (базовые классы могут пропустить). H x x Если принять число разбиений бесконечно большим числом
- 5. I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x H x[0;H] 0 Площадь
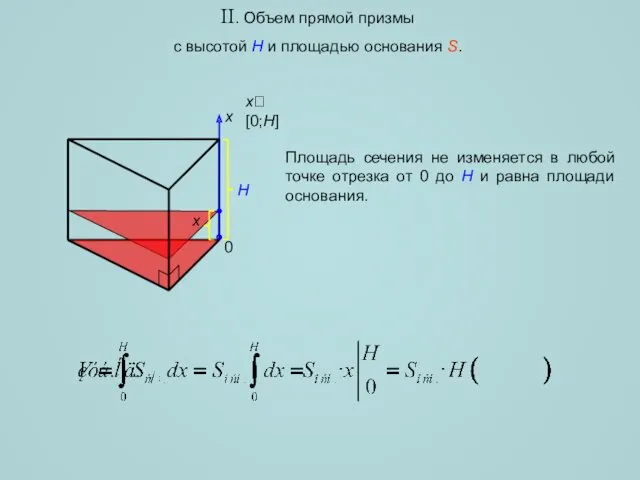
- 6. II. Объем прямой призмы с высотой H и площадью основания S. x x[0;H] H 0 Площадь
- 7. III. Объем n-угольной прямой призмы с высотой H и площадью основания S. x x[0;H] H 0
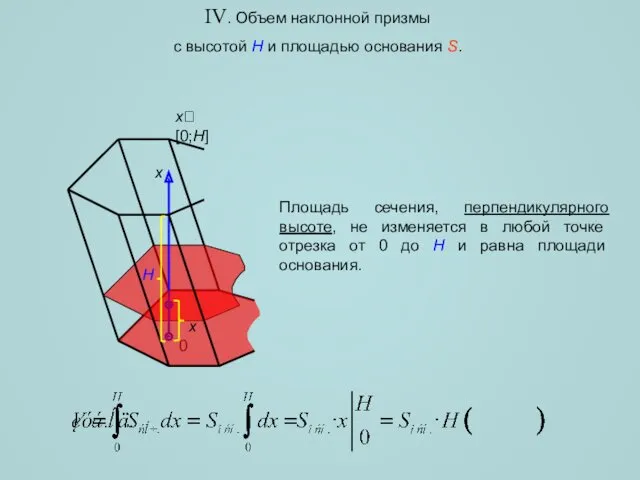
- 8. IV. Объем наклонной призмы с высотой H и площадью основания S. Площадь сечения, перпендикулярного высоте, не
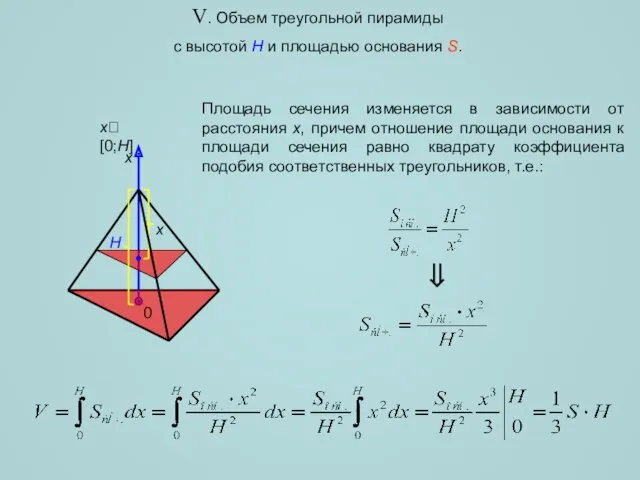
- 9. V. Объем треугольной пирамиды с высотой H и площадью основания S. H x x[0;H] ⇒ x
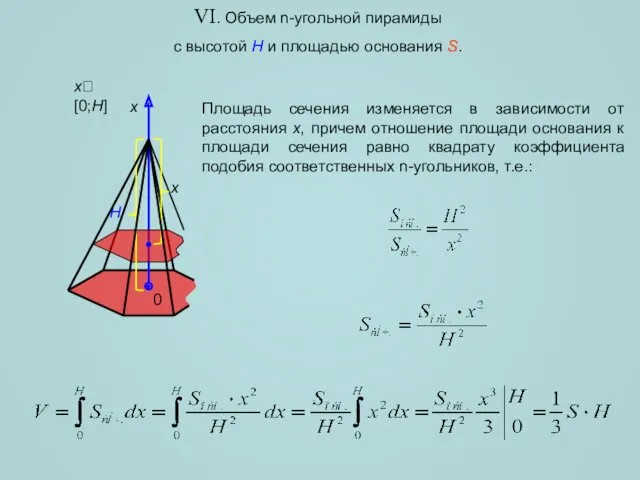
- 10. VI. Объем n-угольной пирамиды с высотой H и площадью основания S. H x Площадь сечения изменяется
- 11. VII. Объем усеченной пирамиды. текст
- 12. VIII. Объем цилиндра с высотой H и площадью основания S. x x[0;H] H 0 x Площадь
- 13. IX. Объем конуса с высотой H и площадью основания S. x x[0;H] H x Площадь сечения
- 14. X. Объем усеченного конуса. текст
- 15. XI. Объем шара с радиусом R. Найдем объем полушария, как бесконечную интегральную сумму площадей сечения с
- 16. XII. Объем шарового сегмента. Вывод объема шарового сегмента с высотой h и радиусом основания r отличается
- 17. XIII. Объем шарового слоя. текст
- 19. Скачать презентацию









 Выбор и подготовка материалов для резки
Выбор и подготовка материалов для резки Изготовление цветка гвоздики
Изготовление цветка гвоздики Зороастризм
Зороастризм Дошкольное детство. Психология развития и возрастная психология
Дошкольное детство. Психология развития и возрастная психология Types of transport
Types of transport Стихи на уроках - 8
Стихи на уроках - 8 Механические методы индукции родов
Механические методы индукции родов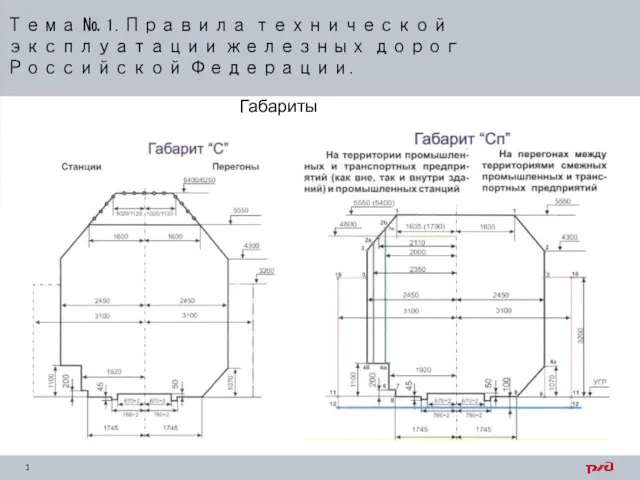 Правила технической эксплуатации железных дорог Российской Федерации
Правила технической эксплуатации железных дорог Российской Федерации Распорный анкерный болт
Распорный анкерный болт Компьютерные технологий в обучении математике
Компьютерные технологий в обучении математике Международный день родного языка - 21 февраля. Викторина Я знаю удмуртский язык
Международный день родного языка - 21 февраля. Викторина Я знаю удмуртский язык Исследование и разработка системы автоматического управления процессом сушки аммиачной селитры
Исследование и разработка системы автоматического управления процессом сушки аммиачной селитры Гештальт-терапия как практико-ориентированный подход в психологии
Гештальт-терапия как практико-ориентированный подход в психологии Прекрасное Далеко. Слова Ю. Энтина. Музыка Е. Крылатова
Прекрасное Далеко. Слова Ю. Энтина. Музыка Е. Крылатова История возникновения образа Золотой век Голливуда 40-х годов
История возникновения образа Золотой век Голливуда 40-х годов В Новый год по странам мира
В Новый год по странам мира Winemaking In Russia
Winemaking In Russia Создание контента в Instagram
Создание контента в Instagram История происхождения и развития шрифтов
История происхождения и развития шрифтов Трудный диалог с учёбой, или как помочь своему ребёнку учиться
Трудный диалог с учёбой, или как помочь своему ребёнку учиться Симптомы поражения различных долей головного мозга, мозжечка, экстрапирамидных структур
Симптомы поражения различных долей головного мозга, мозжечка, экстрапирамидных структур Регистры
Регистры Зимние Олимпийские игры XX - XXII
Зимние Олимпийские игры XX - XXII ЛДО Прикамье отряд: Еще не взрослые! 5-7 классы
ЛДО Прикамье отряд: Еще не взрослые! 5-7 классы Бытие. Развитие. Детерминизм. Тема №5
Бытие. Развитие. Детерминизм. Тема №5 Река и ее части
Река и ее части Кордиц совет (1)
Кордиц совет (1) Клиническая физиология кислотно-щелочного равновесия
Клиническая физиология кислотно-щелочного равновесия