Содержание
- 2. Zależności funkcyjne Zależności funkcyjne między atrybutami są rodzajem warunków integralności. Definicja 3. Niech będzie dany zbiór
- 3. Zależności funkcyjne Dla zależności funkcyjnych sformułowano zbiór reguł wnioskowania, które pozwalają na wyprowadzenie nowych zależności na
- 4. AKSJOMATY ARMSTRONGA A1. Y ⊆ X ⇒ X →Y (zwrotność) A2. X → Y ∧ Z
- 5. AKSJOMATY ARMSTRONGA Dowód A1. t1 (X) = t2 (X) ∧ Y ⊆ X ⇒ t1 (Y)
- 6. AKSJOMATY ARMSTRONGA A2. Dowód przez zaprzeczenie. Załóżmy, że : t1 (XW) = t2 (XW) ∧ t1
- 7. AKSJOMATY ARMSTRONGA A3. ( t1 (X) = t2 (X) ⇒ t1 (Y) = t2 (Y)) ∧
- 8. REGUŁY ARMSTRONGA Z aksjomatów Armstronga wynikają następujące reguły: D1. X → Y ∧ X → Z
- 9. REGUŁY ARMSTRONGA Dowód D1. X → Y ∧ X → Z ⇒ X → YZ X
- 10. REGUŁY ARMSTRONGA Dowód D2. X → Y ∧ WY → Z ⇒ XW → Z X
- 11. REGUŁY ARMSTRONGA Dowód D3. X → Y ∧ Z ⊆ Y ⇒ X → Z Z
- 12. REGUŁY ARMSTRONGA Zbiór reguł wnioskowania jest zupełny (sound) i kompletny (complete). Oznacza to, że wszystkie wyprowadzone
- 13. Konsekwencja logiczna Oznaczmy przez F zbiór zależności funkcyjnych między atrybutami schematu SCH. Zależność funkcyjna f jest
- 14. Domknięcie zbioru zależności funkcyjnych F+ Jest to zbiór zależności funkcyjnych będących konsekwencjami logicznymi F
- 15. Nasycenie atrybutu X+ Zbiór F+ zawiera zazwyczaj wiele elementów, nawet jeśli F nie jest zbiorem dużym.
- 16. Nasycenie atrybutu X+ Jest to zbiór atrybutów prostych A takich, że zależność X→A można wyprowadzić zgodnie
- 17. Twierdzenie 1 Zależność X→Y można otrzymać na podstawie reguł wnioskowania ⇔ Y⊆ X+
- 18. Twierdzenie 1 Dowód Załóżmy, że Y = {A1, A2, …, An} 1. Y ⊆ X+. Zgodnie
- 19. 2. X → Y X → Y ⇒ X → Ai. (D3) Oznacza to, że Ai
- 20. 1. Przyjmujemy X0 = X 2. W każdym następnym kroku powiększamy Xi , Xi+1 = Xi
- 21. A – zbiór atrybutów B ⊆ A jest reduktem informacyjnym w A wtedy i tylko wtedy
- 22. A – zbiór atrybutów Bl, Br⊆ A, Bl ∩ Br = ∅ Bl jest reduktem asocjacyjnym
- 23. A – zbiór atrybutów Bl, Br⊆ A, Bl ∩ Br = ∅ Redukt asocjacyjny Bl jest
- 24. A – zbiór atrybutów Bl, Br⊆ A, Bl ∩ Br = ∅ Redukt asocjacyjny Bl jest
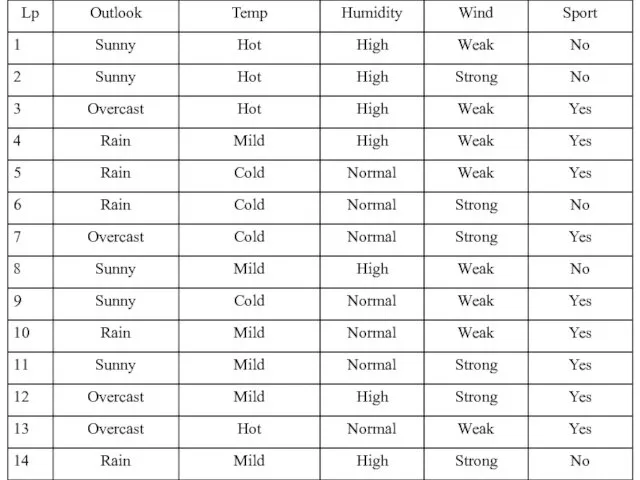
- 26. Jedynym reduktem informacyjnym jest {Outlook, Temp, Humidity, Wind} → {Sport} Redukty asocjacyjne: {Outlook, Temp, Wind} →
- 27. Zbiory zależności F i G są równoważne, jeśli F+ = G+. Mówimy, że F pokrywa G
- 28. Dowód: Niech X → Y ∈ F, Y = {A1, A2 ,…, An}. Niech G będzie
- 29. Wyznaczenie F+ nie jest konieczne. Wystarczy wyznaczyć zbiór minimalny, czyli taki z którego wynikają wszystkie zależności
- 30. Zbiór zależności F jest minimalny jeśli: Prawa strona każdej zależności w F jest pojedyńczym atrybutem Zbiór
- 31. Warunek 2 oznacza, że zbiór F nie zawiera zależności redundantnych. Warunek 3 oznacza, że zbiór F
- 32. Sprawdzanie równoważności zbiorów F i G. G ⊆ F+ F pokrywa G (każdą zależność ze zbioru
- 33. Przy sprawdzaniu równoważności można wykorzystać nasycenie atrybutu 1. Dla każdej zależności X → Y ∈ F
- 34. WYZNACZANIE KLUCZA Twierdzenie 3 Niech R oznacza relację o schemacie SCH. Niech F oznacza zbiór zależności
- 35. WYZNACZANIE KLUCZA Przy wyznaczaniu klucza wykorzystujemy twierdzenie 3. Jako pierwsze przybliżenie przyjmujemy zbiór wszystkich atrybutów: K
- 36. WYZNACZANIE KLUCZA – UWAGI DODATKOWE Przy wyznaczaniu kluczy można wykorzystać następujące własności: 1. Każdy klucz kandydujący
- 37. ROZKŁAD do 3NF Wyznaczyć zbiór minimalny Dla zależności postaci X → Ai utworzyć schemat {X, A1
- 38. ZWIĄZKI WIELOARGUMENTOWE
- 39. Pracownik może brać udział w realizacji różnych projektów. Wymogiem formalnym jest podpisanie kontraktu z odpowiednim wydziałem.
- 40. Pracownik może brać udział w realizacji różnych projektów. Wymogiem formalnym jest podpisanie kontraktu z odpowiednim wydziałem.
- 41. Związki trójargumentowe 4. Każdy projekt jest realizowany na określonym wydziale i wydział może realizować wiele projektów
- 42. Związki trójargumentowe 4. Każdy projekt jest realizowany na określonym wydziale i wydział może realizować wiele projektów
- 43. Związki trójargumentowe 5. Każdy wydział może uczestniczyć w realizacji tylko jednego projektu oraz projekt może być
- 44. Związki trójargumentowe 5. Każdy wydział może uczestniczyć w realizacji tylko jednego projektu oraz projekt może być
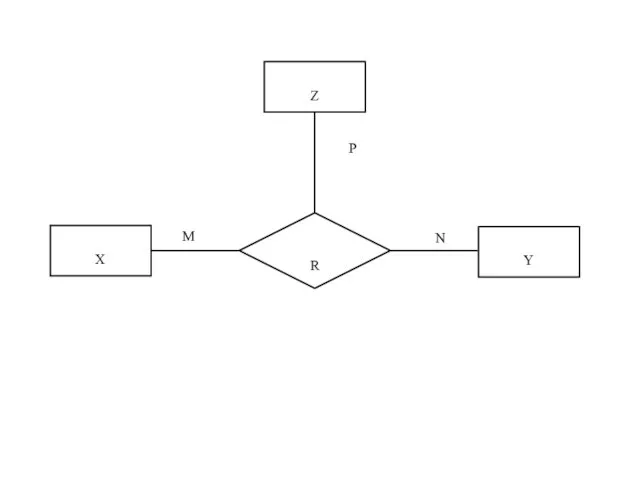
- 45. Związki wieloargumentowe R(X1, X2, … , Xn) n – stopień związku, Xi – klucz i-tego zbioru
- 46. X Y R Z M N P
- 47. Związki wieloargumentowe Związki trójargumentowe 1:1:1, a:1:1, a:b:1, a:b:c Kardynalności związków binarnych nie mogą mniejsze niż kardynalności
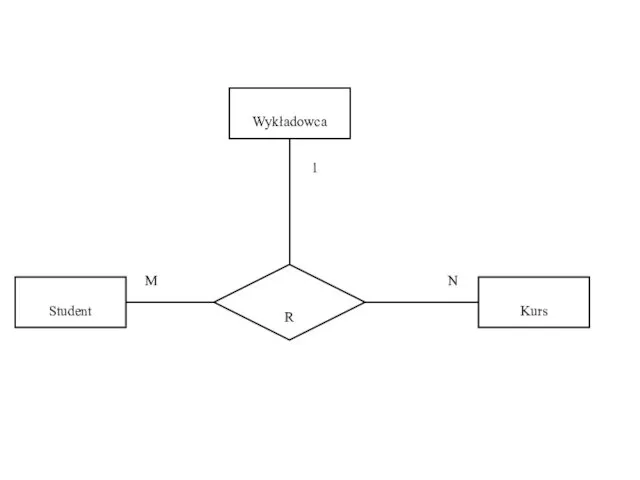
- 48. Student Kurs R Wykładowca M N 1
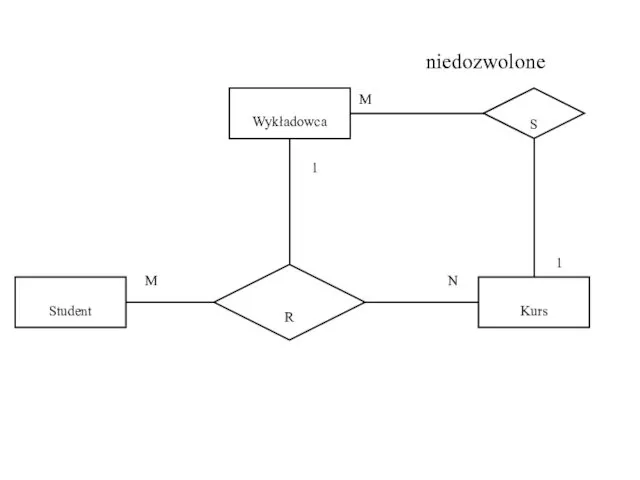
- 49. Student Kurs R Wykładowca M N 1 S M 1 niedozwolone
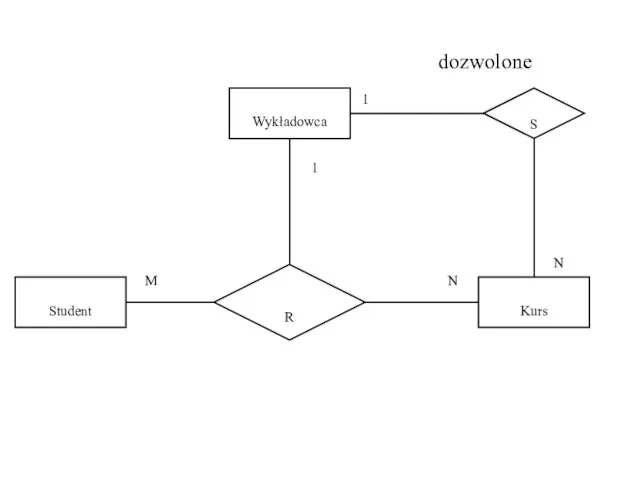
- 50. Student Kurs R Wykładowca M N 1 S 1 N dozwolone
- 51. Związki trójargumentowe XY → Z, XZ → Y, YZ → X 1:1:1 (x1, y1, z1), (x2,
- 52. Związki trójargumentowe XY → Z, XZ → Y, YZ → X 1:1:1 K1=XY, K2 = XZ,
- 53. Związki trójargumentowe Kardynalność Dopuszczalne zależności 1:1:1 każda M:1:1 X → Y, X → Z, Y →
- 54. Związki wieloargumentowe R(X1, X2, … , Xn) U = {X1, X2, … , Xn} U -
- 55. Związki wieloargumentowe Twierdzenie W związku n-argumentowym R(X1, X2, … , Xn) ze zbiorem F zależności funkcyjnych
- 56. Związki wieloargumentowe Dowód U – {Xi, Xj } → Xi ⇒ U – {Xi} → Xi
- 57. ZWIĄZKI TRÓJARGUMENTOWE R(X, Y, Z) XY→Z, XZ→Y, YZ→X Narzucana zależność: X→Z X→Z ∧ XZ→Y ⇒ X→Y
- 58. ZWIĄZKI TRÓJARGUMENTOWE R(X, Y, Z) XY→Z, XZ→Y Narzucana zależność: X→Z X→Z ∧ XZ→Y ⇒ X→Y Nowy
- 60. Скачать презентацию


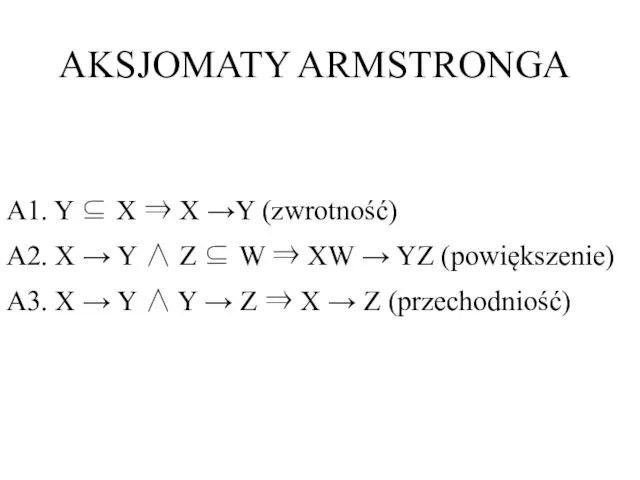


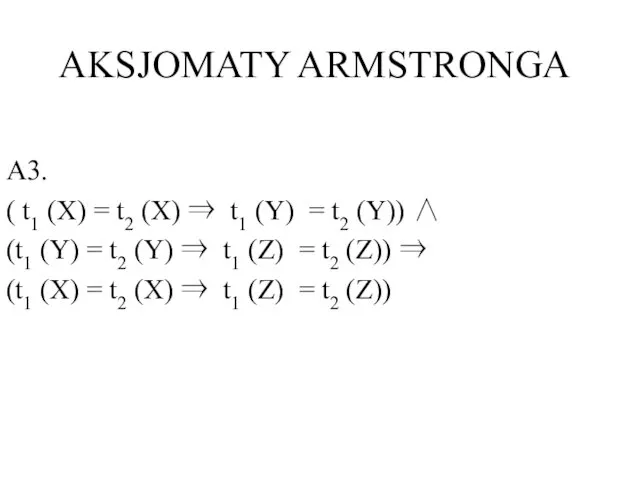














































 Физический диктант по магнитному полю
Физический диктант по магнитному полю Электроэнергетика Беларуси
Электроэнергетика Беларуси Презентация к логопедическому занятию в старшей группе В гостях у старичка - Лесовичка ( по теме Дикие животные).
Презентация к логопедическому занятию в старшей группе В гостях у старичка - Лесовичка ( по теме Дикие животные). План SMM поддержки кампании AXE247
План SMM поддержки кампании AXE247 Ship's dimensions and types of ships
Ship's dimensions and types of ships ОНИРС ОТЧЁТ 2021
ОНИРС ОТЧЁТ 2021 Religie świata
Religie świata Письмо с фронта
Письмо с фронта Михаил Михайлович Пришвин (1873-1954)
Михаил Михайлович Пришвин (1873-1954) Повторение курса физики за 7 класс
Повторение курса физики за 7 класс Неформальная конференция Печа-куча
Неформальная конференция Печа-куча Клиникалық жағдай. Anamnesis morbi
Клиникалық жағдай. Anamnesis morbi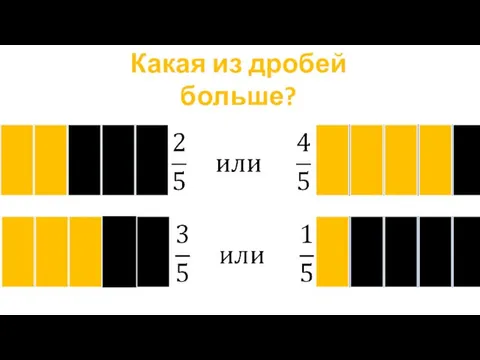 Сравнение дробей
Сравнение дробей Иммунологические особенности заболеваний почек
Иммунологические особенности заболеваний почек Общие сведения о радиоэлектронном оборудовании вертолета МИ-8АМТ
Общие сведения о радиоэлектронном оборудовании вертолета МИ-8АМТ Technology. How can you comment the quotes?
Technology. How can you comment the quotes? Союз как часть речи
Союз как часть речи Экономика потребителя
Экономика потребителя Основы разработки дополнительных общеобразовательных (общеразвивающих) программ
Основы разработки дополнительных общеобразовательных (общеразвивающих) программ Творческие работы учеников 1 б класса .Конкурс на лучшую новогоднюю игрушку.2 четверть
Творческие работы учеников 1 б класса .Конкурс на лучшую новогоднюю игрушку.2 четверть Keyon Process Co., LTD. Справка о компании
Keyon Process Co., LTD. Справка о компании Численное моделирование теплообмена в ТВС реактора БН-1200
Численное моделирование теплообмена в ТВС реактора БН-1200 Диагностика БЛОК МПСУиД САУТ-ЦМ/485
Диагностика БЛОК МПСУиД САУТ-ЦМ/485 Презентация Дикие животные Диск
Презентация Дикие животные Диск Сервировка стола. Изделия Салфетница
Сервировка стола. Изделия Салфетница Дидактические игры и упражнения для развития мелкой моторики рук и пальцев
Дидактические игры и упражнения для развития мелкой моторики рук и пальцев Shock. Etiology, pathogenesis, intensive therapy
Shock. Etiology, pathogenesis, intensive therapy Числовые неравенства
Числовые неравенства