Действия над комплексными числами
в алгебраической форме
Сложение, вычитание, умножение комплексных
чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Даны комплексные числа z1 = 2 + 3i, z2 = 5 – 7i. Найти:
а) z1 + z2; б) z1 – z2; в) z1z2.
Решение.
а) z1 + z2 = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i =
= (2 + 5) + (3i – 7i) = 7 – 4i;
б) z1 – z2 = (2 + 3i) – (5 – 7i) = 2 + 3i – 5 + 7i =
= (2 – 5) + (3i + 7i) = – 3 + 10i;
в) z1z2 = (2 + 3i)(5 – 7i) = 10 – 14i + 15i – 21i2 =
=10 – 14i + 15i + 21 = (10 + 21) + (– 14i + 15i) = 31 + i
(здесь учтено, что i2 = – 1).








 Задачи на движение. 5 класс
Задачи на движение. 5 класс Урок по теме Доли. Обыкновенные дроби.
Урок по теме Доли. Обыкновенные дроби. Математическая викторина
Математическая викторина Презентация к исследовательской работе Как нарисовать многоконечную звезду
Презентация к исследовательской работе Как нарисовать многоконечную звезду математический КВН
математический КВН Решение текстовых задач Учебно-методическое пособие
Решение текстовых задач Учебно-методическое пособие Подготовка к ЕГЭ по теме Свойства логарифмов
Подготовка к ЕГЭ по теме Свойства логарифмов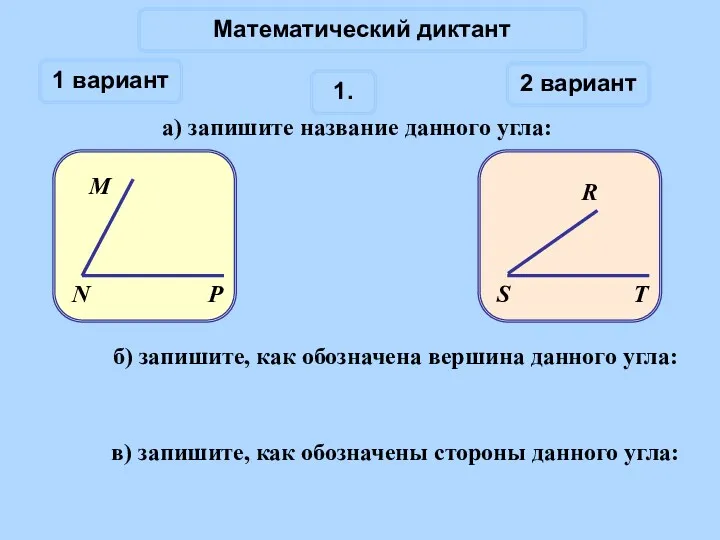 Презентация Угол
Презентация Угол Урок по теме Функция у-кх2, ее свойства и график.
Урок по теме Функция у-кх2, ее свойства и график. Математика ГИА 2014 Прототип 5
Математика ГИА 2014 Прототип 5 Презентации учеников к проекту Все тайное становиться явным
Презентации учеников к проекту Все тайное становиться явным презентация к уроку по теме :проценты (5 класс).
презентация к уроку по теме :проценты (5 класс). Положительные и отрицательные числа
Положительные и отрицательные числа Урок Противоположные числа
Урок Противоположные числа Своя игра
Своя игра Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Сложение чисел с разными знаками, 6 класс
Сложение чисел с разными знаками, 6 класс Квадратичная функция презентация
Квадратичная функция презентация Методическая разработка урока в 5 классе по теме Площадь Единицы измерения площади
Методическая разработка урока в 5 классе по теме Площадь Единицы измерения площади Математический калейдоскоп по теме:Десятичные дроби 5 класс
Математический калейдоскоп по теме:Десятичные дроби 5 класс Урок + презентация Равносильность уравнений 11класс.
Урок + презентация Равносильность уравнений 11класс. Умножение многочлена на одночлен
Умножение многочлена на одночлен В помощь учителям математики для подготовки к ОГЭ по математике
В помощь учителям математики для подготовки к ОГЭ по математике Среднее арифметическое
Среднее арифметическое Презетация для внеклассного занятия по математике, 5 класс
Презетация для внеклассного занятия по математике, 5 класс Обыкновенные дроби
Обыкновенные дроби Исследовательская работа на уроках математики
Исследовательская работа на уроках математики презентация Производная
презентация Производная