Содержание
- 2. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Types of Stochastic
- 3. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Modeling Stock Prices
- 4. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Markov Processes (See
- 5. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Weak-Form Market Efficiency
- 6. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Example of a
- 7. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Questions What is
- 8. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Variances & Standard
- 9. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Variances & Standard
- 10. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 A Wiener Process
- 11. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Properties of a
- 12. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Taking Limits .
- 13. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Generalized Wiener Processes
- 14. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Generalized Wiener Processes
- 15. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Generalized Wiener Processes
- 16. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 The Example Revisited
- 17. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Itô Process (See
- 18. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Why a Generalized
- 19. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 An Ito Process
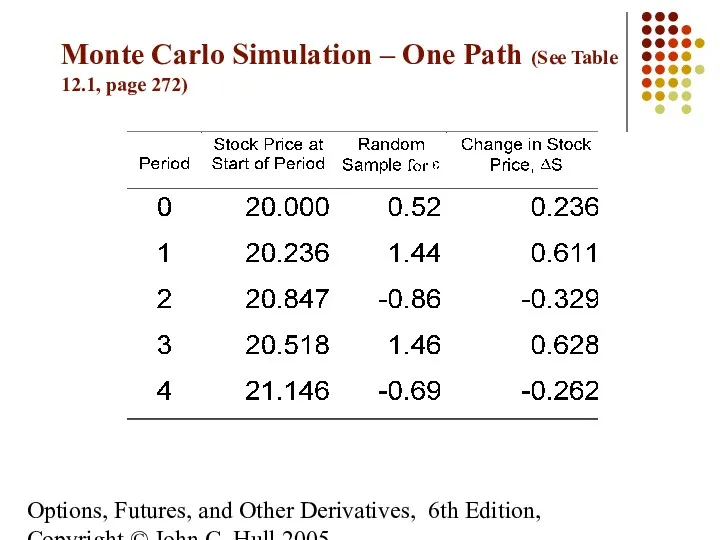
- 20. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Monte Carlo Simulation
- 21. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Monte Carlo Simulation
- 22. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Itô’s Lemma (See
- 23. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Taylor Series Expansion
- 24. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Ignoring Terms of
- 25. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Substituting for Δx
- 26. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 The ε2Δt Term
- 27. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Taking Limits
- 28. Options, Futures, and Other Derivatives, 6th Edition, Copyright © John C. Hull 2005 Application of Ito’s
- 30. Скачать презентацию


























 Международные стандарты бухгалтерской отчетности
Международные стандарты бухгалтерской отчетности Региональная бюджетная система
Региональная бюджетная система Анализ прибыли и рентабельности предприятия
Анализ прибыли и рентабельности предприятия Налоги и налогообложение в РФ. (Часть 2)
Налоги и налогообложение в РФ. (Часть 2) Лицензирование банков. Слайды
Лицензирование банков. Слайды Использование финансов в современной экономике
Использование финансов в современной экономике Банк. Кредиты. Банковские вклады. Операции с ценными бумагами
Банк. Кредиты. Банковские вклады. Операции с ценными бумагами Собственные средства кредитных организаций и их формирование
Собственные средства кредитных организаций и их формирование Организация и управление бюджетного процесса
Организация и управление бюджетного процесса Предпосылки возникновения аудита и его место в системе контроля
Предпосылки возникновения аудита и его место в системе контроля Финансы хозяйствующих субъектов
Финансы хозяйствующих субъектов Учет основных средств
Учет основных средств Asigurarea obligatorie a autovehiculelor - RCA
Asigurarea obligatorie a autovehiculelor - RCA ОТПдирект. Банк там, где удобно Вам
ОТПдирект. Банк там, где удобно Вам Финансовая отчетность сотрудников
Финансовая отчетность сотрудников Determination of the securities market and its types
Determination of the securities market and its types Понятие финансов и финансовой деятельности государства
Понятие финансов и финансовой деятельности государства Валютный курс, факторы его определяющие. (Тема 2)
Валютный курс, факторы его определяющие. (Тема 2) Финансовое планирование и прогнозирование. Бюджетирование
Финансовое планирование и прогнозирование. Бюджетирование Учет государственных ценных бумаг
Учет государственных ценных бумаг Ўзбекистон Республикаси Марказий банки
Ўзбекистон Республикаси Марказий банки Доходы населения и уровень жизни
Доходы населения и уровень жизни Республиканские и местные налоги и сборы
Республиканские и местные налоги и сборы Диагностика драгоценных металлов
Диагностика драгоценных металлов Налоговый калькулятор по расчету налоговой нагрузки
Налоговый калькулятор по расчету налоговой нагрузки Медицинское страхование как форма социальной защиты населения в области охраны здоровья
Медицинское страхование как форма социальной защиты населения в области охраны здоровья Электронные валюты
Электронные валюты Страхование раритетных автомобилей
Страхование раритетных автомобилей