Автоматика и управление. Тема 3. Временные характеристики ЛСС. Лекция 3. Типовые входные сигналы презентация
Содержание
- 2. 3.1. Типовые входные сигналы: единичный импульс и единичная ступенчатая функция Помимо передаточной функции, динамические свойства ЛСС
- 3. 3.1.1. Единичная ступенчатая функция Единичной ступенчатой функцией называется функция, определяемая равенством:
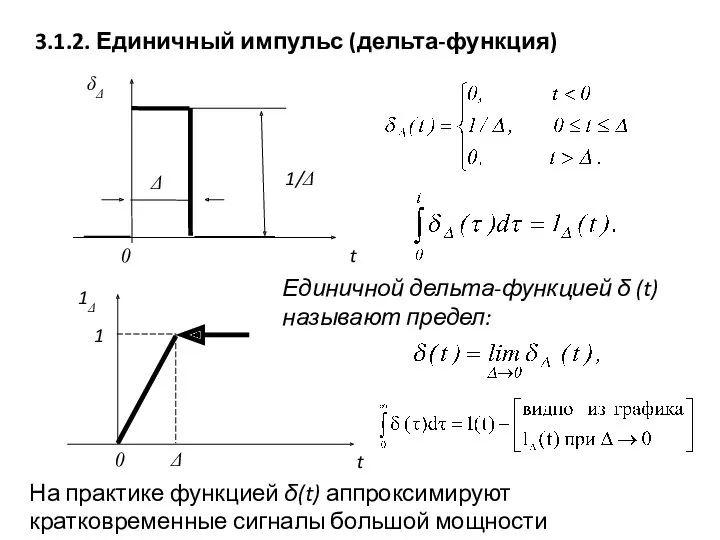
- 4. 3.1.2. Единичный импульс (дельта-функция) Единичной дельта-функцией δ (t) называют предел: На практике функцией δ(t) аппроксимируют кратковременные
- 5. Теорема Лопита́ля (также правило Бернулли — Лопиталя) — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0
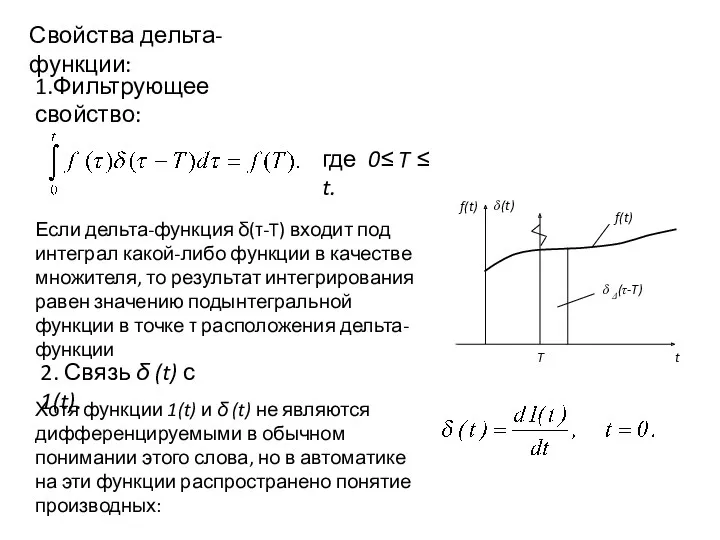
- 6. Свойства дельта-функции: 1.Фильтрующее свойство: где 0≤ T ≤ t. 2. Связь δ (t) с 1(t). Хотя
- 7. 3.2. Весовая функция одномерной ЛСС: определение; интеграл Дюамеля; аналитическое представление; общие свойства. 3.2.1. Определение весовой функции
- 8. 3.2.2. Интеграл Дюамеля Весовая функция g(t) однозначно определяет выходной сигнал ЛСС y(t) для любого входного сигнала
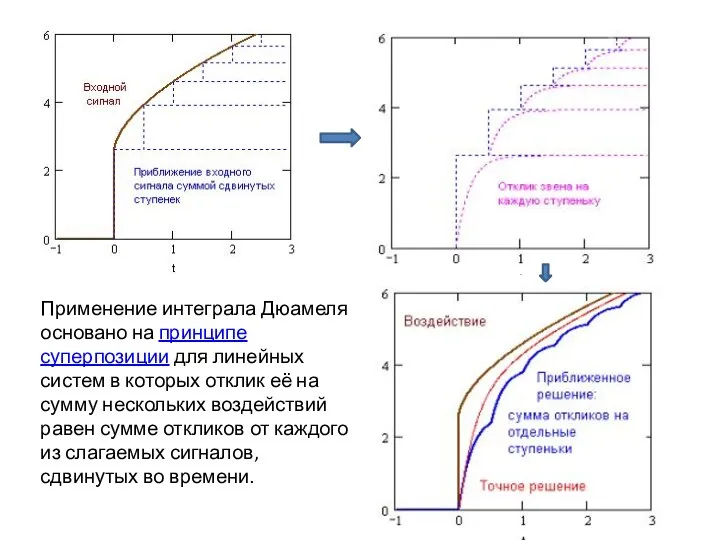
- 9. Применение интеграла Дюамеля основано на принципе суперпозиции для линейных систем в которых отклик её на сумму
- 10. 1. В том случае, если система включается в произвольный момент времени не равный нулю, т.е. t0
- 11. 3.2.3. Переход от изображения весовой функции к ее оригиналу Аналитическое представление весовой функции ЛСС можно получить
- 12. Теорема разложения Если изображение функции f(t) является рациональной функцией вида причем степень полинома числителя меньше или
- 13. Положим, что F(p) = Ф(p), тогда f(t) = g(t), следовательно: g(t)=C0δ(t)+ ,для t>0, g(t)=0, для t≤0.
- 14. Если характеристическое уравнение АС содержит кратные корни, то получение оригинала весовой функции g(t) по теореме разложения
- 15. 3.2.4. Общие свойства весовых функций ЛCC По передаточной функции ЛСС можно определить начальное и конечное значения
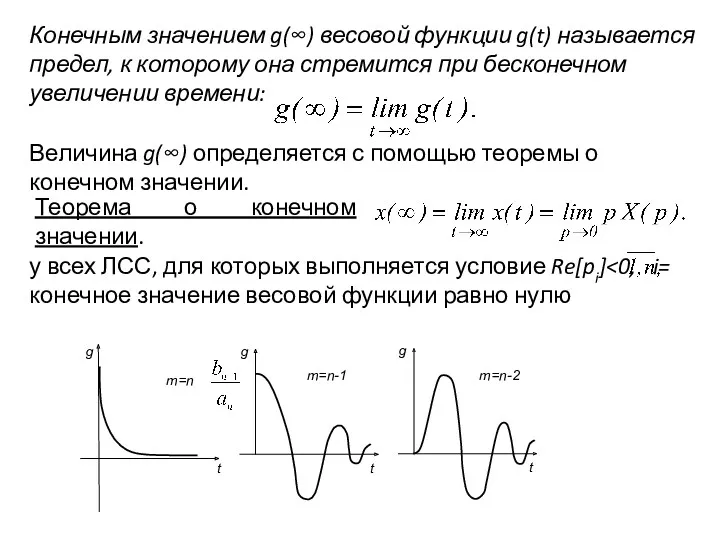
- 16. Конечным значением g(∞) весовой функции g(t) называется предел, к которому она стремится при бесконечном увеличении времени:
- 17. 3.3. Переходная функция одномерной ЛСС: определение, аналитическое представление, общие свойства 3.3.1. Определение переходной функции Для одномерной
- 18. Действительно, для ЛСС справедливо выражение: Y(p) = X(p)Ф(p). Пусть x(t) = 1(t), тогда y(t) = h(t),
- 19. Переходная и весовая функции ЛС АС однозначно связаны равенствами Переходная функция ЛСС равна интегралу от весовой
- 20. 3.3.2. Аналитическое представление переходной функции Аналитическое представление переходной функции можно получить на основании интеграла Дюамеля либо
- 21. 1 Для t>0 h(t) является линейной комбинацией постоянной составляющей и экспонент, показателями которых являются полюса передаточной
- 22. 3.3.3. Общие свойства переходных функций По передаточной функции ЛСС можно определить начальное и конечное значения переходной
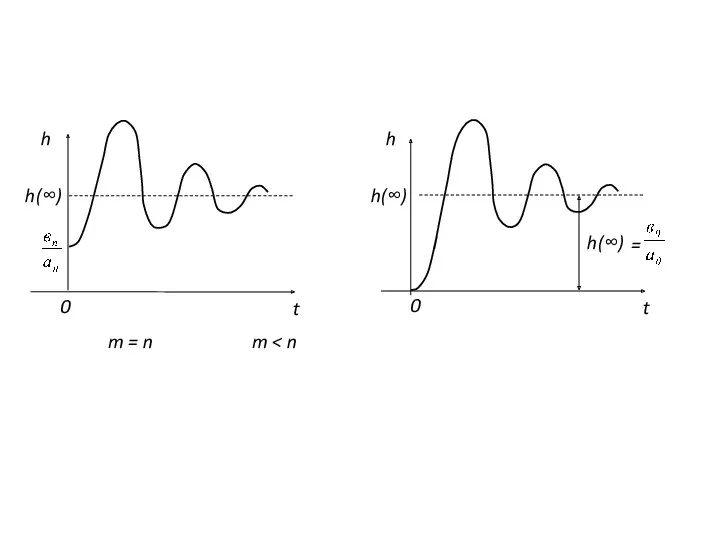
- 23. Следствия: 1. Если m=n то h(0+)= 2. Если m≤ n-1 то h(0+)= в зависимости от соотношения
- 24. m = n m
- 25. 3.4. Весовые и переходные функции элементарных динамических звеньев Усилительное звено Оператор усилительного звена имеет вид: a0
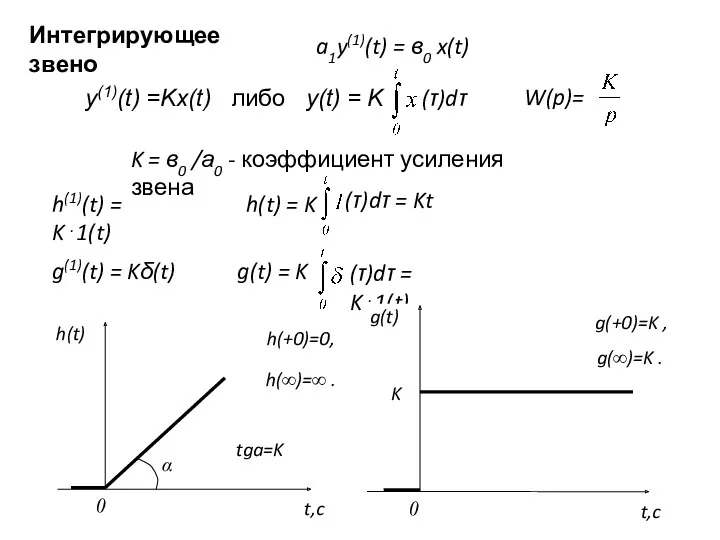
- 26. Интегрирующее звено a1y(1)(t) = в0 x(t) y(1)(t) =Kx(t) либо y(t) = K (τ)dτ K = в0
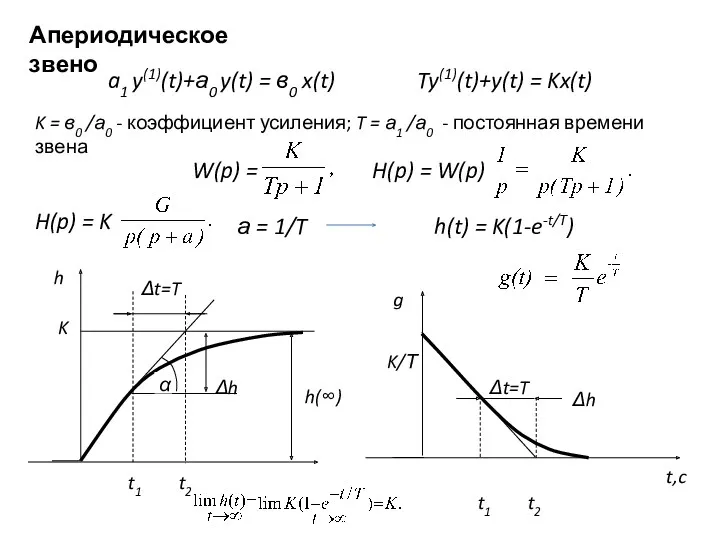
- 27. Апериодическое звено a1 y(1)(t)+а0 y(t) = в0 x(t) Ty(1)(t)+y(t) = Kx(t) K = в0 /а0 -
- 28. tga =
- 29. Инерционное звено второго порядка a2y(2)(t)+а1y(1)(t)+а0y(t) = в0 x(t) T2y(2)(t)+2Tξ y(1)(t)+y(t)=Kx(t) K = в0 /а0 - коэффициент
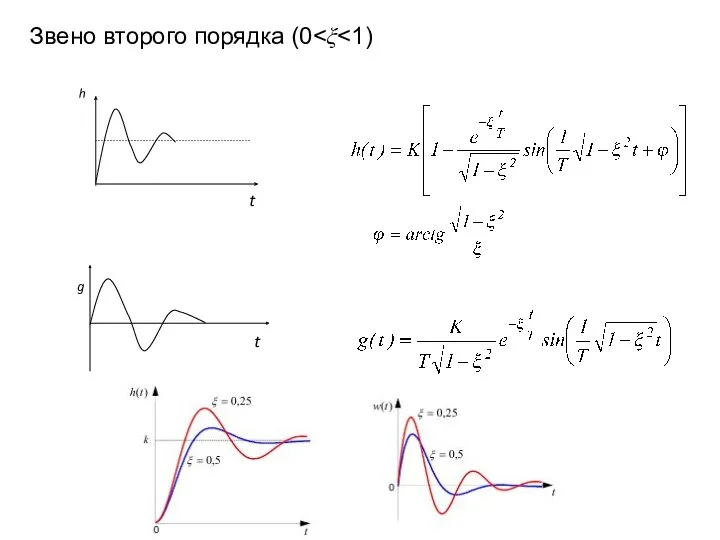
- 30. Звено второго порядка (0 h t g t
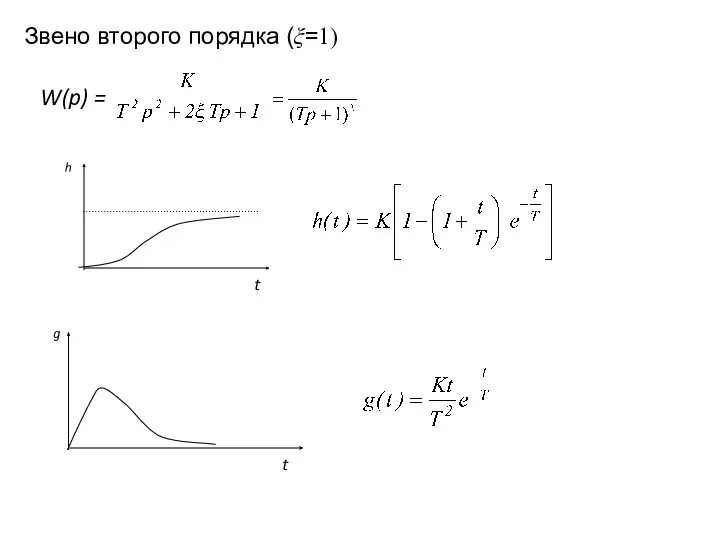
- 31. Звено второго порядка (ξ=1) W(p) = h t g t
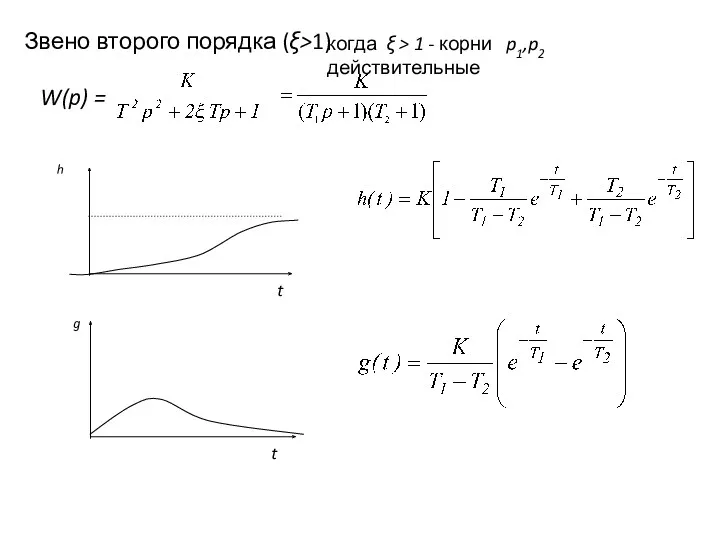
- 32. Звено второго порядка (ξ>1) W(p) = когда ξ > 1 - корни p1,p2 действительные h g
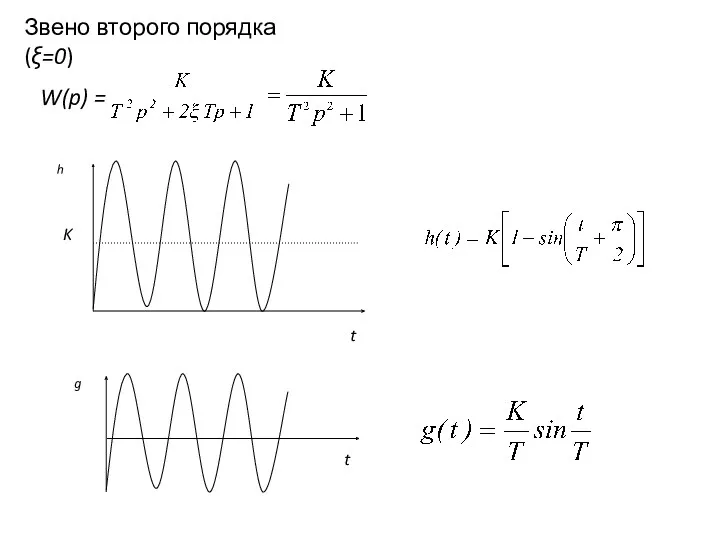
- 33. Звено второго порядка (ξ=0) W(p) = K t t
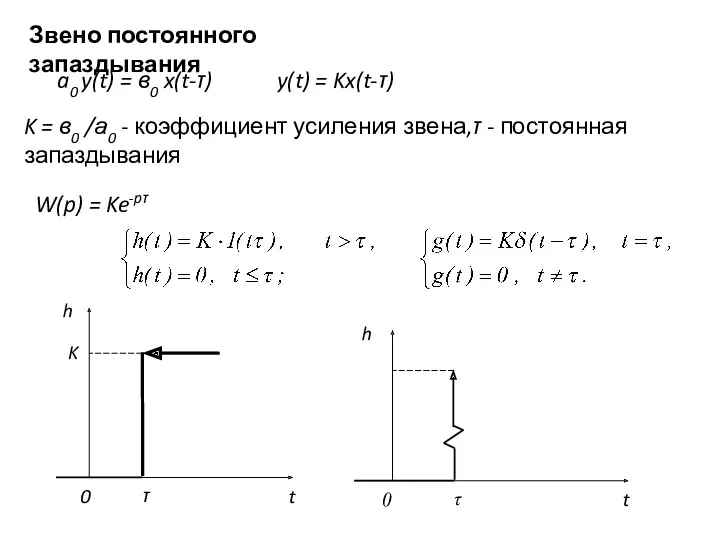
- 34. Звено постоянного запаздывания a0 y(t) = в0 x(t-τ) y(t) = Kx(t-τ) K = в0 /а0 -
- 35. Дифференцирующие и форсирующие звенья a0 y(t) = в1 x(1)(t) y(t) = Kx(1)(t) K = в1 /а0
- 37. Скачать презентацию



















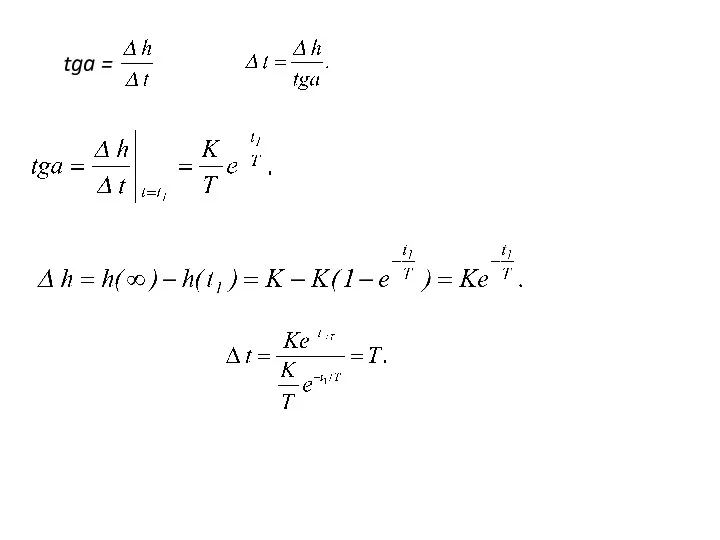


 Теплопроводность. Нестационарная теплопроводность. (Тема 4. Лекции 16,17)
Теплопроводность. Нестационарная теплопроводность. (Тема 4. Лекции 16,17) Теплові двигуни
Теплові двигуни Физико-технические основы электроэнергетики. Лекция 10
Физико-технические основы электроэнергетики. Лекция 10 Работа и энергия. Механическая работа. Мощность
Работа и энергия. Механическая работа. Мощность Линзы. Построение изображений, даваемых линзой.
Линзы. Построение изображений, даваемых линзой. Курс физики
Курс физики Первый искусственный спутник Земли
Первый искусственный спутник Земли Принцип неопределённости Гейзенберга 1927
Принцип неопределённости Гейзенберга 1927 Распространяющиеся в пространстве возмущения электромагнитного поля
Распространяющиеся в пространстве возмущения электромагнитного поля Презентация к уроку физики Электрический ток. Источники тока
Презентация к уроку физики Электрический ток. Источники тока Геоцентрическая система мира
Геоцентрическая система мира Прямой чистый изгиб. Поперечный плоский изгиб
Прямой чистый изгиб. Поперечный плоский изгиб Камера-обскура. Интересные факты
Камера-обскура. Интересные факты магнитные явления
магнитные явления Haemodynamics Haemorheology
Haemodynamics Haemorheology Электрическое освещение. Лекция 3
Электрическое освещение. Лекция 3 Деление ядер урана. Цепные ядерные реакции
Деление ядер урана. Цепные ядерные реакции Физические основы высоких технологий. (Колебания и волны)
Физические основы высоких технологий. (Колебания и волны) Электрический заряд. Дискретность электрического заряда
Электрический заряд. Дискретность электрического заряда Колесо с резиновыми спицами
Колесо с резиновыми спицами Силы в природе (7 класс)
Силы в природе (7 класс) Теория автоматического управления
Теория автоматического управления Физика Солнца
Физика Солнца Основные требования и допуски при финальной сборке. Виды и методики измерения
Основные требования и допуски при финальной сборке. Виды и методики измерения Физические явления
Физические явления Напряженно-деформированное состояние в точке
Напряженно-деформированное состояние в точке Средства механизации строительства
Средства механизации строительства Диэлектриктер. Диэлектриктердің қасиеттері
Диэлектриктер. Диэлектриктердің қасиеттері