Содержание
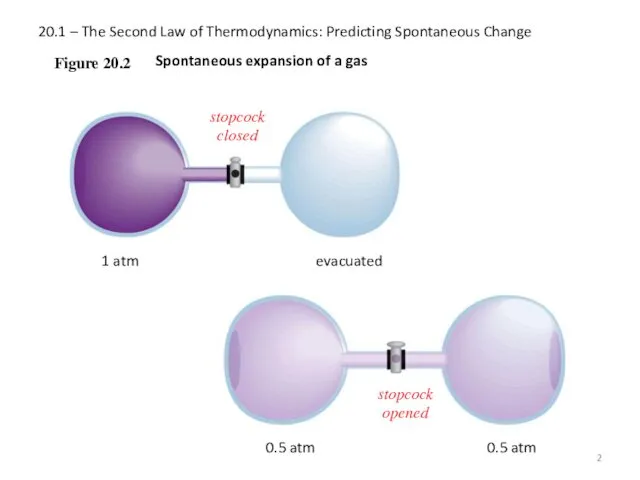
- 2. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.2 1 atm evacuated Spontaneous
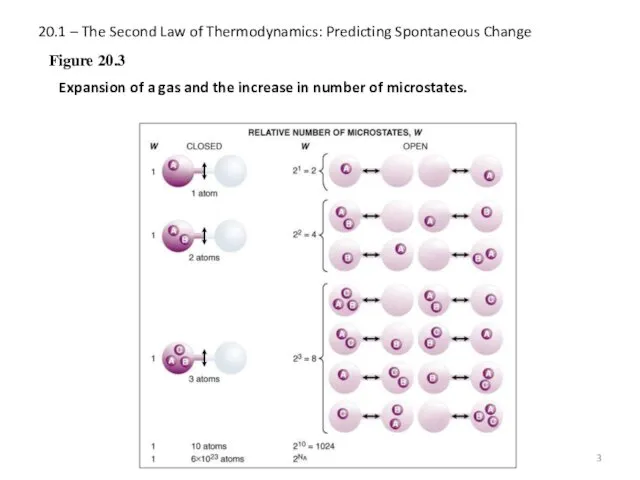
- 3. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.3 Expansion of a gas
- 4. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change 1877 Ludwig Boltzman S = k
- 5. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change The third law of thermodynamics. A
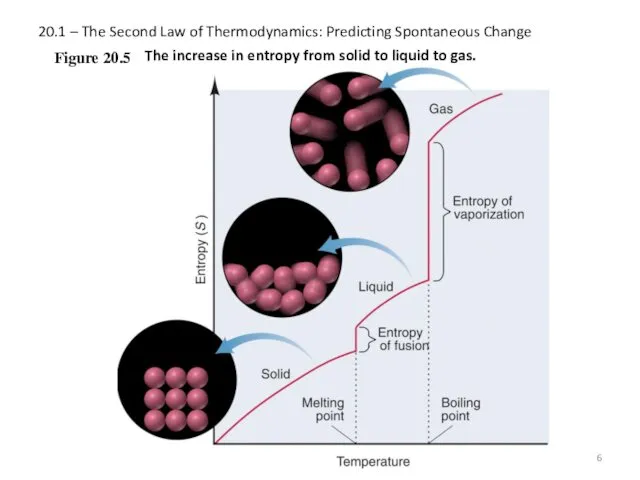
- 6. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.5 The increase in entropy
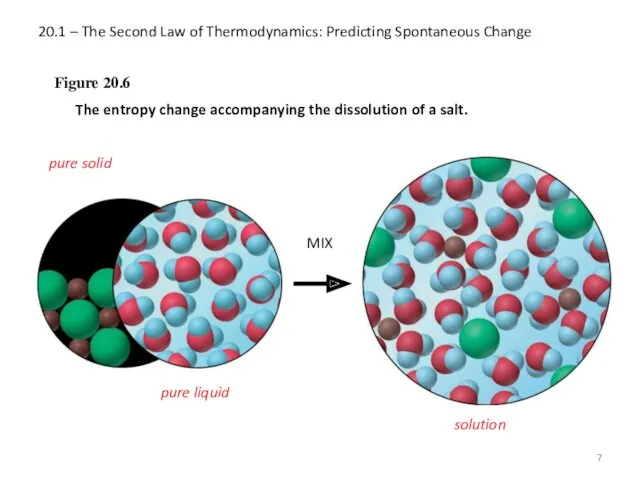
- 7. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.6 The entropy change accompanying
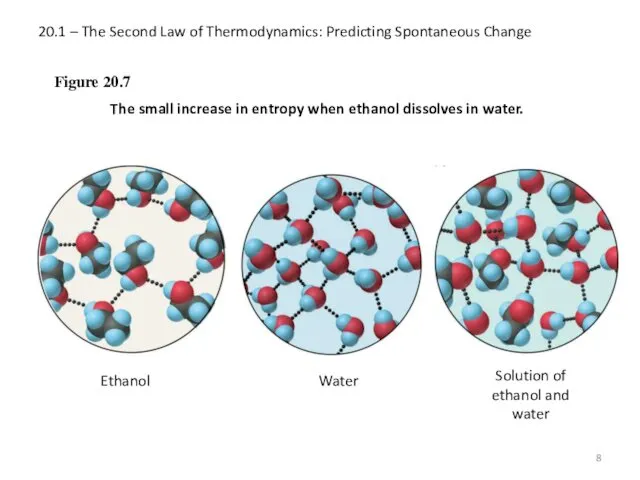
- 8. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.7 The small increase in
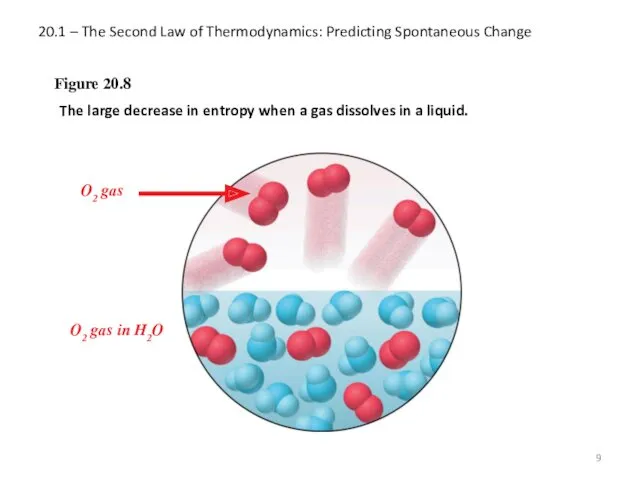
- 9. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.8 The large decrease in
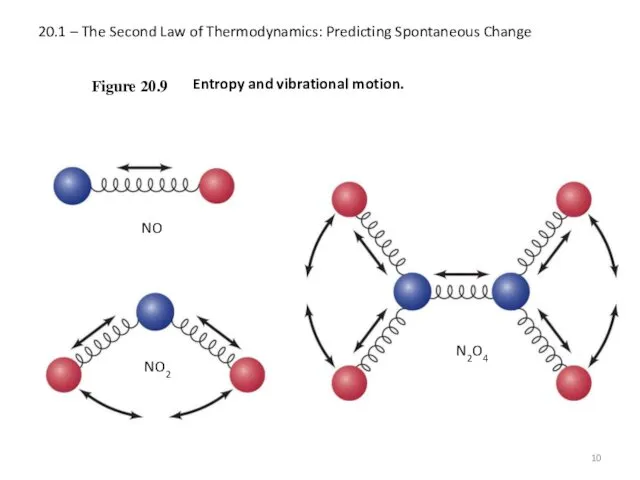
- 10. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Figure 20.9 NO Entropy and vibrational
- 11. 20.1 – The Second Law of Thermodynamics: Predicting Spontaneous Change Sample Problem 20.1: SOLUTION: Predicting Relative
- 12. 20.2 – Calculating the Change in Entropy of a Reaction Sample Problem 20.2: Calculating the Standard
- 13. 20.2 – Calculating the Change in Entropy of a Reaction Sample Problem 20.3: SOLUTION: Determining Reaction
- 14. 20.3 – Entropy, Free Energy, and Work Sample Problem 20.4: SOLUTION: Calculating ΔG0 from Enthalpy and
- 15. 20.3 – Entropy, Free Energy, and Work Sample Problem 20.4: Calculating ΔG0 from Enthalpy and Entropy
- 16. 20.3 – Entropy, Free Energy, and Work Sample Problem 20.5: PROBLEM: Calculating ΔG0rxn from ΔG0f Values
- 17. 20.3 – Entropy, Free Energy, and Work Sample Problem 20.6: PROBLEM: PLAN: SOLUTION: Determining the Effect
- 18. 20.3 – Entropy, Free Energy, and Work Sample Problem 20.6: Determining the Effect of Temperature on
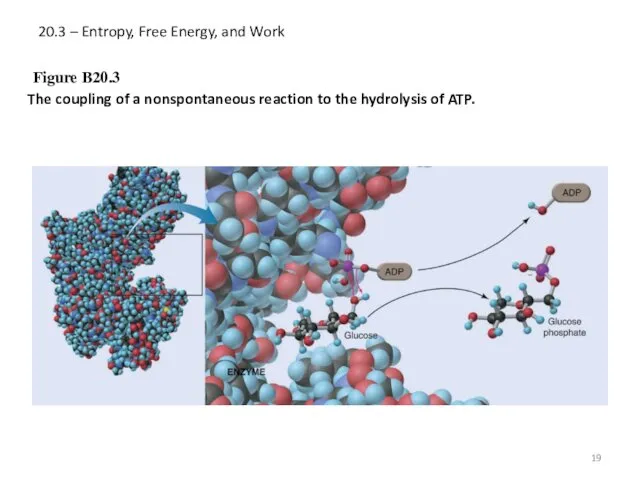
- 19. 20.3 – Entropy, Free Energy, and Work Figure B20.3 The coupling of a nonspontaneous reaction to
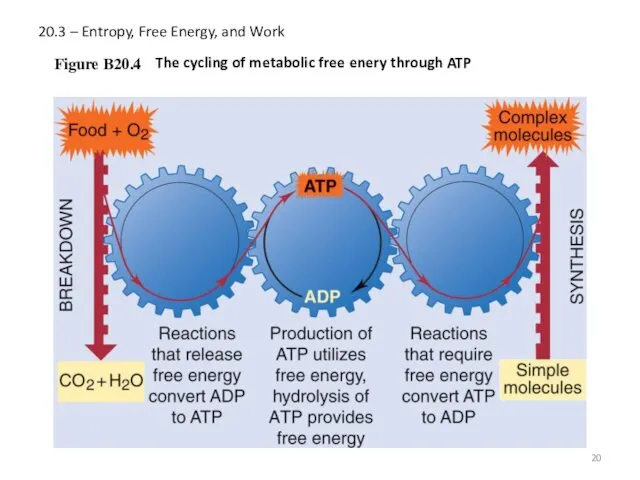
- 20. 20.3 – Entropy, Free Energy, and Work Figure B20.4 The cycling of metabolic free enery through
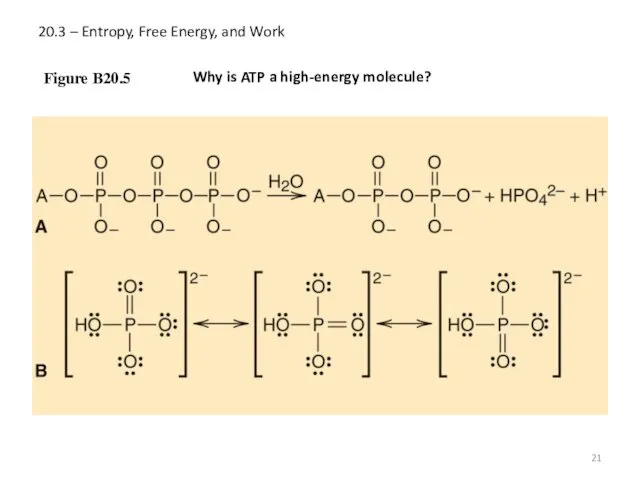
- 21. 20.3 – Entropy, Free Energy, and Work Figure B20.5 Why is ATP a high-energy molecule?
- 22. Free Energy, Equilibrium and Reaction Direction If Q/K If Q/K > 1, then ln Q/K >
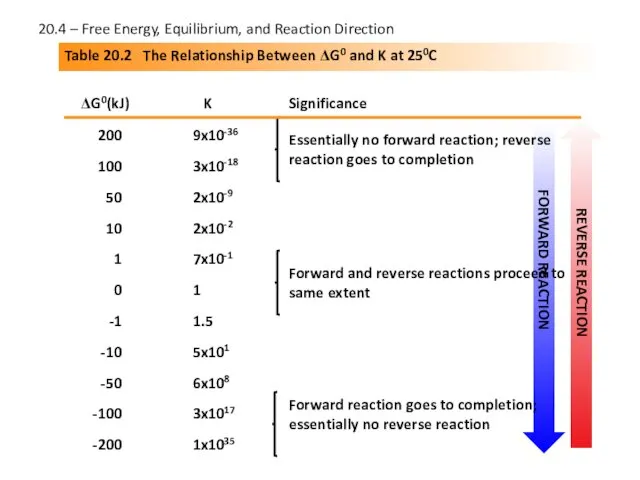
- 23. Table 20.2 The Relationship Between ΔG0 and K at 250C ΔG0(kJ) K Significance 200 100 50
- 24. Sample Problem 20.7: PROBLEM: Calculating ΔG at Nonstandard Conditions The oxidation of SO2, which we considered
- 25. SOLUTION: Sample Problem 20.7: Calculating ΔG at Nonstandard Conditions continued (2 of 3) (a) Calculating K
- 27. Скачать презентацию













 Формирование северного сияния
Формирование северного сияния Теория автоматического управления
Теория автоматического управления Акустоелектроніка. Основні принципи та уявлення
Акустоелектроніка. Основні принципи та уявлення Равновесие пространственной системы сил. (Лекция 3)
Равновесие пространственной системы сил. (Лекция 3) Атомы и ионы
Атомы и ионы Презентация к уроку Диффузия в газах, жидкостях и твёрдых телах. Движение молекул
Презентация к уроку Диффузия в газах, жидкостях и твёрдых телах. Движение молекул Скорость света
Скорость света Элементы машиноведения
Элементы машиноведения Жылулық сәулелену. Абсолют қара дене. Стефан – Больцман заңы
Жылулық сәулелену. Абсолют қара дене. Стефан – Больцман заңы Правило Ленца
Правило Ленца Дисперсия света
Дисперсия света Нормативные документы. Защита от шума. Проектирование звукоизоляции ограждающих конструкций жилых и общественных зданий
Нормативные документы. Защита от шума. Проектирование звукоизоляции ограждающих конструкций жилых и общественных зданий Самоиндукция, электромагнитная индуктивность
Самоиндукция, электромагнитная индуктивность Строение атома
Строение атома Основы молекулярно-кинетической теории
Основы молекулярно-кинетической теории Методы эффективного управления инверторами напряжения в приводах переменного тока
Методы эффективного управления инверторами напряжения в приводах переменного тока Расчёт отдельных участков контура циркуляции воды
Расчёт отдельных участков контура циркуляции воды Деформация. Виды деформаций
Деформация. Виды деформаций Расчет плотности вещества
Расчет плотности вещества Презентация для 8 класса Испарение и конденсация
Презентация для 8 класса Испарение и конденсация Классификация двигателей
Классификация двигателей Радиоактивность. 11 класс
Радиоактивность. 11 класс Кремниевые подложки интегральных схем
Кремниевые подложки интегральных схем Cummins Engine Company LTD
Cummins Engine Company LTD Змеевиковые теплообменные аппараты
Змеевиковые теплообменные аппараты Трансмиссии (силовые передачи). Бортовая коробка передач (коробка передач, раздаточная коробка, мосты) .Тема 10
Трансмиссии (силовые передачи). Бортовая коробка передач (коробка передач, раздаточная коробка, мосты) .Тема 10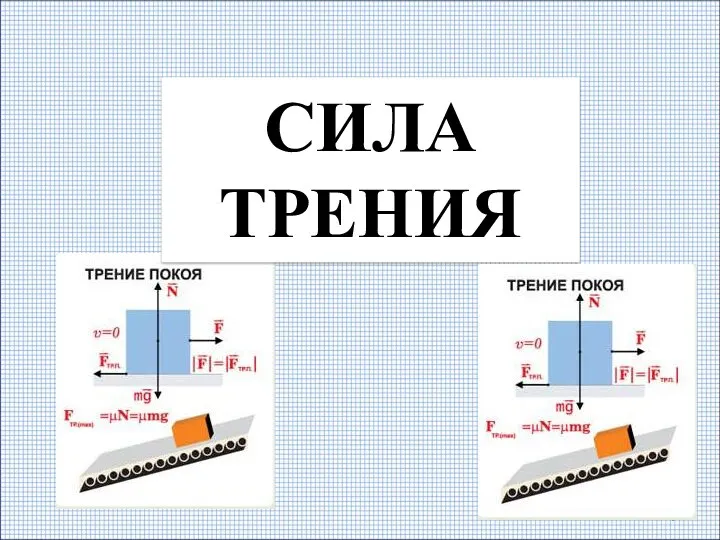 Виды силы трения
Виды силы трения Деформация тела. Сила упругости. Закон Гука
Деформация тела. Сила упругости. Закон Гука