Содержание
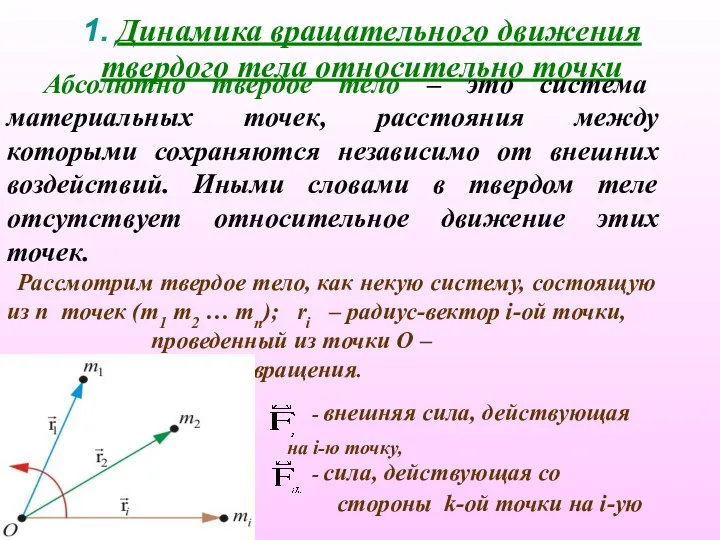
- 2. 1. Динамика вращательного движения твердого тела относительно точки Абсолютно твердое тело – это система материальных точек,
- 3. Умножим обе части векторно на Знак производной в данном случае можно вынести за знак векторного произведения
- 6. вект. (произведение силы на плечо)
- 7. C учетом новых обозначений наше уравнение: примет вид Запишем систему n уравнений для всех точек системы
- 8. Вынесем знак производной за знак суммы здесь - суммарный момент импульса твердого тела. Обозначим - результирующий
- 9. Это основной закон динамики движения твердого тела, вращающегося вокруг неподвижной точки. Уравнение моментов относительно неподвижной точки
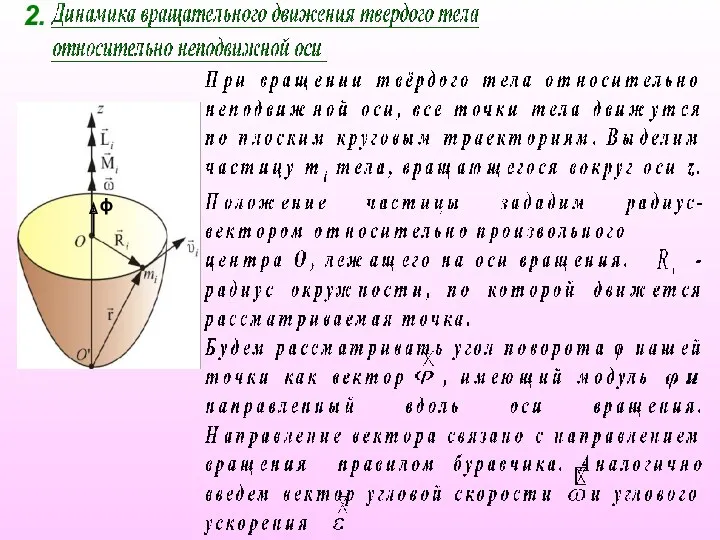
- 10. 2. ϕ
- 15. Момент импульса L твердого тела – это сумма моментов импульсов всех его материальных точек Момент импульса
- 16. 3.Расчет моментов инерции некоторых простых тел. В качестве примера вычислим момент инерции тонкого однородного стержня относительно
- 17. Вычислив подобным образом, моменты инерции всех элементов стержня, сложим их, взяв интеграл: получаем Моменты инерции некоторых
- 18. Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции Ic относительно оси, параллельной данной
- 19. Пример: стержень массой m, длиной l, вращается вокруг оси, проходящей через конец стержня (рис).
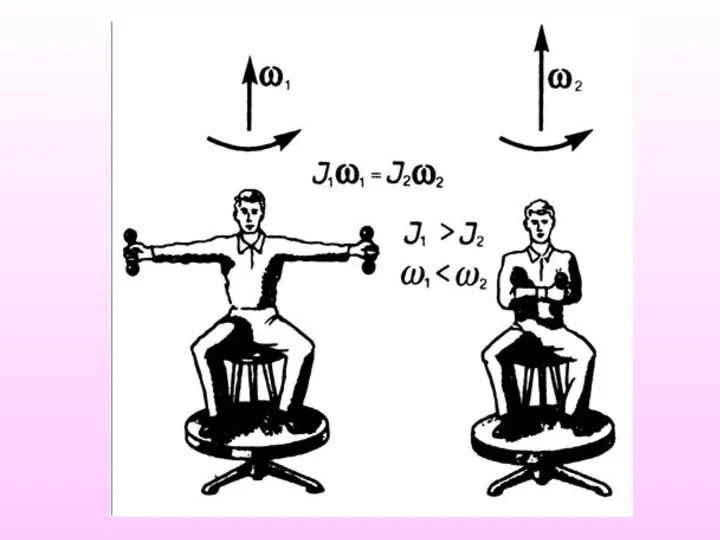
- 20. 4.Закон сохранения момента импульса Вернемся ещё раз к уравнению моментов в виде: Оно в равной степени
- 21. Если не меняется момент импульса тела (Lz), то это не означает постоянства угловой скорости: если момент
- 23. 5.Кинетическая энергия твердого тела Вычислим кинетическую энергию К тела, вращающегося вокруг неподвижной оси z с угловой
- 24. Произвольное движение твердого тела. Рассмотрим одно из простых движений абсолютно твердого тела – плоское движение. Это
- 25. В результате полная система уравнений, описыва-ющая произвольное движение абсолютно твердого тела, принимает вид: где m -
- 26. Кинетическая энергия твердого тела, совершающего поступательное движение со скоростью движения центра масс и вращательное движение с
- 27. Условия равновесия абсолютно твердого тела включают два динамических условия которые вытекают из уравнений движения, и два
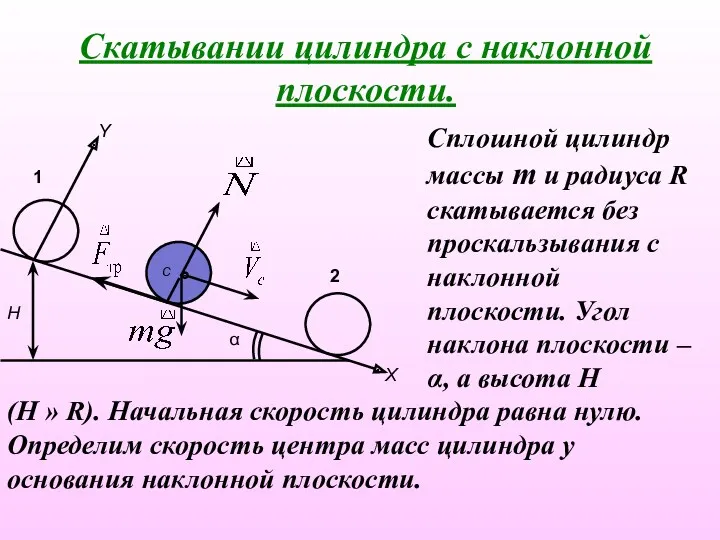
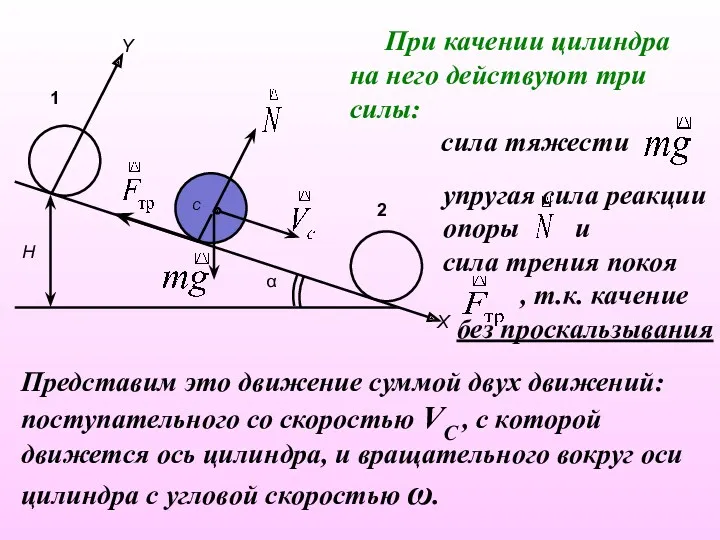
- 28. Скатывании цилиндра с наклонной плоскости. Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с
- 29. При качении цилиндра на него действуют три силы: сила тяжести упругая сила реакции опоры и сила
- 30. Эту задачу можно решить, воспользовавшись законом сохранения механической энергии. В системе, правда, присутствует сила трения, но
- 31. Рассмотрим энергию цилиндра в начальный момент — на высоте H и в конце спуска. Полная энергия
- 32. Из условия «движение без проскальзывания» имеем связь между угловой скорость и скоростью центра масс: Продифференцировав это
- 33. Спроецировав уравнение на направления осей x и y, получим два скалярных уравнения: x: mgSinα – Fтр
- 34. Учитывая всё это, уравнение моментов перепишем так: (3) Решая совместно уравнения движения(1), (2), и (3) получим
- 35. Но, как известно, её рост ограничен предельным значением: Следовательно, должно выполняться неравенство: ⅓mgSinα ≤ μmgCosα. Отсюда
- 36. Линейное ускорение цилиндра величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости
- 37. Вычислим конечную скорость поступательного движения оси цилиндра: Она совпадает с результатом, полученным выше более простым путем,
- 38. Сходство и различие линейных и угловых характеристик движения Формулы кинематики и динамики вращательного движения легко запоминаются,
- 39. Поступательное движение Вращательное движение
- 43. Скачать презентацию



































 Электрисеский ток. Сила тока.
Электрисеский ток. Сила тока. Программа элективного курса Методы и приёмы решения задач по физике
Программа элективного курса Методы и приёмы решения задач по физике Динамика негіздері
Динамика негіздері Общее устройство автомобиля
Общее устройство автомобиля Ядерный реактор. Атомная энергетика
Ядерный реактор. Атомная энергетика Закон всемирного тяготения
Закон всемирного тяготения Системно-деятельностный подход в обучении физики как основа ФГОС
Системно-деятельностный подход в обучении физики как основа ФГОС Электричество. Работа электрического тока
Электричество. Работа электрического тока Сопротивление материалов
Сопротивление материалов Механика. Механическое движение
Механика. Механическое движение Силовое поле. Работа. Энергия. Мощность
Силовое поле. Работа. Энергия. Мощность Презентация Кислород
Презентация Кислород Выяснение условия равновесия рычага
Выяснение условия равновесия рычага Физические и геологические основы сейсморазведки
Физические и геологические основы сейсморазведки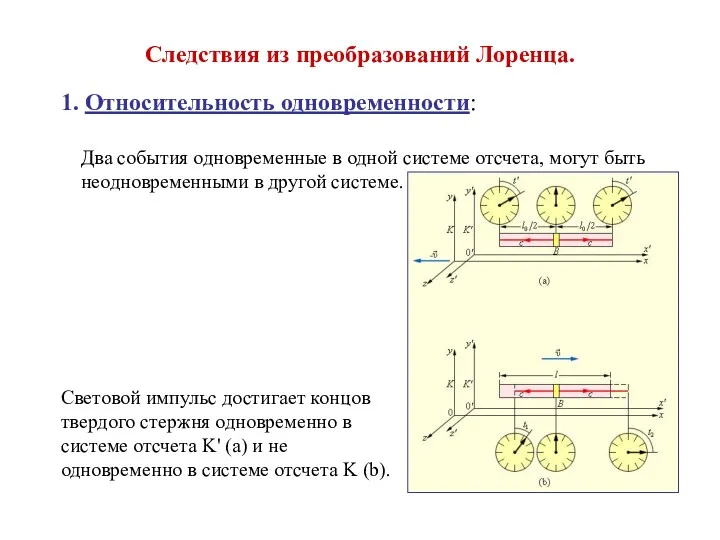 Следствия из преобразований Лоренца
Следствия из преобразований Лоренца Ерітінділердің коллигативті қасиеттері. Ерітінділер буының қысымы. Осмос қысымы
Ерітінділердің коллигативті қасиеттері. Ерітінділер буының қысымы. Осмос қысымы Thermal Energy, Chemical Energy
Thermal Energy, Chemical Energy Design and mechanical stability analysis of the interaction region for the inverse compton scattering gamma-ray source
Design and mechanical stability analysis of the interaction region for the inverse compton scattering gamma-ray source Історичні моделі будови атому
Історичні моделі будови атому Бұрандалы конвейерлер. Түрлері және қолдану аймағы
Бұрандалы конвейерлер. Түрлері және қолдану аймағы Электрооборудование автомобилей. Электростартеры. (Урок 4)
Электрооборудование автомобилей. Электростартеры. (Урок 4) Электростатика. Поле в диэлектриках
Электростатика. Поле в диэлектриках Механізація водопостачання
Механізація водопостачання Движение тела вокруг неподвижной точки. Случай Эйлера
Движение тела вокруг неподвижной точки. Случай Эйлера Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Физические основы прочности. Кристаллогеометрия деформационных процессов. (Лекция 2-3)
Физические основы прочности. Кристаллогеометрия деформационных процессов. (Лекция 2-3) Спектроскопия ядерного магнитного резонанса
Спектроскопия ядерного магнитного резонанса Реактивные двигатели
Реактивные двигатели