Динамика вращательного движения твердого тела. Основное уравнение динамики вращательного движения. Момент инерции твердого тела презентация
Содержание
- 2. На прошлом занятии разобрали импульс и энергию. Рассмотрим величину момент импульса - характеризует количество вращательного движения.
- 3. Рассмотрим изменение вектора L со временем: т.к. dr/dt =v, v направлен так же, как и p
- 4. Уравнение моментов позволяет: Найти момент силы M относительно точки O в любой момент времени t ,
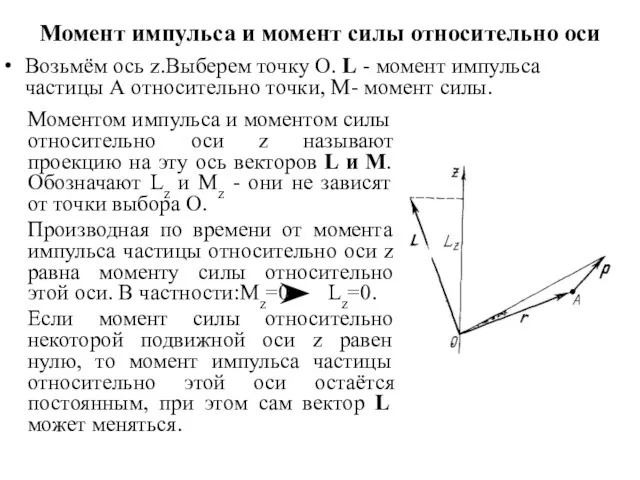
- 5. Момент импульса и момент силы относительно оси Возьмём ось z.Выберем точку О. L - момент импульса
- 6. Закон сохранения моменте импульса Выберем произвольную систему частиц. Момент импульса данной системы будет векторная сумма моментов
- 7. Момент импульса системы может изменяться под действием только суммарного момента всех внешних сил Закон сохранения импульса:
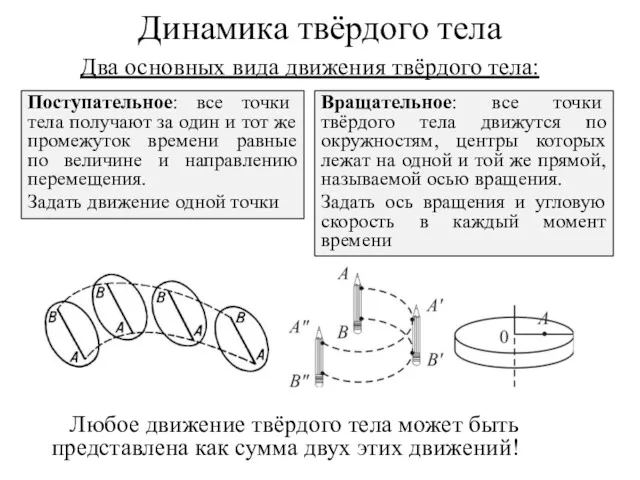
- 8. Динамика твёрдого тела Два основных вида движения твёрдого тела: Поступательное: все точки тела получают за один
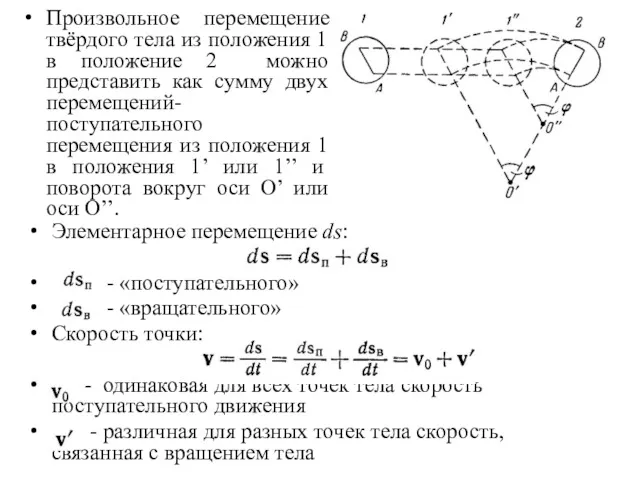
- 9. Произвольное перемещение твёрдого тела из положения 1 в положение 2 можно представить как сумму двух перемещений-
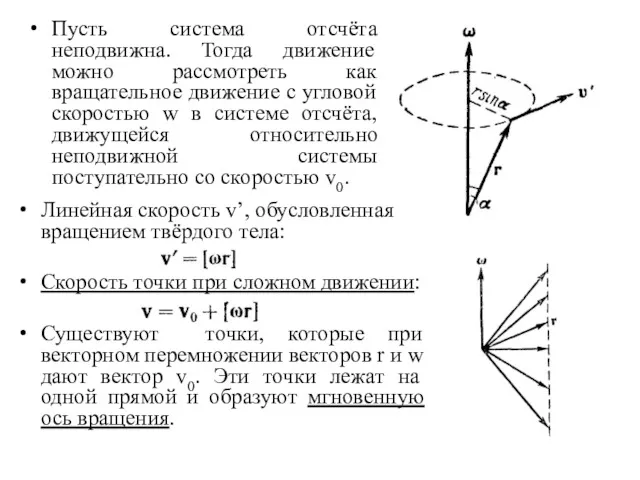
- 10. Пусть система отсчёта неподвижна. Тогда движение можно рассмотреть как вращательное движение с угловой скоростью w в
- 11. Движение твёрдого тела в общем случае определяется двумя векторными уравнениями: Уравнение движения центра масс: Уравнение моментов:
- 12. Условия равновесия твердого тела: тело будет оставаться в состоянии покоя, если нет причин, вызывающих его движение.
- 13. Вращение вокруг неподвижной оси Момент импульса твёрдого тела относительно оси вращения ОО’: где mi и pi-
- 14. Моменты инерции однородных твёрдых тел, относительно оси проходящей через центр масс: Теорема Штейнера: момент инерции I
- 15. Уравнение динамики вращения твёрдого тела: где Mz – суммарный момент всех внешних сил относительно оси вращения.
- 16. Плоское движение твёрдого тела При плоском движении центра масс твердого тела движется в определённой плоскости, неподвижной
- 18. Скачать презентацию











 Интерференция и дифракция света
Интерференция и дифракция света Тонкослойная хроматография
Тонкослойная хроматография Устройство асинхронного двигателя с короткозамкнутым ротором
Устройство асинхронного двигателя с короткозамкнутым ротором Історія електричної лампи ( Das Geschichte des Glübirne )
Історія електричної лампи ( Das Geschichte des Glübirne ) Знамя Победы – наука! Выступление на научно – практической конференции
Знамя Победы – наука! Выступление на научно – практической конференции Кривошипно-шатунный механизм
Кривошипно-шатунный механизм Отражение света. Преломление света
Отражение света. Преломление света Волновая оптика
Волновая оптика Допуски формы, расположение поверхности, шероховатость поверхности. Лекция 5
Допуски формы, расположение поверхности, шероховатость поверхности. Лекция 5 Конденсаторы. Энергия заряженного конденсатора
Конденсаторы. Энергия заряженного конденсатора кл Работа в термодинамике. 1 закон термодинамики
кл Работа в термодинамике. 1 закон термодинамики Практическая работа. Изучение машин и оборудования для расчистки озеленяемых территорий
Практическая работа. Изучение машин и оборудования для расчистки озеленяемых территорий Важіль
Важіль Диффузия вокруг нас
Диффузия вокруг нас Программа элективного курса Методы и приёмы решения задач по физике
Программа элективного курса Методы и приёмы решения задач по физике Миражи
Миражи Электромагнитная индукция
Электромагнитная индукция Применение БИК-спектроскопии при производстве, контроле качества лс и выявлении недоброкачественных и фальсифицированных лс
Применение БИК-спектроскопии при производстве, контроле качества лс и выявлении недоброкачественных и фальсифицированных лс Корпускулярно-волновой дуализм материи
Корпускулярно-волновой дуализм материи Магнитная гидродинамика
Магнитная гидродинамика Судовые устройства
Судовые устройства Ядерный реактор
Ядерный реактор Автоматизация в современном производсве
Автоматизация в современном производсве Заттың физикалық қасиеттері
Заттың физикалық қасиеттері Жидкостная хроматография
Жидкостная хроматография Магнитные свойства вещества
Магнитные свойства вещества Course of lectures Contemporary Physics: Part1
Course of lectures Contemporary Physics: Part1 The main types of lathes
The main types of lathes