Содержание
- 2. Гармонические колебания и их характерис- тики. Метод вращающегося вектора амплитуды. Гармонический осциллятор. Пружинный, физический и математический
- 3. Гармонические колебания и их характеристики Наряду с поступательным и вращательным движе-ниями тел в механике значительный интерес
- 4. в процессе колебаний, повторяются через равные про-межутки времени, которые называются периодом ко-лебания. Простейшим типом периодических колебаний
- 5. Периодически изменяющийся аргумент косинуса называется фазой колебания. За один период фаза колебания получает прираще-ние равное ,
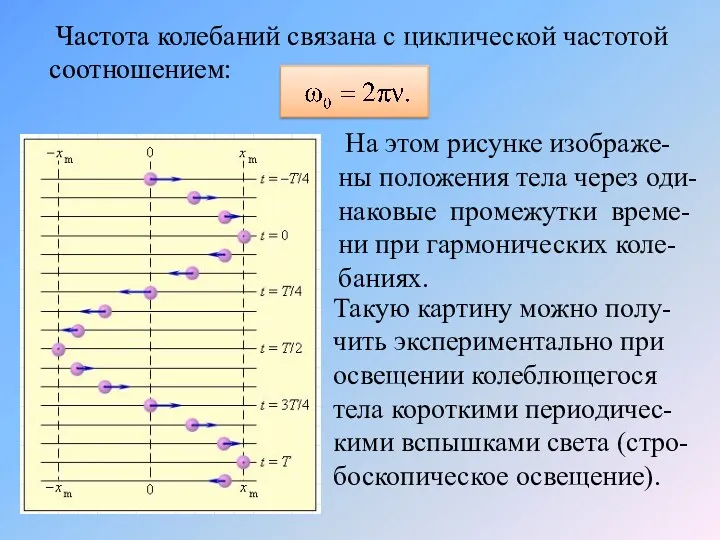
- 6. Частота колебаний связана с циклической частотой соотношением: На этом рисунке изображе-ны положения тела через оди-наковые промежутки
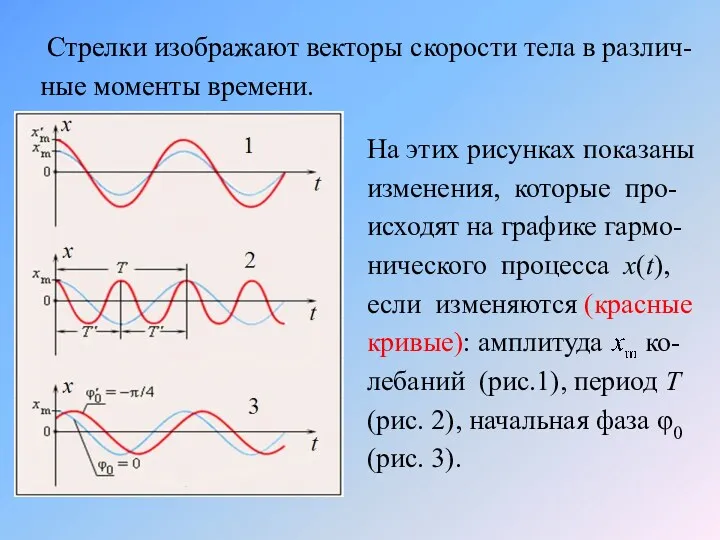
- 7. Стрелки изображают векторы скорости тела в различ-ные моменты времени. На этих рисунках показаны изменения, которые про-исходят
- 8. Колебания называются свободными (или собствен-ными), если они продолжаются неограниченно долго за счёт первоначально сообщённой кинетической или
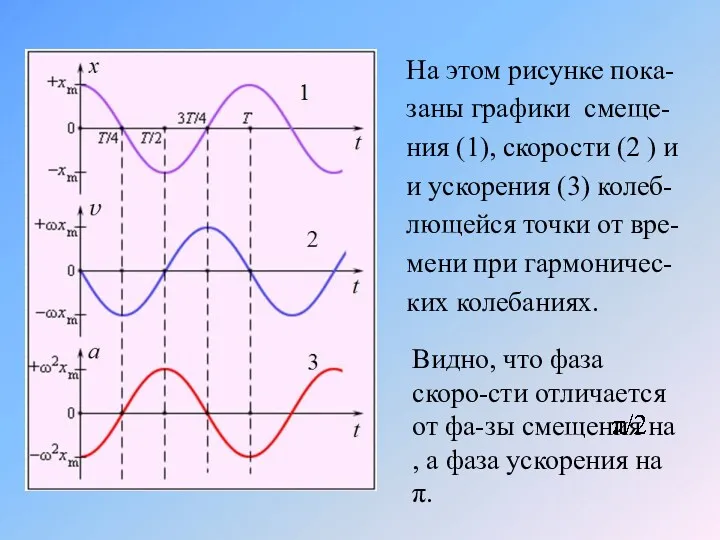
- 9. На этом рисунке пока-заны графики смеще-ния (1), скорости (2 ) и и ускорения (3) колеб-лющейся точки
- 10. Запишем выражение для ускорения в виде: Или Это уравнение называется дифференциальное ура-внение гармонических колебаний.
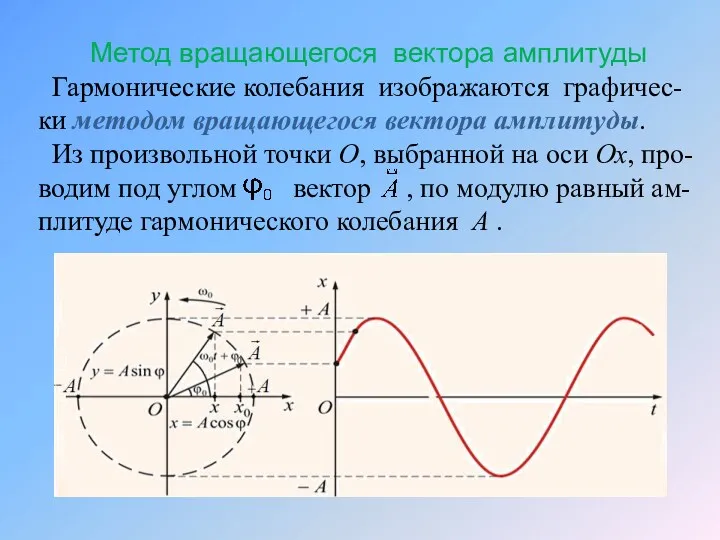
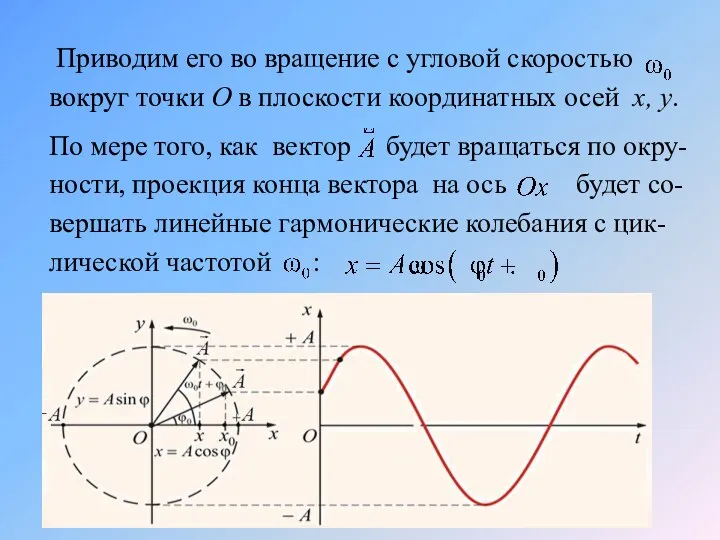
- 11. Метод вращающегося вектора амплитуды Гармонические колебания изображаются графичес-ки методом вращающегося вектора амплитуды. Из произвольной точки О,
- 12. Приводим его во вращение с угловой скоростью вокруг точки О в плоскости координатных осей x, y.
- 13. Гармонический осциллятор. Пружинный, математический и физический маятники Свободные колебания совершаются под действием внутренних сил системы после
- 14. Тело, совершающее колебания под действием ква-зиупругих сил, называют гармоническим осцил-лятором, а уравнение вида – урав-нением гармонического
- 15. Груз массы m, прикреплён- ный к горизонтальной пру- жине жёсткости k, второй конец которой закреплён неподвижно,
- 16. Откуда и Математическим маятником называют тело не-больших размеров, подвешенное на тонкой нерас-тяжимой нити, масса которой пренебрежимо
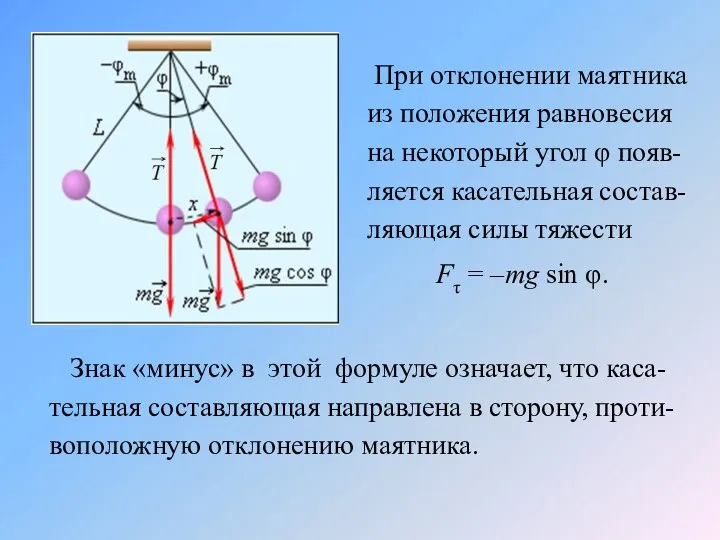
- 17. При отклонении маятника из положения равновесия на некоторый угол φ появ-ляется касательная состав-ляющая силы тяжести Fτ
- 18. Эта составляющая создаст вращающий момент В соответствии с основным законом динамики вра-щательного движения этот момент сил
- 19. Таким образом, колебания математического маятника описываются уравнением гармонического осцилля- тора. Следовательно, и Любое тело, насаженное на
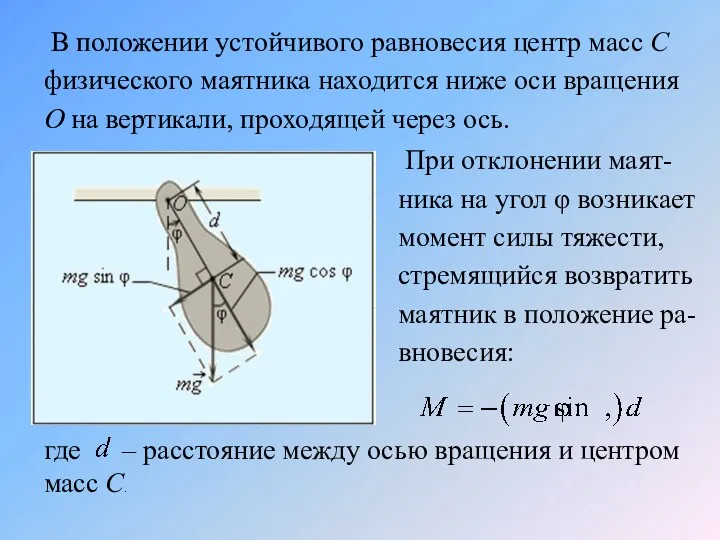
- 20. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали,
- 21. Знак «минус» в этой формуле означает, что момент сил стремится повернуть маятник в направлении, противоположном его
- 22. и основной закон динамики для вращательного движения физического маятника принимает вид: Таким образом, колебания физического маятника
- 23. Сравнивая формулы заключаем, что математический маятник с длиной , которая называется приведённая длина физического маятника, будет
- 24. если физический маятник подвесить за центр кача-ния, то его период не изменится и прежняя точка по-двеса
- 26. Превращение энергии при свободных механических колебаниях При свободных механических колебаниях кинети-ческая и потенциальная энергии тела изменяются
- 27. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих дефор-маций пружины. Для математического
- 28. Таким образом, при гармонических колебаниях происходит периодическое превращение кинети-ческой энергии в потенциальную и наоборот. Кинетическую энергию
- 29. Потенциальная энергия материальной точки, совер-шающей гармонические колебания по действием упру-гой силы Из этих формул следует, что
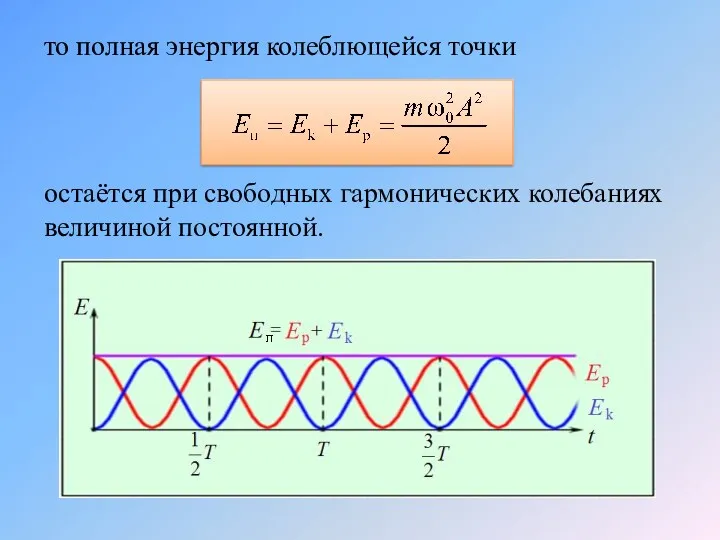
- 30. то полная энергия колеблющейся точки остаётся при свободных гармонических колебаниях величиной постоянной.
- 31. Затухающие колебания В реальных условиях любая колебательная система находится под воздействием сил трения (сопротивле-ния). При этом
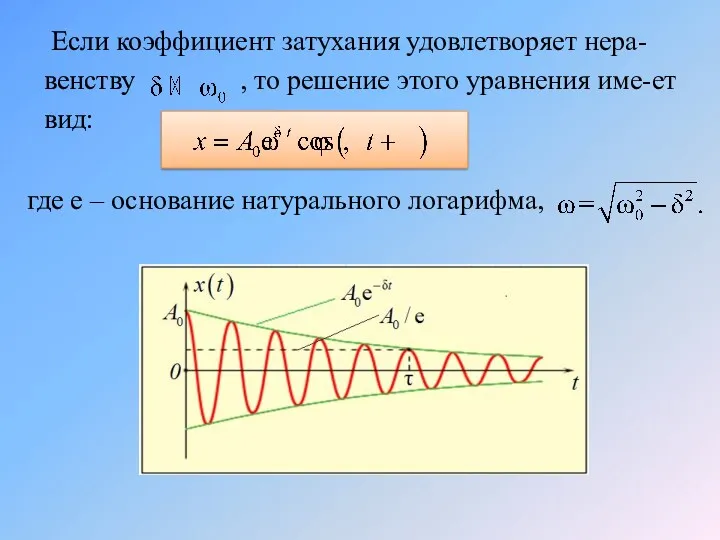
- 32. Если коэффициент затухания удовлетворяет нера-венству , то решение этого уравнения име-ет вид: где е – основание
- 33. Промежуток времени τ, в течении которого амплиту-да колебаний уменьшается в е раз, называется време-нем релаксации. Период
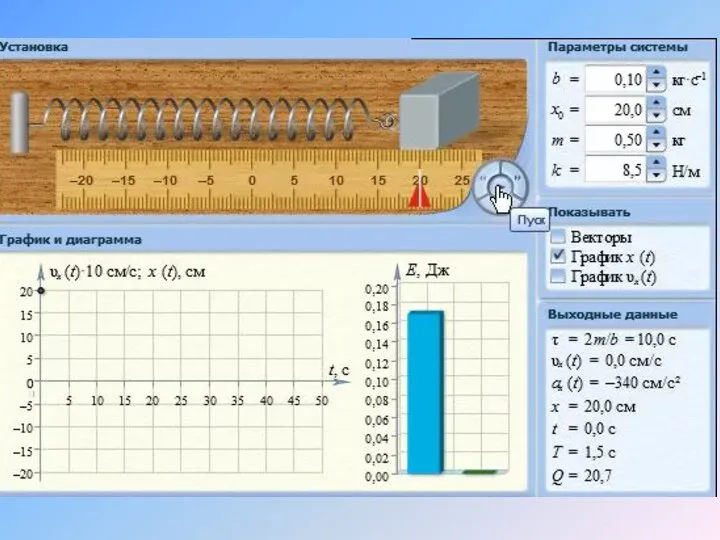
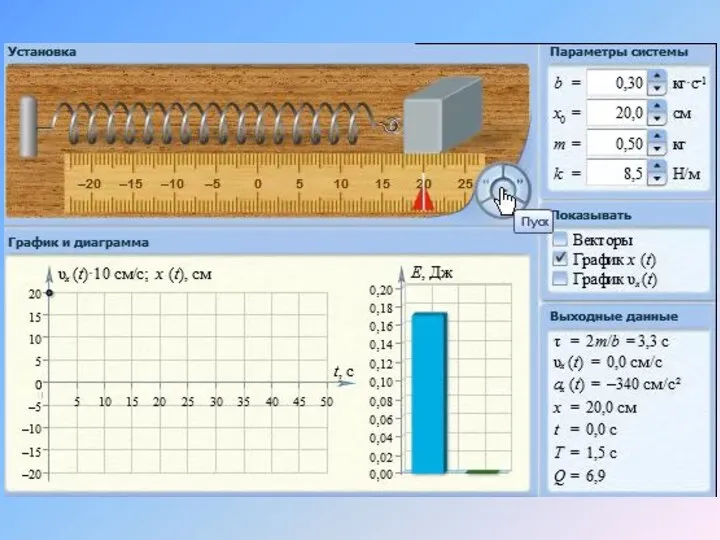
- 34. где – число колебаний, совершаемых за время ре-лаксации, – логарифмическим декрементом зату-хания. Для пружинного маятника массой
- 35. Если в это уравнение подставить величины то получим уравнение решением которого будет уравнение Важной характеристикой колебательной
- 36. Чем медленнее происходит затухание свободных колебаний, тем выше добротность колебательной системы. Добротности механических колебательных систем могут
- 37. Таким образом, добротность характеризует относи-тельную убыль энергии колебательной системы из-за наличия трения на интервале времени, равном
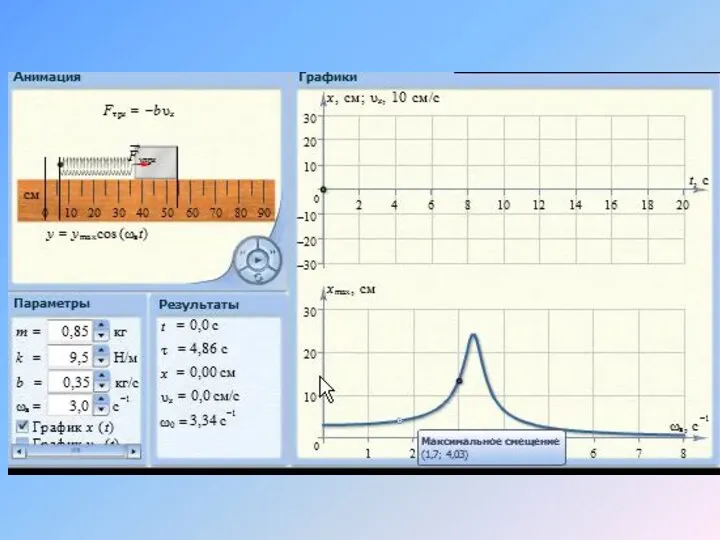
- 40. Вынужденные колебания. Резонанс Рассмотрим систему, на которую кроме упругой силы (– kx) и сил сопротивления (–
- 41. где Проанализируем зависимость амплитуды вынуж-денных колебаний от частоты вынуждающей силы и коэффициента затухания. – частота вынуждающей
- 42. – (затухания нет). С увеличением ω (но при ) амплитуда растёт и при про-исходит резкое увеличение
- 43. В реальных условиях амплитуда уста-новившихся вынужденных колебаний определя-ется условием: работа внешней силы в течение периода колебаний
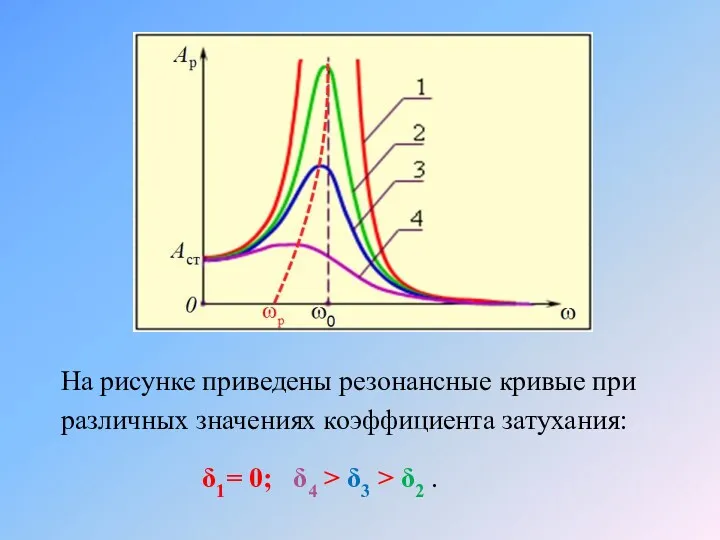
- 44. На рисунке приведены резонансные кривые при различных значениях коэффициента затухания: δ1= 0; δ4 > δ3 >
- 45. У колебательных систем с невысокой добротностью резонансная частота с увеличением коэф-фициента затухания смещается в сторону низких
- 46. Полезное применение резонанса: акустика (усиление звучания музыкальных инструментов; радиотехника и электротехника (выделение полезного сигнала, изме-рение частоты
- 48. Сложение гармонических колебаний одного направления и одинаковой частоты Пусть точка одновременно участвует в двух гармони-ческих колебаниях
- 49. Построим векторные диаграммы этих коле- баний. Так как векторы А1 и А2 вращаются с оди-наковой угловой
- 50. Очевидно, что уравнение результирующего колебания будет где
- 52. Скачать презентацию




































 Насыщенный пар
Насыщенный пар Компенсация реактивной мощности. Потребители реактивной мощности. Лекция 01
Компенсация реактивной мощности. Потребители реактивной мощности. Лекция 01 Ремонт автомобилей. Ремонт корпусных деталей. (Тема 4.3)
Ремонт автомобилей. Ремонт корпусных деталей. (Тема 4.3) Сила упругости. Закон Гука
Сила упругости. Закон Гука Неисправность муфты CVVT впускного вала (приложение 2)
Неисправность муфты CVVT впускного вала (приложение 2) Наблюдение гравитационных волн в эксперименте LIGO
Наблюдение гравитационных волн в эксперименте LIGO Люминесцентные лампы
Люминесцентные лампы Урок физики Движение тела по наклонной плоскости
Урок физики Движение тела по наклонной плоскости Самофокусировка света: физическая картина
Самофокусировка света: физическая картина Күн энергиясын тұрғын үйде қолдану
Күн энергиясын тұрғын үйде қолдану использование интерактивного обордования на роках физики
использование интерактивного обордования на роках физики Источники света. Прямолинейное распространение света.
Источники света. Прямолинейное распространение света. Расчет электрической цепи по закону Кирхгофа
Расчет электрической цепи по закону Кирхгофа Предмет аэродинамики. Лекция 1
Предмет аэродинамики. Лекция 1 Закон сохранения механической энергии
Закон сохранения механической энергии Unusual modes pf transport
Unusual modes pf transport Электромагнетизм и магнитные цепи
Электромагнетизм и магнитные цепи Конденсатор. Электроёмкость
Конденсатор. Электроёмкость Ремонт системы питания КамАЗ 4326
Ремонт системы питания КамАЗ 4326 Методическая разработка урока физики 8 класс. Лабораторная работа № 12 Исследование зависимости угла отражения от угла падения света.
Методическая разработка урока физики 8 класс. Лабораторная работа № 12 Исследование зависимости угла отражения от угла падения света. Опиливание металла
Опиливание металла Биологические мембраны. Биоэлектрогенез
Биологические мембраны. Биоэлектрогенез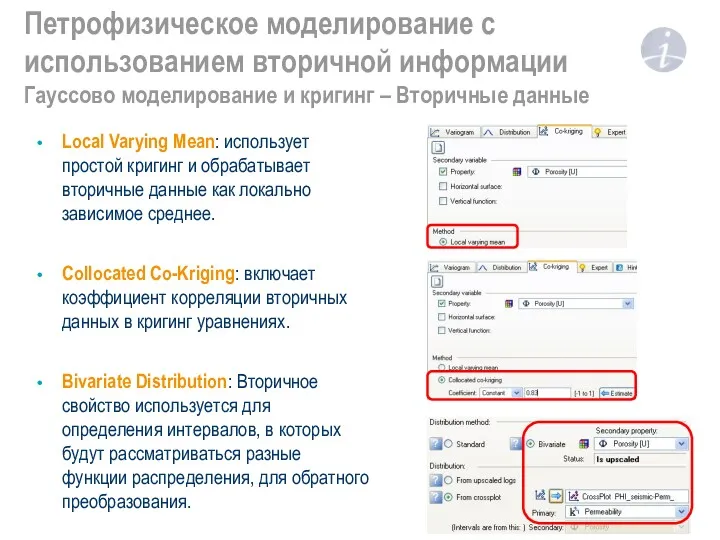 Петрофизическое моделирование с использованием вторичной информации. Гауссово моделирование и кригинг – Вторичные данные
Петрофизическое моделирование с использованием вторичной информации. Гауссово моделирование и кригинг – Вторичные данные Трехфазный переменный ток
Трехфазный переменный ток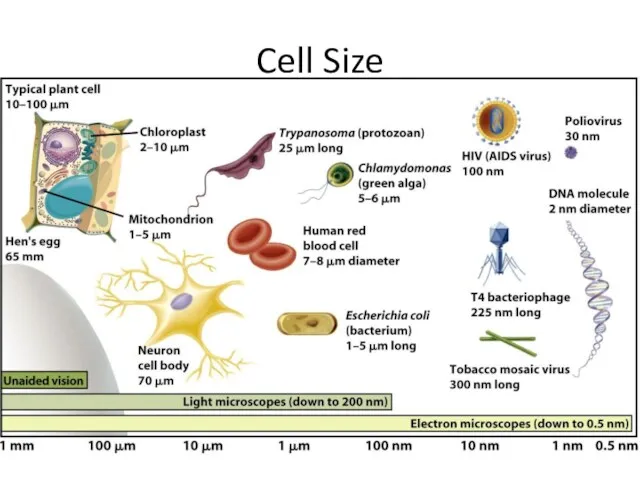 Microscope Measurement
Microscope Measurement Надпровідність. Перспективи та застосування. Надпровідники. Лампа, діод, транзистор. Електричний струм у металах
Надпровідність. Перспективи та застосування. Надпровідники. Лампа, діод, транзистор. Електричний струм у металах Электростатика. Электрические заряды
Электростатика. Электрические заряды урок обобщения по теме Электрические явления 8 класс , презентация
урок обобщения по теме Электрические явления 8 класс , презентация