Содержание
- 2. Рекомендуемая литература Часть 1: Теоретическая механика 1. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Статика, кинематика,
- 3. Содержание Лекция 1. Введение в динамику. Законы и аксиомы динамики материальной точки. Основное уравнение динамики. Дифференциальные
- 4. Содержание Лекция 5. . Относительное движение материальной точки. Силы инерции. Частные случаи движения для различных видов
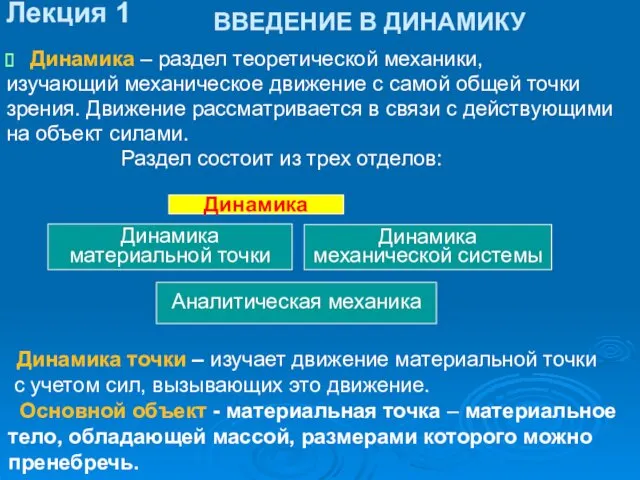
- 5. ВВЕДЕНИЕ В ДИНАМИКУ Динамика – раздел теоретической механики, изучающий механическое движение с самой общей точки зрения.
- 6. Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами взаимодействия,
- 7. Отсюда вытекает: – существует абсолютно неподвижная система отсчета; – время не зависит от движения системы отсчета;
- 8. Сила – величина переменная и зависит от: а) времени - б) положения точки приложения силы -
- 9. 13. ОСНОВНЫЕ ВИДЫ СИЛ Сила тяжести. м./c2 Сила трения скольжения коэффициент трения нормальная реакция. ускорение свободного
- 10. В основе классической механики лежат законы, впервые изложенные И. Ньютоном в работе «Математические начала натуральной философии»
- 11. Закон пропорциональности силы и ускорения (Основное уравнение динамики - II закон Ньютона) – Ускорение, сообщаемое материальной
- 12. Закон равенства действия и противодействия (III закон Ньютона) - Всякому действию соответствует равное по величине и
- 13. Основное уравнение динамики : - соответствует векторному способу задания движения точки. 15. Основное уравнение динамики Основной
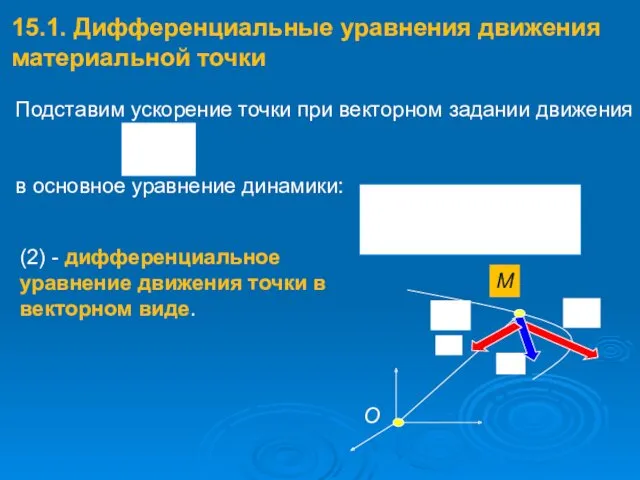
- 14. 15.1. Дифференциальные уравнения движения материальной точки Подставим ускорение точки при векторном задании движения в основное уравнение
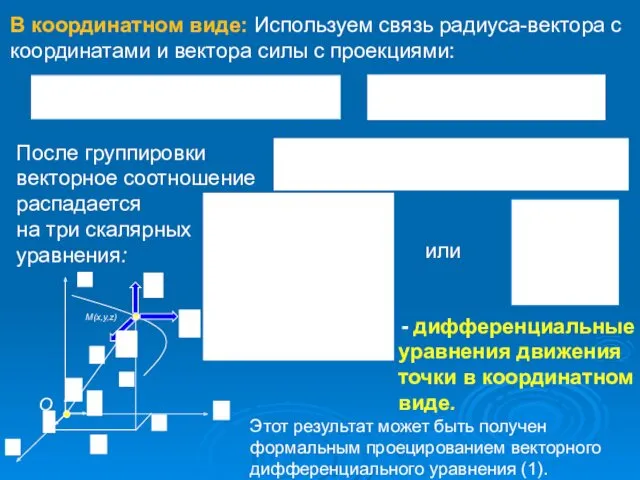
- 15. - дифференциальные уравнения движения точки в координатном виде. Этот результат может быть получен формальным проецированием векторного
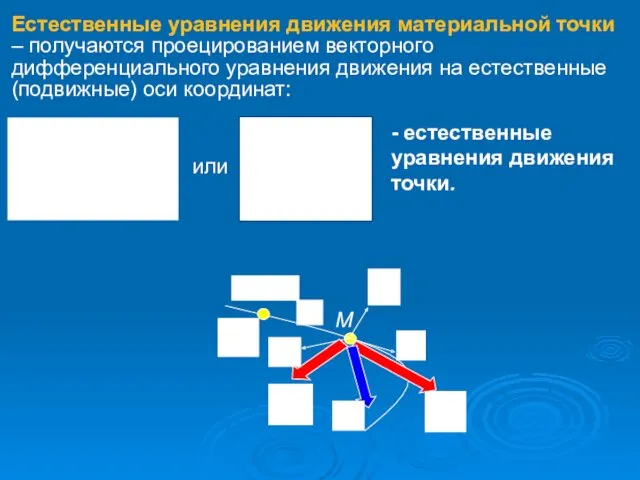
- 16. Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения движения на естественные (подвижные) оси
- 17. Прямая задача: Задано движение (уравнения движения, траектория). Требуется определить силы, под действием которых происходит заданное движение.
- 18. 2. Отбрасываем связь (трос) и заменяем реакцией R. 3. Составляем основное уравнение динамики: Определяем реакцию троса:
- 19. После подстановки найденных значений постоянных получаем: Таким образом, под действием одной и той же системы сил
- 20. 17. Общие указания к решению прямой и обратной задачи. Порядок решения 1. Составление дифференциального уравнения движения:
- 21. 1.2. Изобразить точку в положении, соответствующем произвольному моменту времени (при t > 0) так, чтобы координаты
- 22. 2. Решение дифференциальных уравнений: 2.1. Понизить производную, если уравнение не приводится к каноническому (стандартному) виду. например:
- 23. 2.4. Вычислить неопределенные интегралы в левой и правой частях уравнения, например: Замечание. Вместо вычисления неопределенных интегралов
- 24. 2.5. Выразить скорость через производную координаты по времени, например, и повторить пункты 2.2 -2.4 Замечание. Если
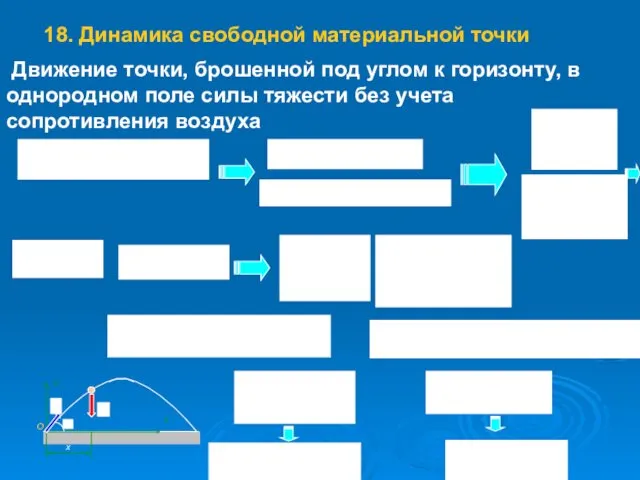
- 25. Движение точки, брошенной под углом к горизонту, в однородном поле силы тяжести без учета сопротивления воздуха
- 26. x 19. Виды колебаний материальной точки 1. Свободные колебания (без учета сопротивления среды). 2. Свободные колебания
- 27. x Данное уравнение является однородным линейным дифференциальным уравнением II порядка, вид решения которого определяется корнями характеристического
- 28. Затухающие колебания материальной точки – колебательное движение материальной точки происходит при наличии восстанавливающей силы и силы
- 29. 20. Относительное движение материальной точки Основное уравнение динамики: Абсолютное ускорение точки: Перенесем слагаемые с переносным и
- 30. Спасибо за внимание!
- 31. Лекция 2 Система материальных точек или механическая система – Совокупность материальных точек или материальных тел, объединяемых
- 32. Лекция 2 В дополнение к ранее существовавшей классификации сил (активные и реактивные силы) вводится новая классификация
- 33. А З В На основании закона действия и противодействия каждой внутренней силе соответствует другая внутренняя сила
- 34. Для описания движения системы в целом вводится геометрическая точка, называемой центром масс, радиус-вектор которой определяется выражением
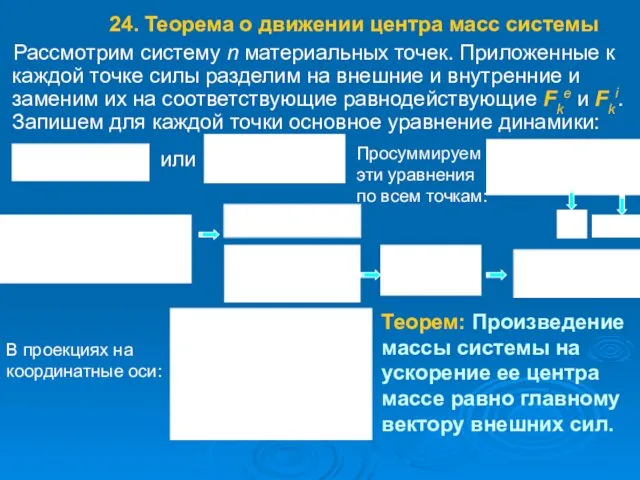
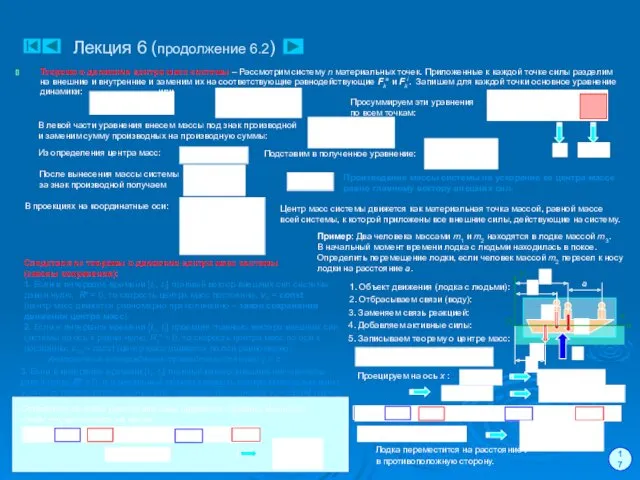
- 35. Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и
- 36. Следствия из теоремы о движении центра масс системы (законы сохранения) 1. Если в интервале времени [t1,
- 37. Мера механического взаимодействия, характеризующая передачу механического движения со стороны действующих на точку сил за данный промежуток
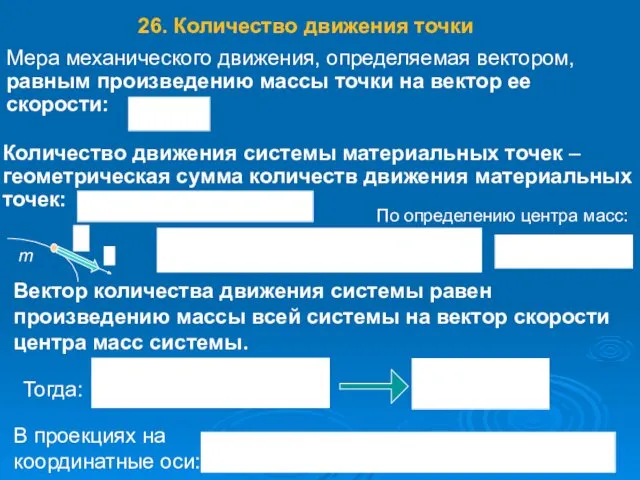
- 38. Мера механического движения, определяемая вектором, равным произведению массы точки на вектор ее скорости: Количество движения системы
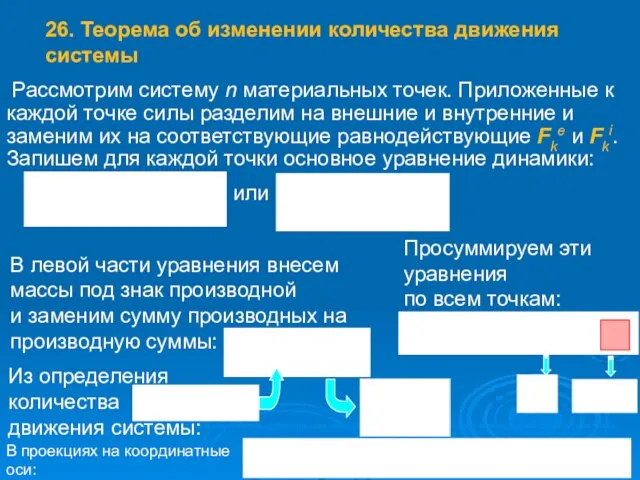
- 39. Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и
- 40. : 1. Если в интервале времени [t1, t2] главный вектор внешних сил системы равен нулю, Re
- 41. Мера механического движения, определяемая вектором, равным векторному произведению радиуса-вектора материальной точки на вектор ее количества движения:
- 42. Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и
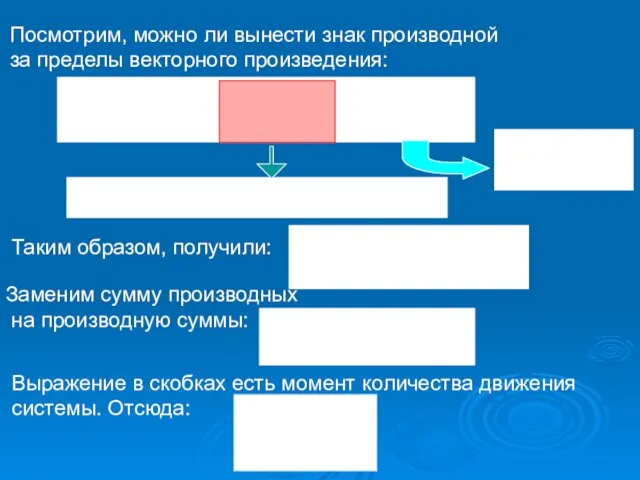
- 43. Заменим сумму производных на производную суммы: Выражение в скобках есть момент количества движения системы. Отсюда: Посмотрим,
- 44. Теорема: Производная вектора момента количества движения системы относительно некоторого центра по времени равна главному моменту внешних
- 45. Если в интервале времени [t1, t2] вектор главного момента внешних сил системы относительно некоторого центра равен
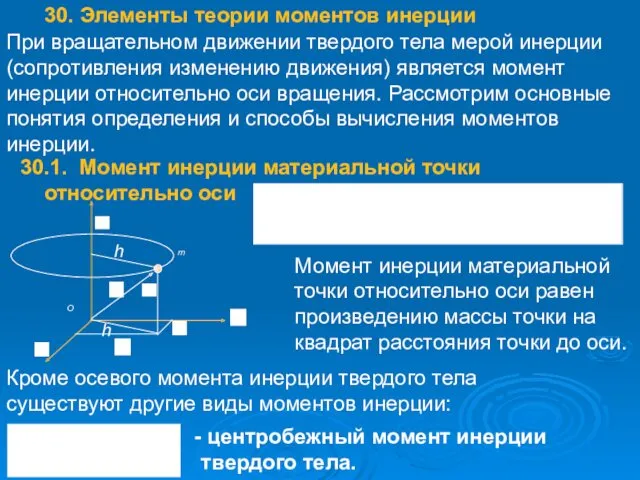
- 46. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси.
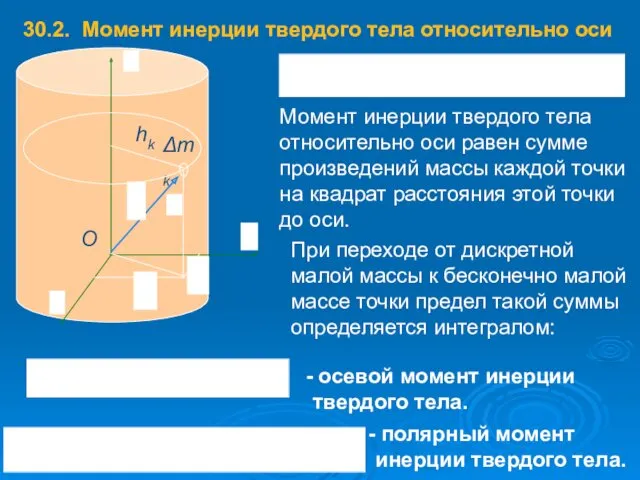
- 47. 30.2. Момент инерции твердого тела относительно оси Момент инерции твердого тела относительно оси равен сумме произведений
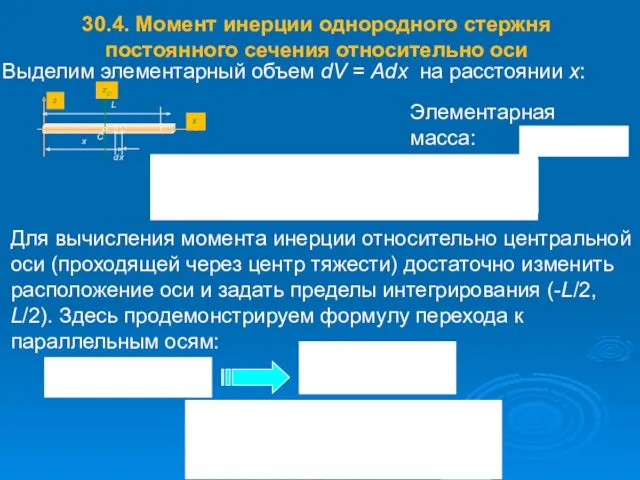
- 48. 30.4. Момент инерции однородного стержня постоянного сечения относительно оси x z L Выделим элементарный объем dV
- 49. 30.5. Момент инерции однородного сплошного цилиндра относительно оси симметрии Выделим элементарный объем: dV = 2πrdrH (тонкий
- 50. 31. Кинетический момент твердого тела Выделим дискретный малый объем массы Δmi : Или переходя к бесконечно
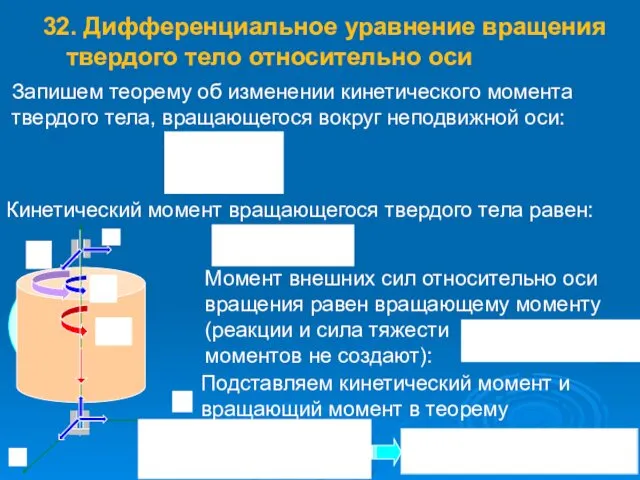
- 51. 32. Дифференциальное уравнение вращения твердого тело относительно оси Запишем теорему об изменении кинетического момента твердого тела,
- 52. Гироскоп – твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек которой неподвижна. Свободный гироскоп
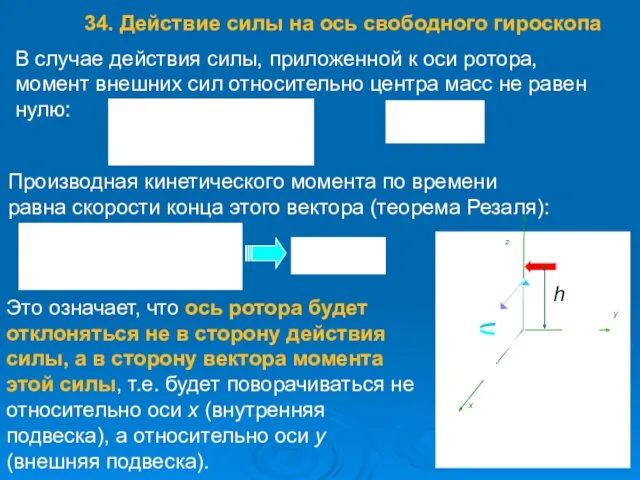
- 53. Основное допущение приближенной (элементарной) теории гироскопа – вектор момента количества движения (кинетический момент) ротора считается направленным
- 54. В случае действия силы, приложенной к оси ротора, момент внешних сил относительно центра масс не равен
- 55. При прекращении действия силы ось ротора останется в неизменном положении, соответствующем последнему моменту времени действия силы,
- 56. Спасибо за внимание!
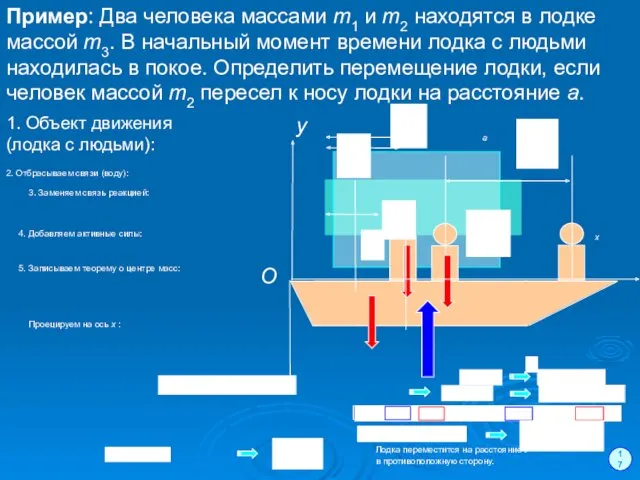
- 57. 17 Пример: Два человека массами m1 и m2 находятся в лодке массой m3. В начальный момент
- 58. Лекция 6 (продолжение 6.2) 17 Теорема о движении центра масс системы – Рассмотрим систему n материальных
- 59. Лекция 8 (продолжение 8.2) 22 Момент инерции однородного стержня постоянного сечения относительно оси: x z L
- 61. Скачать презентацию



























![: 1. Если в интервале времени [t1, t2] главный вектор](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/91647/slide-39.jpg)



![Если в интервале времени [t1, t2] вектор главного момента внешних](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/91647/slide-44.jpg)







 Задачи. Конвективный теплообмен
Задачи. Конвективный теплообмен Определение давления тела на опору
Определение давления тела на опору Устройство железнодорожных вагонов
Устройство железнодорожных вагонов Компрессоры. Общие положения
Компрессоры. Общие положения Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление
Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление Снегоходы
Снегоходы Восстанавливающие моменты
Восстанавливающие моменты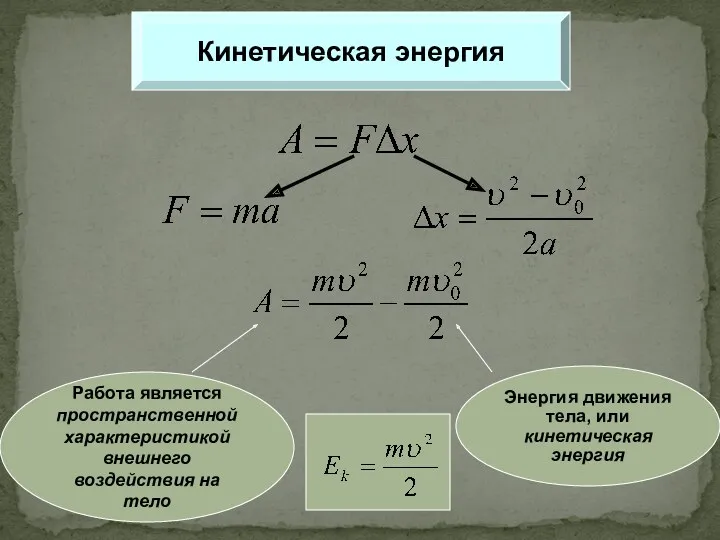 Кинетическая энергия
Кинетическая энергия Робота електричного струму
Робота електричного струму Зубчатая передача электровоза ВЛ85
Зубчатая передача электровоза ВЛ85 Заломлення світла на межі поділу двох середовищ. Закон заломлення світла
Заломлення світла на межі поділу двох середовищ. Закон заломлення світла Удельная теплота плавления
Удельная теплота плавления Системы секретной связи. Засекречивание сообщений
Системы секретной связи. Засекречивание сообщений Эксперимент на уроках физики в основной школе как средство формирования УУД
Эксперимент на уроках физики в основной школе как средство формирования УУД Электрооборудование автомобилей. Системы автоматического управления тормозами. (Урок 14)
Электрооборудование автомобилей. Системы автоматического управления тормозами. (Урок 14) Хроматография. Основы метода и ключевые параметры
Хроматография. Основы метода и ключевые параметры Контрольно-измерительные приборы
Контрольно-измерительные приборы Профилирование кулачков. Кинематика кулачковых механизмов. (Лекция 19)
Профилирование кулачков. Кинематика кулачковых механизмов. (Лекция 19) Выступление на заседании МО учителей естественно-математического цикла Формирование УУД учащихся 7 класса на уроках физики
Выступление на заседании МО учителей естественно-математического цикла Формирование УУД учащихся 7 класса на уроках физики Задачи на определение магнитного поля
Задачи на определение магнитного поля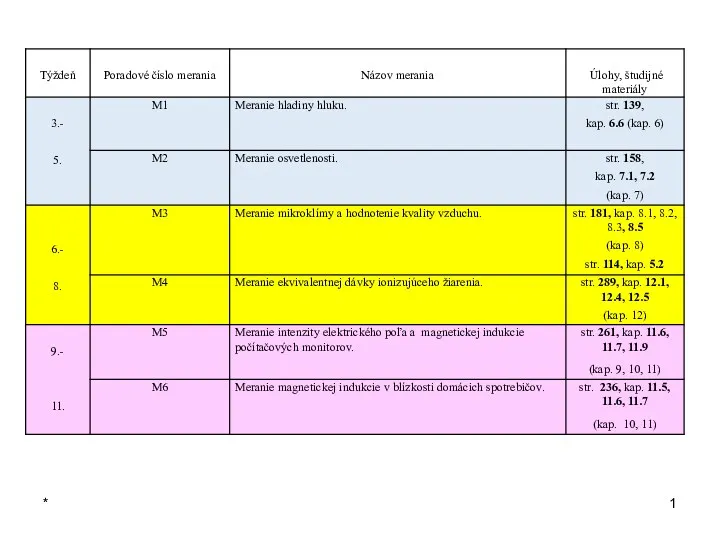 Úlohy merania mikroklímy
Úlohy merania mikroklímy Электрический ток в жидкостях
Электрический ток в жидкостях Влияние теплопроводности различных утеплителей на защитные свойства одежды
Влияние теплопроводности различных утеплителей на защитные свойства одежды Плазмалық технологиялардың физикалық негіздері
Плазмалық технологиялардың физикалық негіздері Лекция 9. Мезонные теории ядерных сил
Лекция 9. Мезонные теории ядерных сил Основи процесів горіння. Полум’я. Процеси, що відбуваються у полум’ї. (Розділ 1.1.2)
Основи процесів горіння. Полум’я. Процеси, що відбуваються у полум’ї. (Розділ 1.1.2) Кинематика
Кинематика Презентация к уроку Колебания
Презентация к уроку Колебания