Содержание
- 2. Цели и вопросы занятия Изучить компоненты математических моделей систем распределения информации и их условные обозначения, используемые
- 3. 1. 1. Зотов В. М. Основы теории распределения информации. – СПб.: ВАС, 2013 г. 1. Зотов
- 4. 1. 4 1.Компоненты математических моделей систем распределения информации
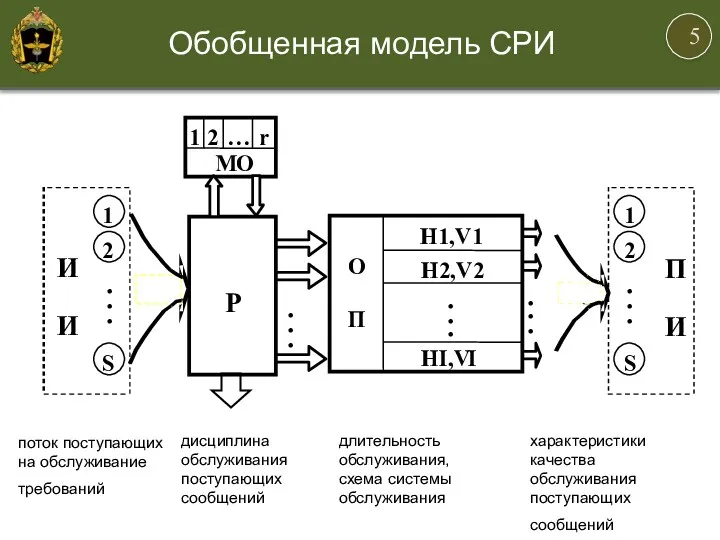
- 5. Обобщенная модель СРИ поток поступающих на обслуживание требований дисциплина обслуживания поступающих сообщений длительность обслуживания, схема системы
- 6. Вероятность события есть численная мера степени объективной возможности этого события. P(A) = n / m Вероятность
- 7. Случайные величины могут быть двух типов: дискретные (прерывные), принимающие только отделённые друг от друга значения, которые
- 8. Математическое описание случайных величин предполагает задание закона распределения, устанавливающего соответствие между значениями случайной величины и вероятностью
- 9. а) аналитически в виде математического выражения, отражающего зависимость вероятности от значения случайной величины: б) таблично в
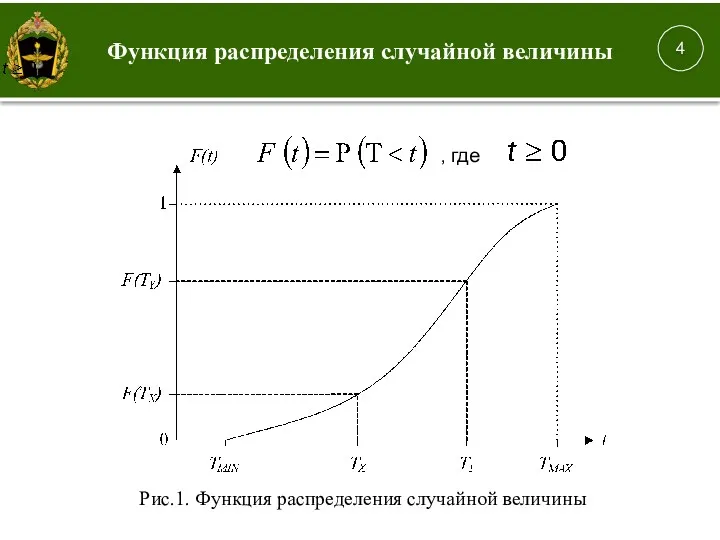
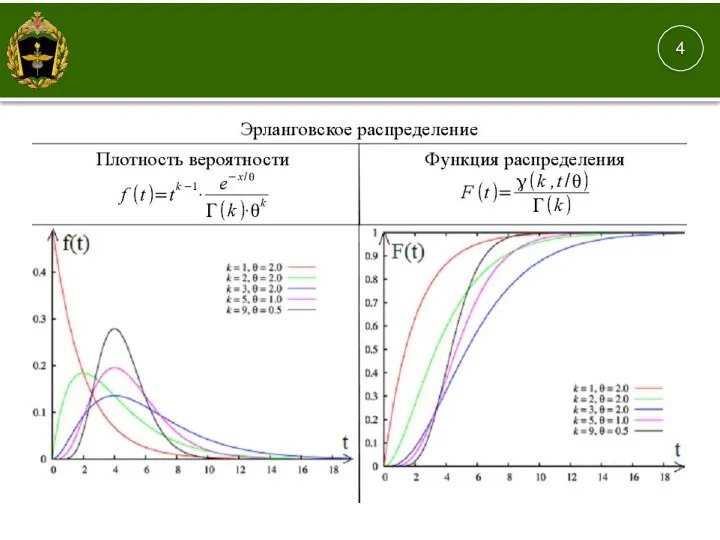
- 10. Функция распределения вероятностей F(x) случайной величины X представляет собой вероятность того, что случайная величина X примет
- 11. Функция распределения случайной величины 4 , ; , где Рис.1. Функция распределения случайной величины
- 12. среднее значение, около которого группируются возможные значения случайной величины; степень разбросанности этих значений относительно среднего; асимметрию
- 13. Начальный момент s-го порядка Первый начальный момент α1[X ] случайной величины Х называется математическим ожиданием или
- 14. Центральный момент s-го порядка Разность между значениями случайной величины и ее математическим ожиданием (X – М[X])
- 15. Дисперсия Второй центральный момент называется дисперсией случайной величины и обозначается D[X]= β2[X]. Среднее квадратическое отклонение (стандартное
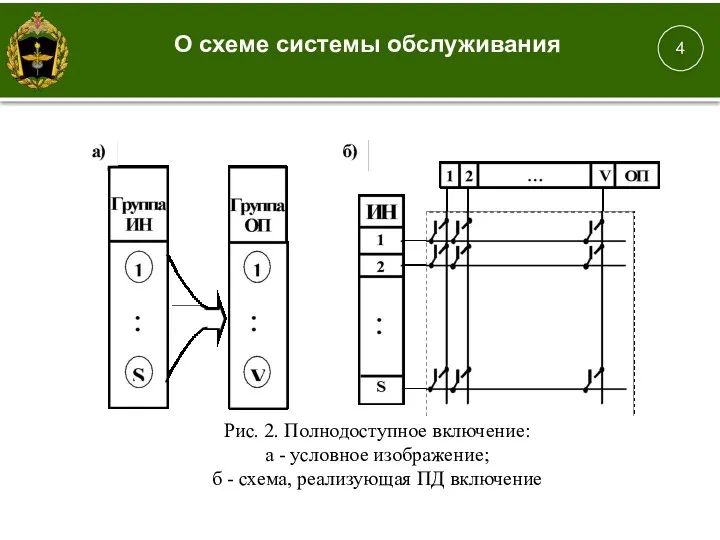
- 16. 1. 4 Рис. 2. Полнодоступное включение: а - условное изображение; б - схема, реализующая ПД включение
- 17. 4 О дисциплине обслуживания - способы обслуживания вызовов (без потерь, с потерями, с ожиданием) порядок обслуживания
- 18. 1. 4 О характеристиках качества обслуживания p (tож > 0);
- 19. 1. 4 2.Классификация Кендалла-Башарина
- 20. 1. 4 Первый символ условной записи обозначает функцию распределения промежутков между вызовами, второй - функцию распределения
- 21. 1. 4
- 22. 1. 4
- 24. Скачать презентацию









![Начальный момент s-го порядка Первый начальный момент α1[X ] случайной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/257486/slide-12.jpg)






 iOS Developer
iOS Developer Microstrategy visualization guidelines
Microstrategy visualization guidelines Розробка автоматизованої комп’ютерної системи обліку ресурсів і випуску продукції
Розробка автоматизованої комп’ютерної системи обліку ресурсів і випуску продукції Безопасность детей в сети интернет
Безопасность детей в сети интернет Электронные информационные ресурсы культуры и искусств
Электронные информационные ресурсы культуры и искусств Мәліметтер қорымен жұмыс
Мәліметтер қорымен жұмыс Массивы. Описание массивов
Массивы. Описание массивов Raqamli iqtisodiyotning rivojlanish bosqichlari
Raqamli iqtisodiyotning rivojlanish bosqichlari Мультимедийные презентации на уроке истории
Мультимедийные презентации на уроке истории Представление информации в форме таблиц. Структура таблицы. Информатика. 5 класс
Представление информации в форме таблиц. Структура таблицы. Информатика. 5 класс Понятие модели и моделирования. Цели и принципы моделирования
Понятие модели и моделирования. Цели и принципы моделирования Закреплеие знания разветвляющихся программ
Закреплеие знания разветвляющихся программ Subversion
Subversion Building the user interface by using HTML5. Text, graphics and media
Building the user interface by using HTML5. Text, graphics and media Поисковые системы интернета
Поисковые системы интернета Файлы и файловая система
Файлы и файловая система Основи Java Script. Масиви
Основи Java Script. Масиви Логические основы компьютеров. Задания
Логические основы компьютеров. Задания Статическая маршрутизация, RIP, NAT ALL
Статическая маршрутизация, RIP, NAT ALL Acronis Backup 12.5. Современная система защиты данных для предприятий любого размера
Acronis Backup 12.5. Современная система защиты данных для предприятий любого размера Инструкция по созданию интерактивных физкультминуток
Инструкция по созданию интерактивных физкультминуток Текстовый процессор Microsoft Office Word
Текстовый процессор Microsoft Office Word Присоединение Крыма к Российской Федерации: контент-анализ российских печатных СМИ
Присоединение Крыма к Российской Федерации: контент-анализ российских печатных СМИ Системы счисления, основные понятия математической логики
Системы счисления, основные понятия математической логики Решение задач с использованием условного оператора
Решение задач с использованием условного оператора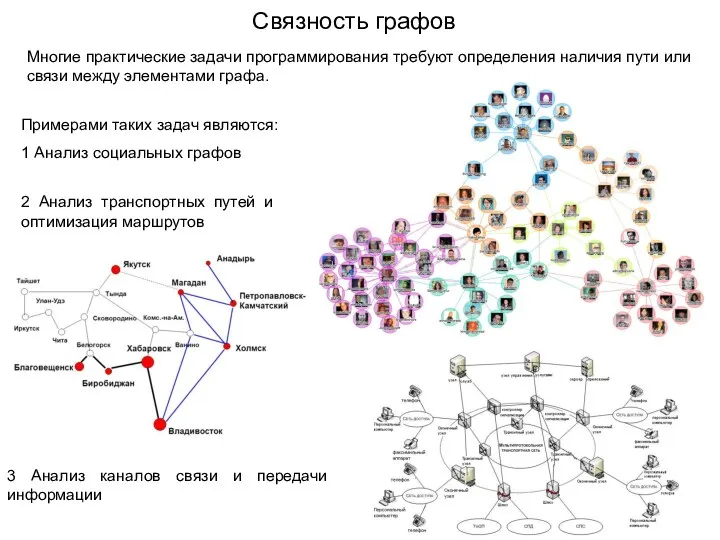 Связность графов
Связность графов Кодирование информации. Числовая информация. 2 класс
Кодирование информации. Числовая информация. 2 класс Разработка презентации
Разработка презентации