Содержание
- 2. Философ Платон (428—347). Сочинения Платона содержат важный вклад в развитие философской логики. Платон ставит три вопроса:
- 3. Логика Аристотеля, в частности его теория силлогизма, имела огромное влияние на западную мысль. Его труды по
- 4. Немецкий ученый Готфрид Лейбниц (1646 - 1716) заложил основы математической логики. Он пытался построить первые логические
- 5. Англичанин Джордж Буль (1815 - 1864) на фундаменте, заложенном Лейбницем, создал новую область науки - математическую
- 6. В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Высказывание можно
- 7. ЛОГИЧЕСКИЕ ОПЕРАЦИИ Отрицание (инверсия) Обозначение: НЕ А, ¬А, А= {множество учеников 10 А класса} = {множество
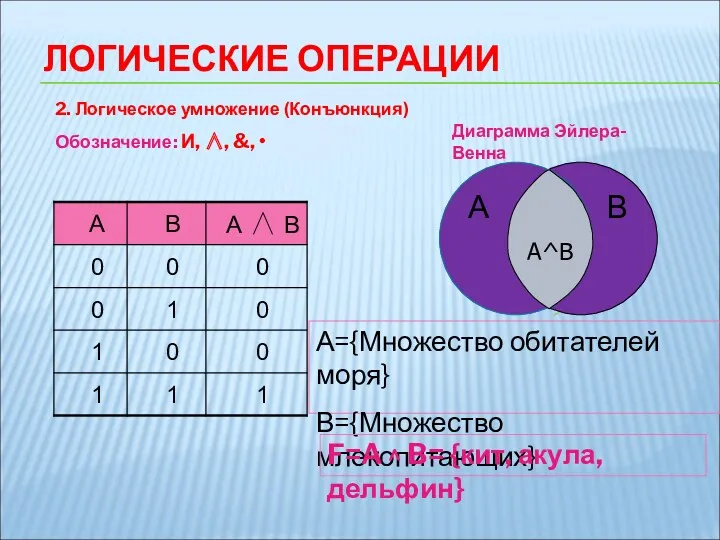
- 8. 2. Логическое умножение (Конъюнкция) Обозначение: И, ∧, &, • ЛОГИЧЕСКИЕ ОПЕРАЦИИ Диаграмма Эйлера-Венна А={Множество обитателей моря}
- 9. ЛОГИЧЕСКИЕ ОПЕРАЦИИ 3. Логическое сложение (Дизъюнкция) Обозначение: ИЛИ,∨, +, | А∨В А={Множество учеников 10 А класса}
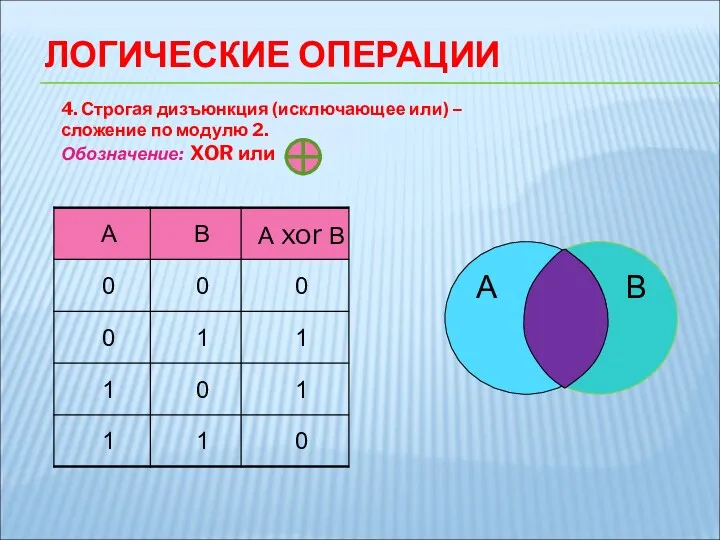
- 10. 4. Строгая дизъюнкция (исключающее или) – сложение по модулю 2. Обозначение: XOR или + ЛОГИЧЕСКИЕ ОПЕРАЦИИ
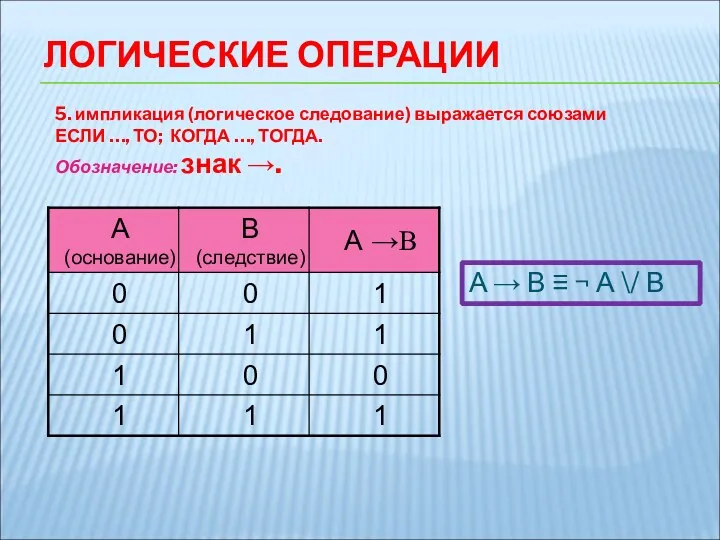
- 11. 5. импликация (логическое следование) выражается союзами ЕСЛИ …, ТО; КОГДА …, ТОГДА. Обозначение: знак →. ЛОГИЧЕСКИЕ
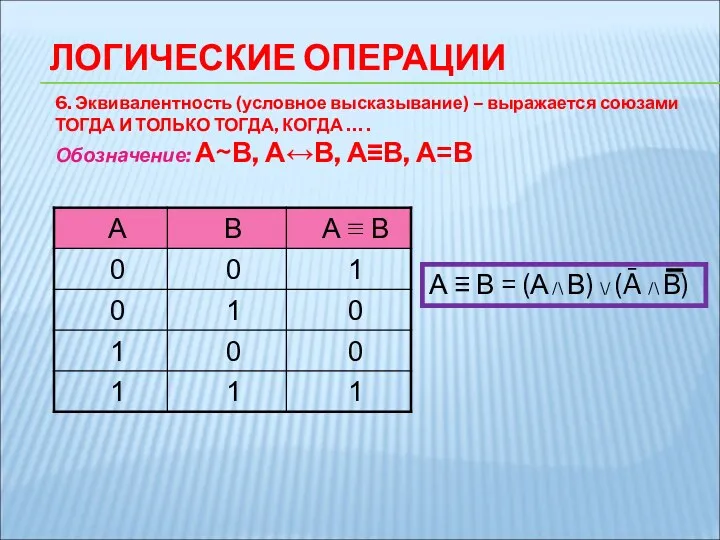
- 12. 6. Эквивалентность (условное высказывание) – выражается союзами ТОГДА И ТОЛЬКО ТОГДА, КОГДА … . Обозначение: А~В,
- 13. Приоритет логических операций: () Операции в скобках НЕ Отрицание И логическое умножение ИЛИ Логическое сложение →
- 14. ОСНОВЫ ЛОГИКИ Решение задач ЕГЭ
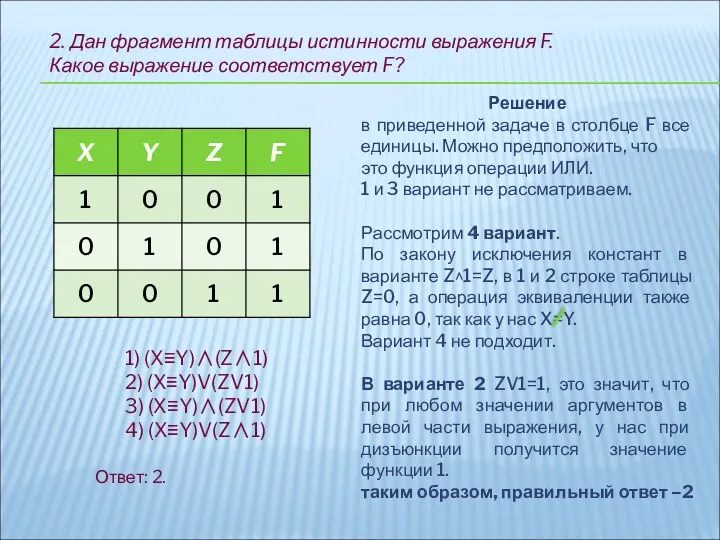
- 15. 2. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F? Ответ: 2. 1) (X≡Y)∧(Z∧1) 2)
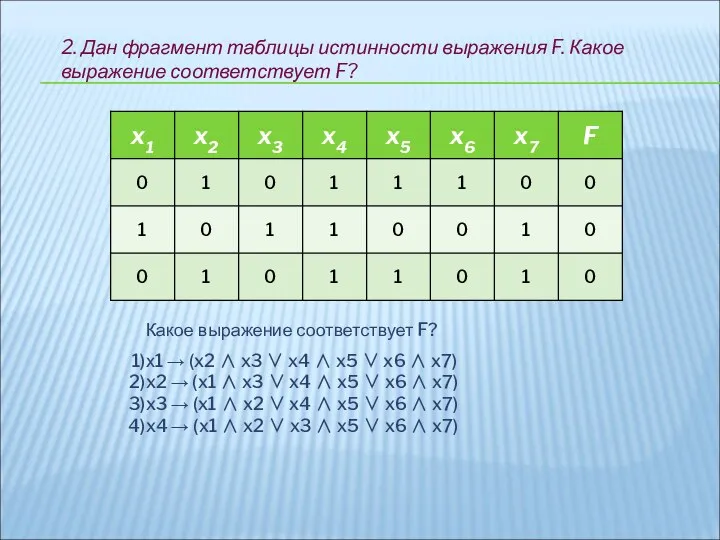
- 16. 2. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F? Какое выражение соответствует F? х1
- 17. 2. решение Логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна,
- 18. 2. Дано логическое выражение, зависящее от 4 логических переменных: (x1 ∧ ¬x2 ) ∧ (x2 ∨
- 19. 18. определите наибольшее число X, при котором истинно логическое высказывание: F = ((X *Х – 45>
- 20. 18. Для какого имени истинно высказывание: (первая буква согласная → вторая буква имени согласная) ∧ (предпоследняя
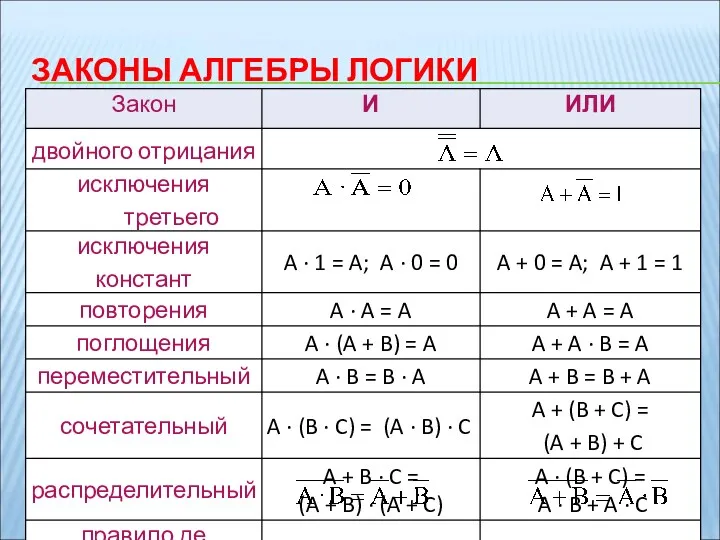
- 21. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
- 22. Для упрощения нахождения значений логических выражений их преобразуют с помощью законов алгебры логики (минимизируют). Форма, которой
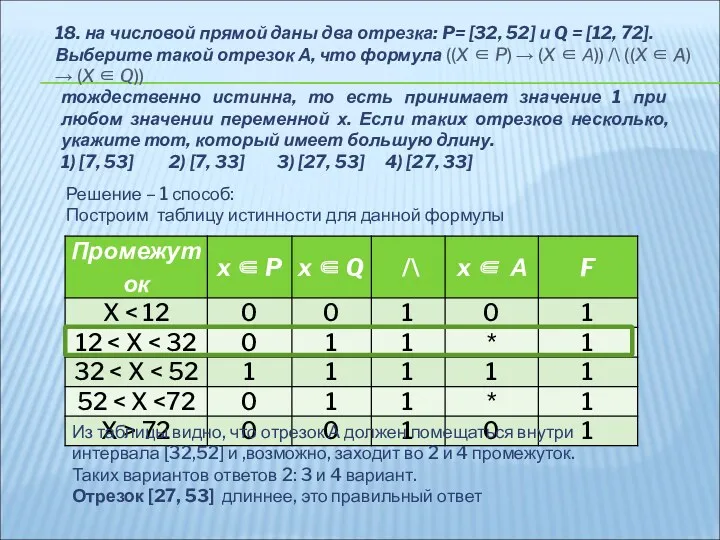
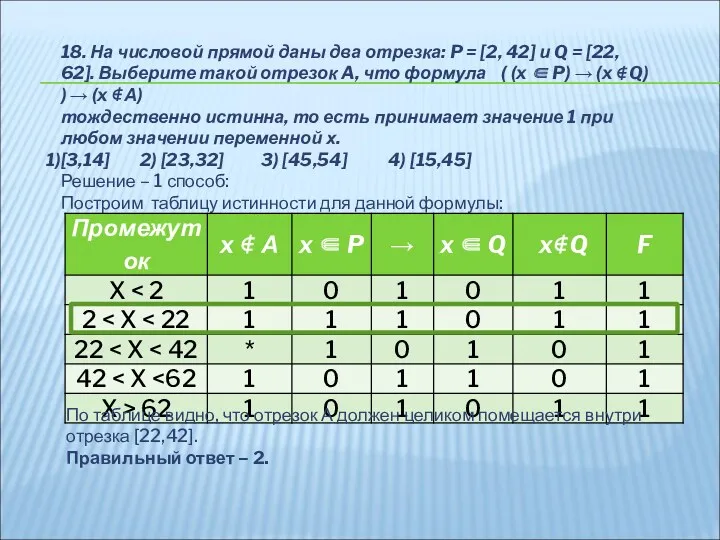
- 23. тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько,
- 24. 18. Решение – способ 2 Преобразуем выражение: ( (x ∈ P) → (x ∈ А) )
- 25. 18. На числовой прямой даны два отрезка: P = [2, 42] и Q = [22, 62].
- 26. 18. Решение – способ 2 Преобразуем выражение ( (x ∈ P) → (x ∉ Q) )
- 27. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Логические выражения и операции
- 28. 1 задание: Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, Y,
- 29. 3 задание: Дан фрагмент таблицы истинности выражения F: Какое выражение соответствует F? 1) х1∨х2∨х3∨¬х4∨ ¬х5 2)
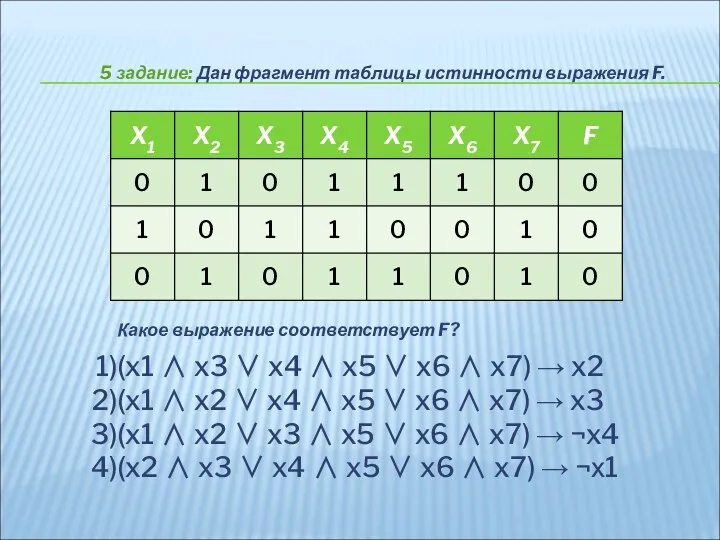
- 30. 5 задание: Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F? (x1 ∧ x3 ∨
- 31. 6 задание: Для какого имени истинно высказывание: (первая буква согласная → последняя буква имени согласная) V
- 32. Задание 9: На числовой прямой даны два отрезка: P = [2, 10] и Q = [6,
- 34. Скачать презентацию





















 Робота з даними
Робота з даними Методы теории нечетких систем
Методы теории нечетких систем Разработка SATA - IO-link контроллера с программными интерфейсами Legacy и AHCI
Разработка SATA - IO-link контроллера с программными интерфейсами Legacy и AHCI Кодирование графической информации
Кодирование графической информации Приложения Java
Приложения Java ИКТО-2014
ИКТО-2014 Разработка компьютерной презентации Проект загородного дома
Разработка компьютерной презентации Проект загородного дома Встраивание музыки в документы
Встраивание музыки в документы Компьютерные вирусы
Компьютерные вирусы Информационная безопасность
Информационная безопасность Интерфейс программы подготовки презентаций
Интерфейс программы подготовки презентаций Створення програмованих проєктів
Створення програмованих проєктів Using Internet
Using Internet Ппрограммное обеспечение KoBo Toolbox
Ппрограммное обеспечение KoBo Toolbox Вредоносные и антивирусные программы. Компьютерные черви и защита от них
Вредоносные и антивирусные программы. Компьютерные черви и защита от них Windows Xp
Windows Xp Worldwide system of integrated computer networks for storing and transmitting information
Worldwide system of integrated computer networks for storing and transmitting information Презентация к уроку по теме: Зоопарк
Презентация к уроку по теме: Зоопарк Сущность и виды электронных денег. Криптовалюты
Сущность и виды электронных денег. Криптовалюты DVC - система контроля версий для дата-сетов и моделей искусственных нейронных сетей.(2)
DVC - система контроля версий для дата-сетов и моделей искусственных нейронных сетей.(2) Язык программирования Pascal. Линейные алгоритмы
Язык программирования Pascal. Линейные алгоритмы SSD8: Networks and Distributed Computing
SSD8: Networks and Distributed Computing Маршрутизаторы
Маршрутизаторы Использование мультимедийных технологий на уроках
Использование мультимедийных технологий на уроках Поисковая система Bing
Поисковая система Bing Математичні функцій в С++
Математичні функцій в С++ Кодировани и обработка е звуковой информации
Кодировани и обработка е звуковой информации Язык релейных диаграмм(LD)
Язык релейных диаграмм(LD)