Содержание
- 2. Вероятностный подход Приведите примеры уменьшения неопределенности знаний после получения информации о произошедшем событии. В чем состоит
- 3. Равновероятные события 1 бит – единица количества информации величина, уменьшающая неопределенность знаний в два раза. N
- 4. ВЕРОЯТНОСТНЫЙ ПОДХОД Клод Э́лвуд Ше́ннон 30.04.1916 - 24 февраля 2001 американский математик и электротехник, один из
- 5. Формула Шеннона I - количество информации; N - количество возможных событий; рi - вероятность i-го события
- 6. Формула Шеннона Для событий с равной вероятностью (рi=1/N) количество информации рассчитывается по формуле:
- 7. Вероятностный подход Количественная зависимость между вероятностью события (р) и количеством информации в сообщении о нем (i)
- 8. Задача В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое
- 9. Решение рб = 10/100 = 0,1; рк = 20/100 = 0,2; рс = 30/100 = 0,3;
- 10. Задача В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Определите количество информации
- 11. Решение Обозначим рч - вероятность попадания черного шара, рб - вероятность попадания белого шара. рч =
- 12. Вероятностный подход Чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
- 13. Домашнее задание Выучить основные определения и формулы п.2.4 Задания 2.4 – 2.5 (стр. 82)
- 14. Дополнительная задача В пруду живут 8000 карасей, 2000 щук и 40000 пескарей. Определите количество информации при
- 16. Скачать презентацию













 Руководство по написанию материалов для журнала Популярная механика
Руководство по написанию материалов для журнала Популярная механика Презентация Действия с информацией, 5 класс
Презентация Действия с информацией, 5 класс Exception. Java Core
Exception. Java Core 9 класс. Основы программирования
9 класс. Основы программирования Массивы. Паскаль. 9 класс
Массивы. Паскаль. 9 класс Парсинг HTML. Краткий обзор технологий для понимания сбора и обработки данных
Парсинг HTML. Краткий обзор технологий для понимания сбора и обработки данных Профессиональные стандарты в области ИТ
Профессиональные стандарты в области ИТ Математические и инструментальные методы в экономике
Математические и инструментальные методы в экономике Регистрация ККТ через личный кабинет ФНС
Регистрация ККТ через личный кабинет ФНС Работа с программой PowerPoint
Работа с программой PowerPoint Медиабезопасность в образовании
Медиабезопасность в образовании Методы и технологии искусственного интеллекта
Методы и технологии искусственного интеллекта Database. Database management system MySQL
Database. Database management system MySQL Серверная разработка ПО. Лекция 5
Серверная разработка ПО. Лекция 5 Ввод информации в память компьютера. Устройства ввода информации. Клавиатура. Информатика. 5 класс
Ввод информации в память компьютера. Устройства ввода информации. Клавиатура. Информатика. 5 класс Рекурсивные функции. Язык С++
Рекурсивные функции. Язык С++ Форматирование текста (разбиение на колонки) в текстовом процессоре WORD.
Форматирование текста (разбиение на колонки) в текстовом процессоре WORD. Тестовые задания для проведения итоговой аттестации
Тестовые задания для проведения итоговой аттестации IPMI Email Alert translation
IPMI Email Alert translation вычисления в MS Excel
вычисления в MS Excel Глобальная сеть - Интернет
Глобальная сеть - Интернет Интеллектуальная игра для обучающихся 8-10 лет
Интеллектуальная игра для обучающихся 8-10 лет Программирование на ЯВУ Pascal
Программирование на ЯВУ Pascal Подпрограммы в языке Pascal
Подпрограммы в языке Pascal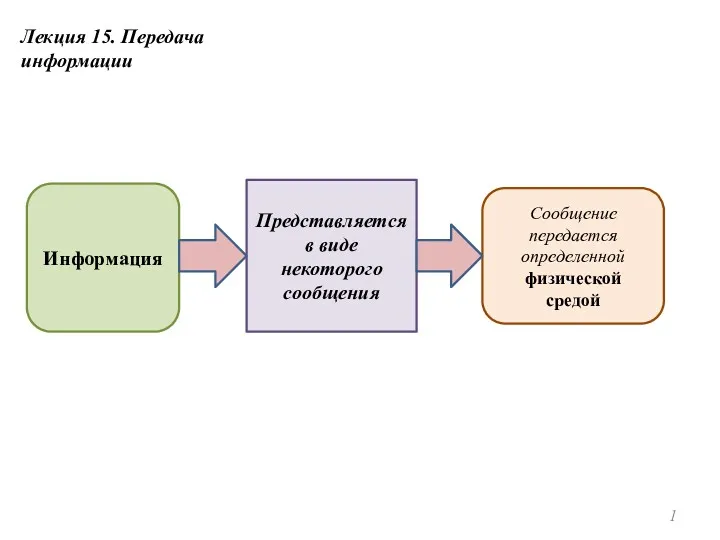 Передача информации
Передача информации Устройства ввода и вывода информации
Устройства ввода и вывода информации Операциялық жүйелер
Операциялық жүйелер Интернет вещей
Интернет вещей